APPLICATION OF LOGARITHMIC AND EXPONENTIAL FUNCTIONS
There are numerous disciplines in which the exponential and logarithmic function are applicable, two of which are compound interest and depreciation.
Compound interest
The compound amount A of a principle P and interest at the end of n years at the rate r compound annually, is given by An = P(1 + r)n
Note:
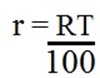where,
T – is the compounding period
R- is the rate of interest growth
The compound interest can be derived in a number of ways, In general if P is the principle, R is the rate (%) of interest I, then the amount A after T period in years will be,
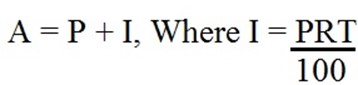
For year 1; It will be,
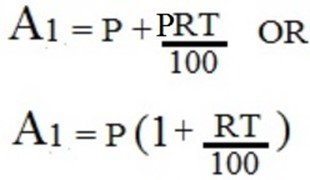…………………….(i)
For year 2: It will be,
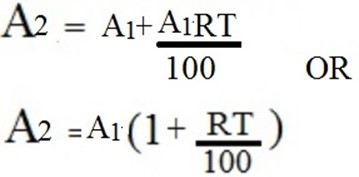………………….(ii)
Substituting eqn (i) into (ii)
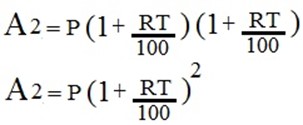
If the acceleration is made up to year n, the total amount An will generally be given as,
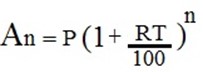
Example;
Suppose TZs 2000/= is invested for 5 years at the rate of 2% compounded annually.
a) Find the compound amount, S
B) Find the compound interest, I
Solution
a) From,
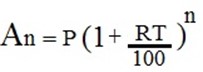
Where, P = 2000, r = 2%, n = 5
Then, S = 2000(1 + 0.02)5
= 2000(1.02)5 = 2208.16
∴ The compound Amount is TZs, 2208.16
b) Compound Interest,
I = S – P
I = 2208.16 – 2000
I = 208.16
∴ The compound interest is TZs, 208.16
DEPRECIATION
Depreciation is a reduction in the value of an asset with time passage, as a result of wear and tear, age or obsolescence.
Example
A phone costs TZs 40000/=. Then phone loses 10% of its value during the first year and 25% of its value during the second year. It means that in year 1, the depreciation will be,
10% of TZs 40000.
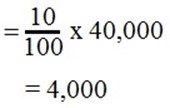
So, the phone will be TZs, 40000 – 4000 = 36000
= TZs 36000/=
In year 2, the depreciation will be 25% of 36000/=
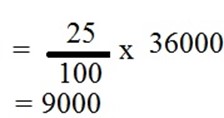
The phone value will be 36000 – 9000 = 27,000.
Therefore after 2 years, the phone worth TZs 27,000/=
If an asset depreciates at R% per annum, then from the preset or initial value P its value in the year 1 will be,
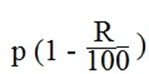
Each succession year the value is multiplied by the same factor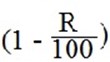 
, and therefore after t years the future value V will be,
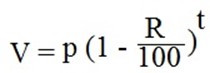
This is the depreciation formula, where V is the future, R the rate of depreciation , P the present or initial value and t is the number of years.
Question
A laptop purchased for TZs 600,000. depreciation at a rate of 30% per annum. After how many years will the machine have a value of TZs 400,000?
USE OF EXPONENTIAL FUNCTIONS FOR COMPOUND INTEREST PROBLEMS
The compound interest problem can be described by using the exponential function. Recall the formula for compound interest , the amount A after t years with a principle P and per annum interest rate r, compound n times per year is
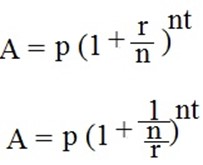
If we let
implying that n = Mr then by substitution we have,
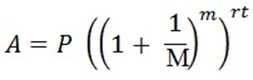
As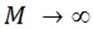 
, then interest will be compounded continuously and then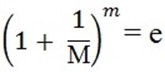 
This implies that as the interest gets compounded continuously, the amount A after t years will be exponential function with a continuously compounding interest growing exponentially given by,
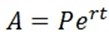
Where, P = Principle amount
r = annual interest rate
t = number of years.