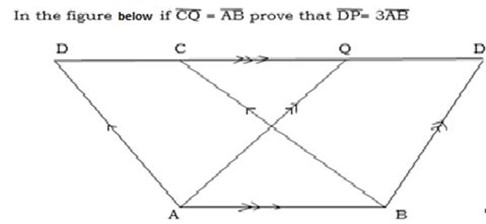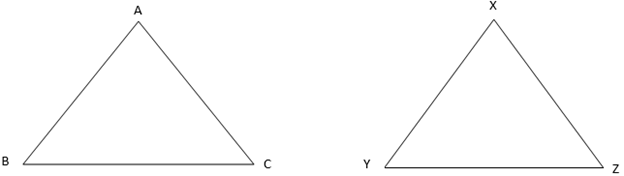
The triangles above are drawn such that
C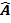 B= Z
B= Z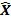 Y
Y
A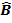 C=X
C=X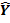 Z
Z
B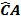 =Y
=Y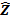 X
X
Corresponding sides in the triangles are those sides which are opposite to the equal angles i.e.

If the corresponding sides are equal i.e.

In general, polygons are congruent if corresponding sides and corresponding angles are equal.
The symbol for congruence is 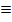
Congruence of triangles
Case 1: Given three sides
Two triangles are congruent if the three pairs of corresponding sides are such that the sides in each pair are equal.
Consider the triangles below:
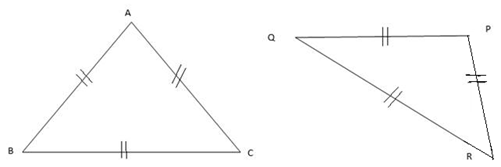
Note: SSS- is an abbreviation of side- side- side
Examples :
Solution

Construction of A is joined C

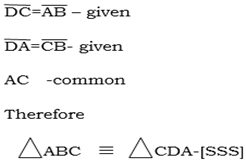

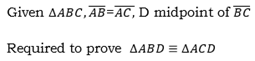
Construction; A joined to D

Case 2; Given two sides and the included angle (SAS)
Two triangles are congruent if two pairs of corresponding sides are such that the sides in each pair are equal and the angles included between the given sides in each triangle are equal.
Examples
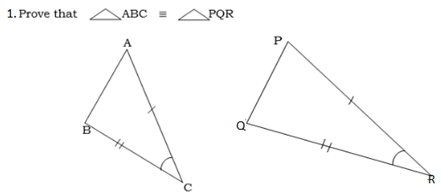
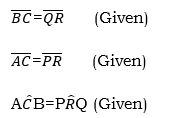
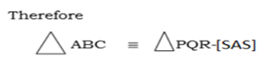

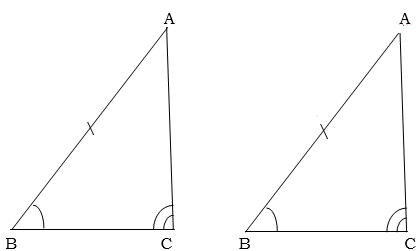
Case 3; Given two angles and a corresponding side
Two triangles are congruent if two pairs of corresponding angles are such that the angles in each triangle are equal.
Example
Solution
Case 4: Given that a right angle hypotenuse and one side (RHS)
The right angled triangles are congruent if the hypotenuse and a side of one triangle are respectively equal to the hypotenuse and side of another triangle
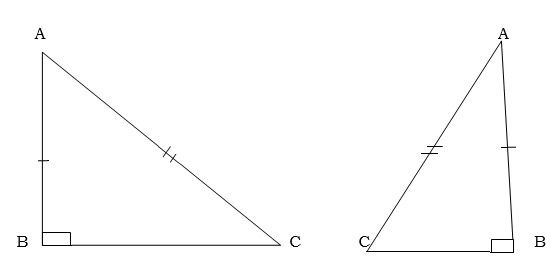
Example:
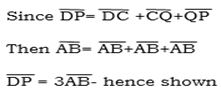
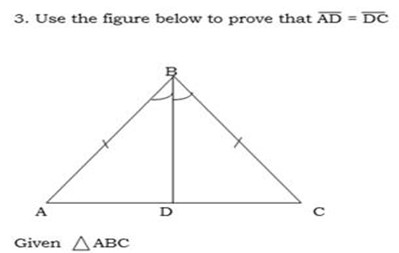
Use the figure below to prove that
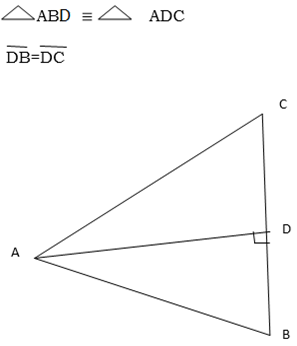
Solution

A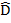 C= A
C= A B -right angles
B -right angles
Therefore
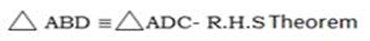
Note:
R.H.S – Right angle hypotenuse side
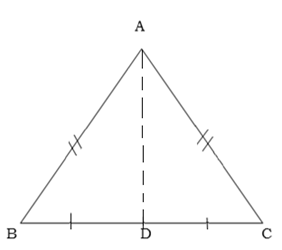
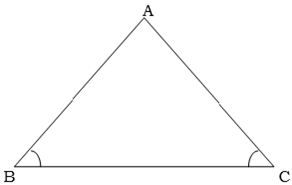
Isosceles triangle theorem
The base angles of an isosceles triangle are equal
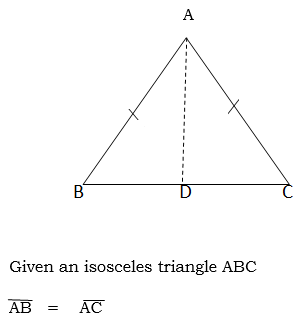

Construction:-

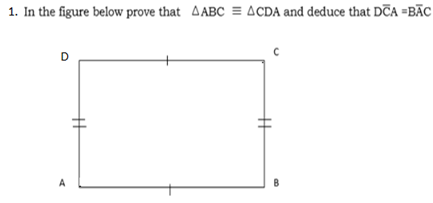
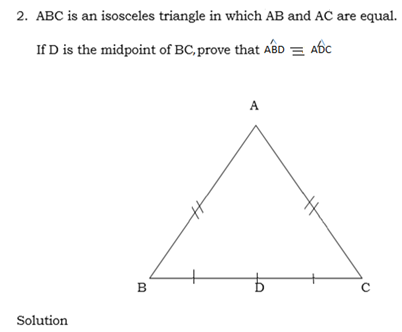
Exercise 1.

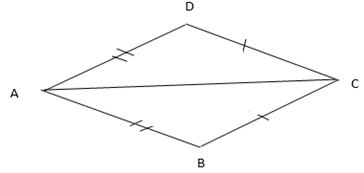

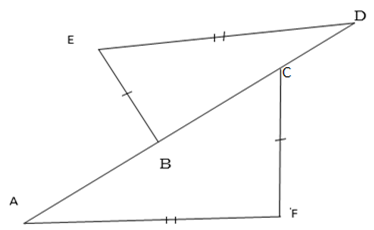
Solution
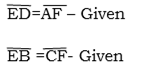
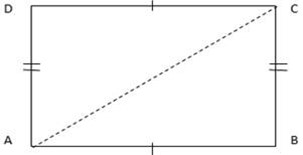
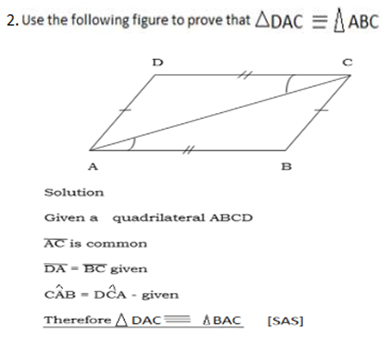
ABCD = Common line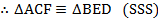

They are alternate interior angle

AB=CD given
BC =AD given

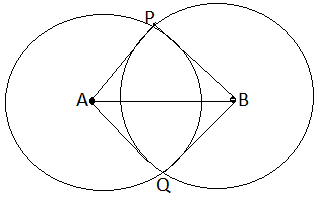
SOLUTION


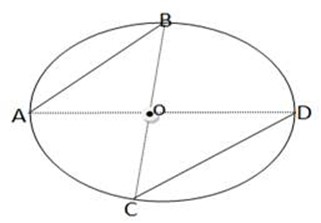
6. O is the center of the circle ABCD, if AC and BD and diameter of the circle and the line segments AD, AB and CB are drawn prove that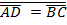
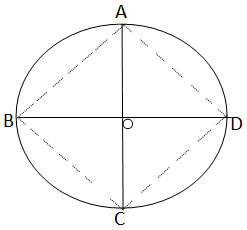
Solution

CONVERSE THE ISOSCELES TRIANGLE THEOREM
If two angles of a triangle are equal then sides opposite those angles are equal
Given that 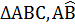 C=
C=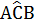
Required to prove 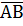 =
= 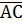
Construction A and D are joined such that

THEOREMS OF PARALLELOGRAMS
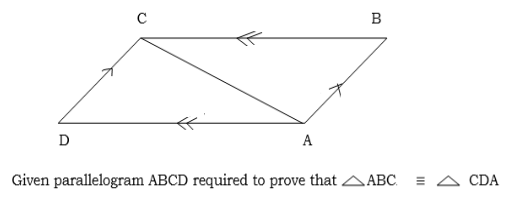
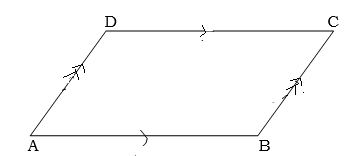
1) The opposite sides of the parallelogram are equal
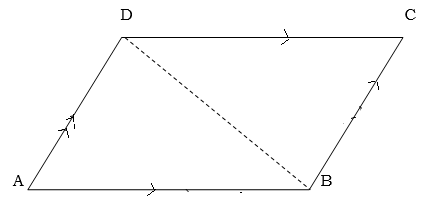
Given a parallelogram ABCD
Required to prove
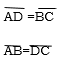
Construction:D is formed to B
A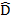 B= C
B= C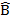 D -is interior angles AB//DC
D -is interior angles AB//DC
A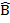 D= B
D= B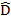 C -is interior angles AB//DC
C -is interior angles AB//DC
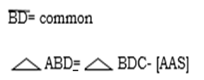
Therefore

2. The opposite angles of the parallelogram are equal
D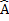 B= D
B= D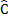 B
B
A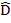 C + D
C + D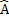 B=180
B=180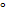 Interior angle of the same side of
Interior angle of the same side of 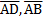 //
// 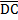
A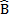 C + D
C + D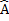 B=180º interior angles on side of
B=180º interior angles on side of 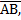
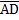 //
//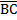
Therefore
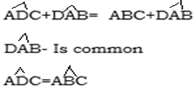
Similarly
D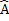 B + A
B + A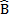 C=180º interior angles the same side of
C=180º interior angles the same side of 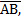
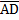 //
//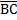
B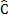 D + A
D + A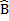 C=180º interior angles the same side of
C=180º interior angles the same side of 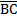 ,
,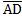 //
// 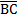
Therefore
D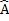 B + ABC= B
B + ABC= B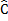 D + A
D + A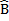 C
C
D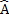 B= B
B= B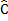 D
D
Hence opposite angles of a parallelogram are equal.
3.The diagonals of a parallelogram bisect each other
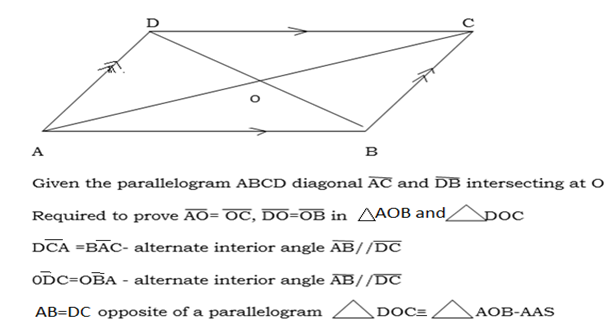
4. The diagonals of a parallelogram intersect each other
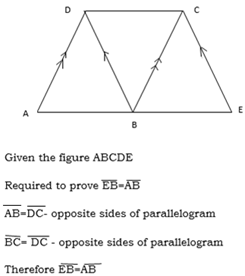
If one pair of the opposite sides of a quadrilateral are equal and parallel then the other pair of the opposite side are equal and parallel.
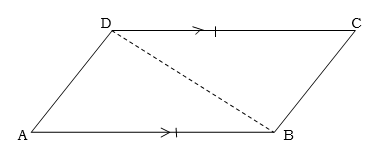

Example