EXPONENTS:
– Is the repeated product of real number by itself
e.g. i) 2 x 2 x 2 x 2 = 24
ii) 6 x 6 x 6 x 6 x 6 = 65
iii) a x a x a x a x a = a5
LAWS OF EXPONENTS
MULTIPLICATION RULE
Suppose;
4 x 4 x 4 = 43
Then, 43 = power
4 = base
3 = exponent
Suppose, 32 x 34 = 3(2+4) = 36
32 x 34 = 3 x 3 x 3 x 3 x 3 x 3 = 36

Example 1
Simplify the following
i) 64 x 68 x 66 x 61
ii) y4 x y0 x y3
Solution:
i) 64 x 68 x 66 x 61 = 6 4+8+6+1
= 619
ii) y4 x y0 x y3
Solution:
Y4 x y0 x y3 = y4+0+3
= y7
Example 2
Simplify the following
i) 32 x 54 x 33 x 52
ii) a3 x b3 x b4 x a5 x b2
Solution:
i) 32 x 54 x 33 x 52 = 32+3 x 54+2
= 35 x 56
ii) a3 x b3 x b4 x a5 x b2 = a3+5 x b3
= a8 x b9
Example 3
If 2Y x 16 x 8Y = 256, find y
Solution:
2y x 24 x 8y = 256
2y x 24 x 8y = 28
2y x 24 x (23)y = 28
y + 4 + 3y = 8
y + 3y = 8 – 4
4y = 4
Y = 1
Exercise 1:
1. Simplify
i) 34 x 43 x 38 x 34 x 42 = 34+8+4 x 43+2 = 316 x 45
ii) a2 x a3 x a4 x b2 x b3 = a2+3+4 x b2+3 = a9 x b5
2. If 125m x 252 = 510 find m
Solution:
125m x 252 = 510
53m x 54 = 510
3m + 4 = 10
3m = 10 – 4
3m=6
m = 2
3. If x7 = 2187. Find x
Solution:
X7 = 2187
X7 = 37
X = 3
QUOTIENT LAW
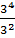 =
= 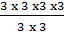 = 3 X 3
= 3 X 3
= 32
Also  = 34-2 = 32
= 34-2 = 32
Generally:

Example 1.
Find i) 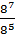 = 87-5
= 87-5
= 82
ii) 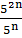 = 52n-n
= 52n-n
= 5n
Example 2.
If 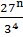 = 81 find n
= 81 find n
Solution:
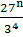 = 81
= 81
( ) = 34
) = 34
33n – 4 = 34
Equate the exponents
3n – 4 = 4
n= 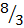
NEGATIVE EXPONENTS
Suppose  = 32 – 4 = 3-2
= 32 – 4 = 3-2
Also  =
= 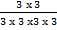
= 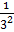

and Inversely xn = 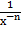
Example
Find
( i) 2-3 = 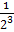 =
= 
(ii) 9-1/2 = 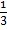
(iii) 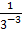 = 33 = 27
= 33 = 27
EXERCISE 2
1. Given 23n x 16 x 8n = 4096 find n
2. Given 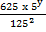 = 56 find y
= 56 find y
3. If 32n+1 – 5 = 76 find n
4. Given 2y = 0.0625.Find y

6. Find the value of x
(i). 81-1/2 = x
ii) 2-x = 8
ZERO EXPONENTS
Suppose,
 =
=  = 1
= 1
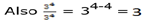
30 = 1
Example
Show that 90 = 1
Consider 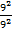 =
= 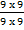 =
= 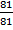 = 1
= 1
Also 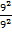 = 92-2 = 90
= 92-2 = 90
90 = 1 hence shown
Also
(i) 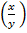 m =
m = 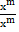
(ii) (x 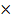 y)m = xm
y)m = xm
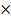 ym
ym
Example
(1)Find
i) (5 x 4)2
Solution:
(5 x 4)2 = 52 x 42
5 x 5 x 4 x 4 = 400
ii) ( )3
)3
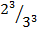 =
= 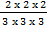 =
= 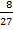
2. Show that 2-1 = 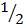
Solution:
2-1 = 
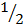 =
= 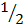
consider LHS
2-1 = 
L H S = R H S
Therefore
2-1 = 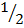 hence shown
hence shown
FRACTIONAL EXPONENTS AND EXPONENTS OF POWERS
EXPONENTS OF POWERS
Consider (54)3=(5x5x5x5)3
=(5x5x5x5)x(5x5x5x5)x(5x5x5x5)
=5x5x5x5x5x5x5x5x5x5x5x5
=512
Similarly (54)3=54×3
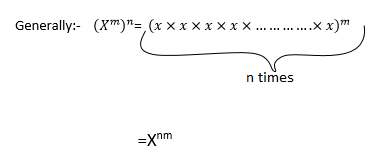

Examples:
1.Simplify (a (x4)5
(b) (86)3
Solution
(a) (x4)5=x4×5
=x20
(b) (86)3= 86×3
=818
2.Write 23x 42 as a power of single number
Solution
23x 42 ,but 4=22
therefore 42=(22)2
42=22×2
=24
23x 24=23+4
∴23x 24=27
FRACTIONAL EXPONENT
Solution
Consider the exponents of powers when  is squared, we get
is squared, we get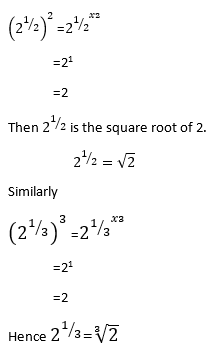
Let x be positive number and let n be a natural number. Then
Examples:
(1) Find 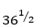
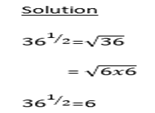
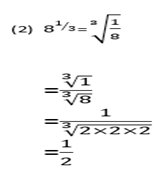
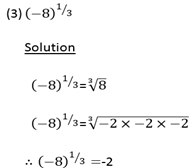
Thus if x is a negative number, and n is an odd number
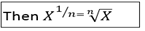
Exercise 2.
1. Show that 2-2 = 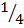
Solution:
Consider LHS
2-2 = 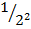 =
= 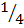
2-2 = 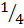
LHS = RHS hence shown
2. Evaluate
272/3 x 729 1/3 ÷ 243
Solution:
27 2/3 x 729 1/3 ÷ 243
(33)2/3 x (36)1/3 ÷ 35
32 x 32 ÷ 35
32+2-5
= 3-1 or 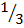
3. Find the value of m
(1/9)2m x (1/3)-m ÷ (1/27)2 = (1/3)-3m
Solution:
(1/32)2m x 1/3-m ÷ (1/33)2 = 1/3-3m
(1/3)4m x (1/3)-m ÷ (1/3)6 = (1/3)3m
3-4m x 3-m ÷ 3-6 = 3-3m
-4m + -m – 6 = -3m
-5m – 6 = -3m
6 = -2m
m = -3
4. Given 2x x 3y = 5184 find x and y
Solution:
2x = 5184 2x x 3y = 26 x 3y
2x = 26 By comparison
2x = 26 2x = 26
X = 6
3y = 5184 3x = 34
3y = 34
y = 4
The value of x and y is 6 and 4 respectively
RADICALS
-A number involving roots is called a surd or radical.
-Radical is a symbol used to indicate the square root, cube root or nth root of a number.
-The symbol of a radical is 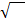
 Example of Radicals
Example of Radicals
(i) 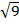
(ii) 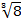
(iii)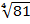
PRIME FACTORS
Example 1
Find (i) by prime factorization
by prime factorization
Solution:
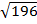 =
= 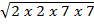
= 2×7
= 14
 ii)
ii) 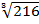 by prime factorization
by prime factorization
solution:
 =
= 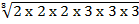
= 2 x 3
= 6
iii) 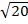 by prime factorization
by prime factorization
solution:
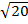 =
= 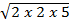
= 2 
Example 2
If 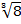 = 8x find x
= 8x find x
Solution:
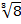 =
= 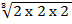 = 8x
= 8x
= (23)1/3 = 23x
= 21 = 23x
x= 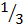

Exercise 3
1. Find the following
i) 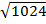
Solution
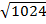 =
= 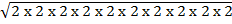
= 2 x 2 x 2 x 2 x 2
= 32
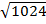 =32
=32
ii) 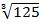
Solution
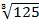 =
= 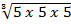
= 5
2. Simplify
a) 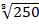 Solution
Solution
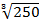 =
= 
= 5 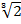
b) 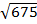 =
=
= 3 x 5 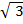
= 15 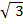
3. Find 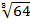 = 16y find y
= 16y find y
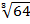 =
=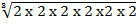 = 24y
= 24y
2 2 = 24y
2 = 4y
y = 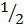
4. Find x if
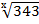 =491/3
=491/3
Solution
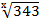 =
= 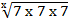 = 491/3
= 491/3
3431/x = 73/x = (72)1/3
73/x = 7 2/3
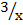 =
= 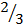
2x = 9
x =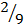
ii) 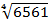 = 81x
= 81x
solution
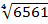 =
=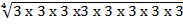 = 81x
= 81x
= 32 = 34x
= 2 = 4x
x = 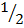
OPERATION ON RADICAL
ADDITION
Example1.
Evaluate
i) 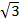 +3
+3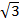
Solution: 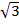 + 3
+ 3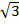 =(1 + 3)
=(1 + 3) 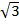
=4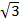
ii) 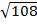 +
+ 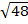
Solution
=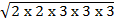 +
+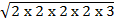
(22)1/2 (32)1/2
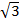 + (22)1/2 (22)1/2
+ (22)1/2 (22)1/2
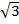
= (2 x 3) 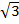 + (2 x 2)
+ (2 x 2) 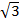
= 6 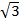 + 4
+ 4 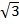
= 10 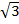

SUBTRACTION
Example
Evaluate
i) 3 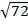 – 2
– 2 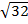
Solution
= 3 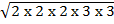 n-2
n-2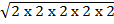
= (3 x 2 x 3 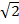
 2 x 2 x 2
2 x 2 x 2 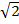 )
)
= 18 
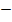 8
8 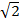
= 10 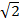
ii) 
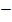
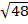
Solution
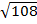
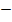
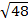 =
= 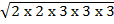
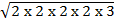
=(2 x 3) 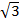
 (2 x 2)
(2 x 2) 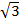
= 6 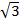
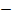 4
4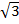
= 2 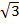
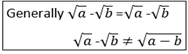
MULTIPLICATION
Example
Find i) 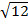 x
x 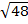
solution
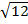 x
x  =
= 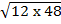
= 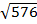
= 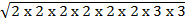
= 2 x 2 x 2 x 3
= 24
ii) 3 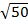 x 3
x 3
Solution
3 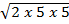 x 3
x 3 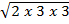
(5 x 3) 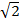 x (3 x 3)
x (3 x 3) 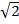
= 15 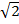 x 9
x 9 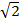
= 135 
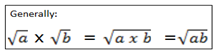
DIVISION
Example 1
Find i) 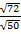
Solution: 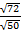 =
= 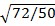
= 
= 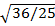
= 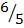

EXERCISE 4.
1. Find 2 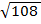 + 3
+ 3 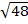
Solution: 2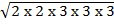 +3
+3 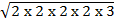
= (2 x 2 x 3)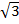 + (3 x 2 x 2)
+ (3 x 2 x 2)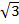
= 12 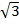 +12
+12 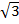
= 24 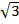
(ii )3 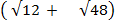
Solution:
3 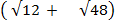 = 3
= 3 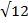 + 3
+ 3 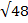
= 3 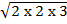 + 3
+ 3 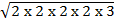
=(3 x 2) 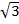 +(3 x 2 x 3)
+(3 x 2 x 3) 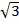
= 6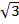 +12
+12 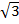
= 18 
(iii) 6 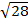
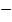 2
2 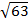
Solution:
6 
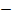 2
2  6 =
6 = 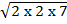
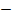 2
2 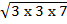
= (6 x 2) 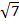
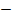 (2 x 3)
(2 x 3) 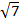
= 12 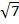
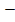 6
6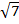
= 6 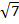
iv) 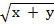 +
+ 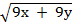
Solution:
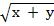 +
+ 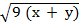
 +3
+3 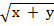
4 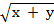
(v) 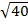 + 2250
+ 2250
Solution:
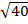 +
+ 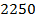 =
= 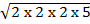 +2250
+2250
= 2 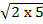 + 2250
+ 2250
=2 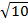 + 2250
+ 2250
=2 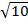 + 2250
+ 2250
2. Simplify
(i) 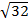 x
x 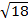
= 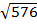
= 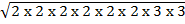
= 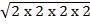
= 24
ii) 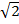
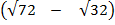
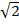 (
(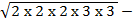
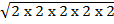 )
)
= 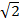 (2 x 3
(2 x 3 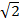 – 4
– 4 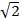 )
)
= 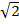 (6
(6 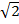 – 4
– 4 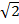 )
)
= 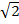 (2
(2 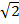 )
)
= 4
(iii) 3 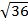 x 2
x 2 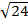
Solution:
= 3 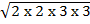 x 2
x 2 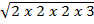
= 3 x 2 x 3 x (2 x 2) 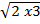
= 18 x 4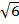
= 72 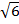
(iv) 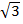 (15
(15 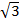 )
)
Solution:
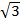 (15
(15 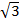 )= 15
)= 15 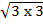
= 15 X 3
= 45
RATIONALIZATION OF THE DENOMINATOR
– Rationalizing the denominator involves the multiplication of the denominator by a suitable radical resulting in a rational denominator.
The best choice can follow the following rules:-
(i) If a radical is a single term(that is does not involve + or -),the proper choice is the radical itself,that is 
(ii)If the radical involves operations(+ or -),choose a radical with the same format but with one term with the opposite operation.
Examples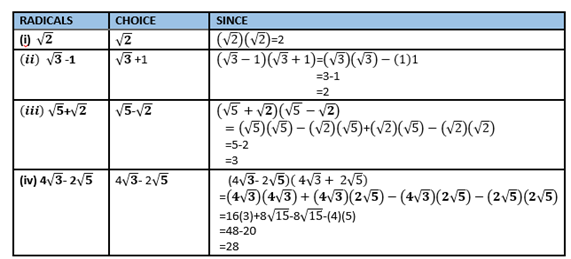
The same technique can be used to rationalize the denominator.
Example 1
Rationalize i) 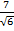
Solution 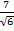 =
= 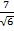 x
x 
= 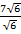
(ii) 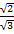
Solution:
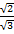 =
= 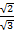 x
x 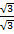
= 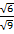
= 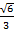
(iii) 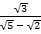
Solution:
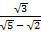 =
= 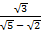 x
x 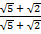
= 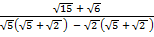
= 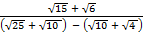
= 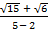
= 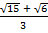
Example 2:
Rationalize (i) 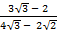
Solution:
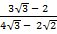 =
= 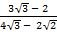 x
x 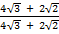
= 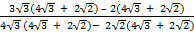
= 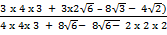
= 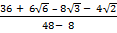
= 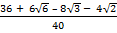
= 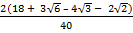
= 
(ii) Rationalize 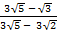
Solution:
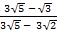 =
= 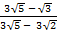 x
x 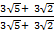
= 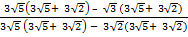
= 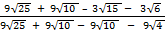
= 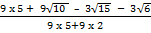
= 
= 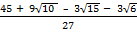
= 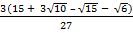
= 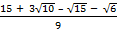
EXERCISE 5
1. Evaluate
(i) (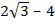 )(
)(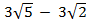 )
)
Solution:
(1) (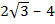 )(
)(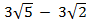 ) = (
) = (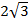 (
(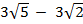 ) -4(
) -4(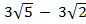 )
)
= 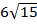 – 6
– 6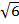 – 12
– 12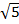 + 12
+ 12
(ii) ( )(
)(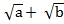 )
)
Solution:
(iii) (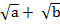 )(
)(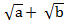 ) =
) = 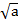 (
(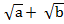 ) +
) + 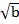 (
(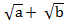 )
)
= a + 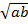 +
+ 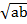 + b
+ b
= a + b + 2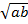
(iv) (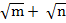 )(
)(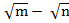 )
)
Solution:
(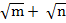 )(
)(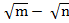 ) =
) = 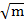 (
(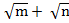 ) +
) + 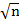 (
(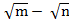 )
)
= m + 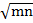 –
– 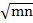 – n
– n
= m – n
(v) (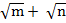 )(
)(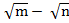 )
)
Solution:
( )(
)(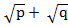 ) =
) = 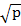 (
(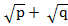 –
– 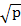 (
(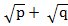 )
)
= p – 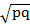 +
+ 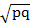 – q
– q
= p – q
2. Rationalize
(i) 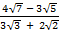
Solution:
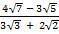 =
= 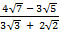 x
x 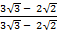
= 
= 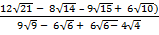
= 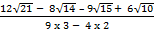
= 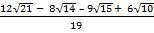
= 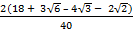
(ii) 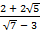
Solution:
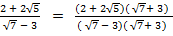
= 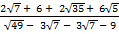
= 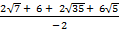
= – ( 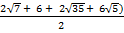 )
)
EXERCISE 6
Rationalize the following denominator
(i)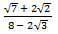
Solution:
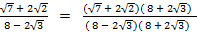
= 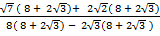
= 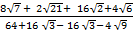
= 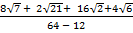
= 
(ii)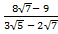
Solution:

= 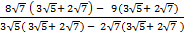
= 
= 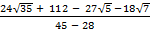
= 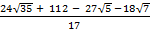
(iii) 
Solution:
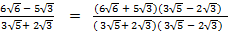
= 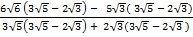
= 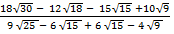
= 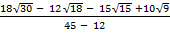
= 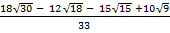
(iv) 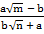
Solution:
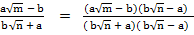
= 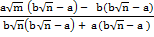
= 
= 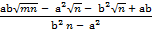
SQUARE ROOT OF A NUMBER
Example
Find( i) 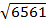
Solution
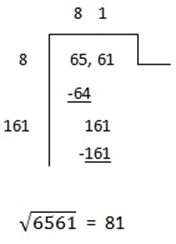
ii) 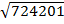
Solution:
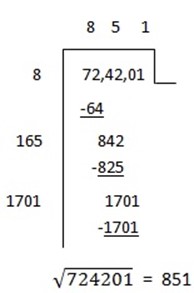
(iii)
Solution:

TRANSPOSITION OF FORMULA
A formula expresses a rule which can be used to calculate one quantity where others are given,when one of the given quantity is expressed in terms of the other quantity the process is called transposition of formula.
Example 1
The following are examples of a formula
a. A = 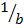
b. v = 
c. I = 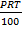
d. A =  (a +b)h
(a +b)h
e. T = 2 r
r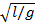
Example 2
The simple interest (I) on the principal (p) for time (T) years. Calculated at the rate of R% per annual is given by formula
I = 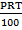
Make T the subject of a formula
Solution:
100 x I =  x 100
x 100
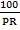 =
= 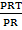
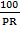 =
= 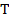
T = 
Example 3.
Given that
Y = mx + c, make m the subject
Solution:
Y = mx +c
 =
= 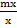
m = 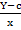
Example 4
Given that p = w 
Make a the subject.
Solution:
P = w 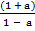
Divide by w both sides
 =
= 
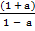
 =
= 
Multiply by (1 – a) both sides
 (1 – a) = (1
(1 – a) = (1 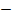 a)
a)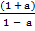
 (1 – a) = 1 + a
(1 – a) = 1 + a
 –
–  = 1 + a
= 1 + a
 – 1 = a +
– 1 = a + 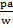
 – 1 = a(1 +
– 1 = a(1 +  )
)
Divide by 1 +  both sides
both sides
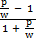 =
= 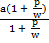
a = 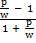
Alternatively
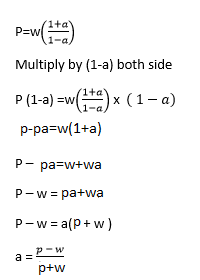
Example 5
Given that T = 2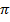
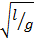 write g in terms of other letters
write g in terms of other letters
Solution:
T = 2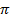
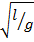
Divide by 2 both side
both side
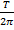 =
= 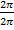

Remove the radical by squares both sides
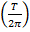 2 =
2 = 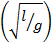 2
2
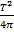 =
= 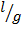
Multiply by g both sides
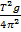 =
=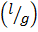 g
g
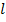 =
= 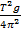
Multiply by 4 2 both sides
2 both sides
4 2 x
2 x 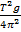 =
= 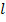 x 4
x 4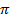 2
2
T2g = 4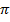 2
2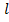
Divide by T2 both sides
∴ g = 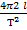
Example 6
If A = p + 
(i) Make R as the subject formula
(ii) Make P as the subject formula
Solution:
(i) A = p + 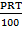
= A – P = 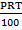
Multiply by 100 both sides
= 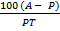 = R
= R
R = 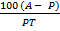
(ii) A = P + 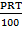
Solution:
Multiply by 100 both sides
100A = 100P + PRT
100A = P(100 + RT)
Divide by 100 + RT both sides
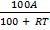 = P
= P
P = 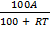
Exercise 7
1. If S = 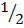 at2. Make t the subject of the formula
at2. Make t the subject of the formula
2. If c = 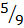 (F – 32) make F the subject of the formula
(F – 32) make F the subject of the formula
Solution:
S = 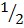 at2
at2
Multiply by 2 both sides
s x 2 = 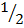 at2 x 2
at2 x 2
2s = at2
Divide by a both sides
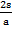 =
= 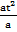
t2 = 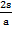
Square root both sides
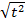 =
= 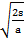
t = 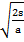
2. C = 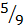 (F – 32)
(F – 32)
C = 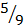 F –
F – 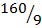
C + 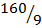 =
= 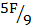
Multiply by 9 both sides
9C + 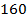 =
= 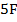
Divide by 5 both sides
F = 
More Examples
1. If A =  (a + b)
(a + b)
(i) Make h the subject formula
(ii) Make b the subject formula
2. If 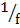 =
= 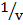 –
– 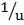
(i) Make f the subject formula
(ii) Make u the subject formula
Solution:
1. A = 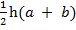
2A = 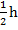 (a + b)x 2
(a + b)x 2
2A = 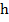 (a + b)
(a + b)
Divide by a + b both sides
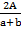 =
= 
h = 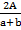
(ii) Make b the subject formula.
Solution:
A = 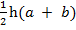
2A = 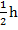 (a + b)x 2
(a + b)x 2
2A = 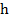 (a + b)
(a + b)
2A = ah + bh
2A 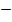 ah = bh
ah = bh
Divide by h both sides
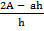 = b
= b
b = 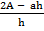
2. 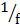 =
= 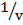 –
– 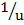
Solution:
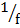 =
= 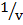 –
– 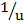
 =
= 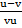
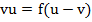
Divide by u – v both sides
f = 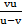
ii) Make u the subject formula
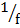 =
= 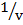 –
– 
Solution:
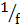 =
= 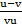
Multiply by uv both sides
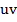 = f(u – v)
= f(u – v)
uv = fu – fv
fv = fu – uv
fv =u (f – v)
Divide by f – v both sides
u = 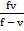
Exercise 8
1. If T = 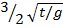
(i) Make t the subject formula
(ii) Make g the subject
2. If P = w 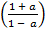
(i) Make w as the subject formula
(ii) Make a the subject formula
Solution:
1. (i)T = 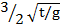
Square both sides
T2 = 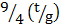
Multiply by 4 both sides
4T2 = 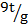
4T2g = 9t
Divide by 9 both sides
t = 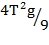
(ii) Make g the subject formula
T = 
Solution:
Square both sides
T2 = 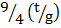
Multiply by 4 both sides
4T2 = 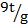
4T2g = 9t
Divide by 4T2 both sides
g = 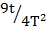
2)( i) Make w was the subject
Make a the subject
Solution:
P = w 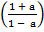
P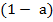 = w(
= w(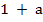 )
)
Divide by ( ) both sides
) both sides
w =P 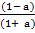
ii) Make a the subject formula
Solution:
P = w 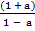
Divide by w both sides
 =
= 
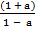
 =
= 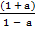
Multiply by (1 – a) both sides
 (1 – a) = (1
(1 – a) = (1 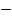 a)
a)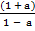
 (1 – a) = 1 + a
(1 – a) = 1 + a
 –
– 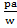 = 1 + a
= 1 + a
 – 1 = a +
– 1 = a + 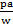
 – 1 = a(1 +
– 1 = a(1 +  )
)
Divide by 1 +  both sides
both sides
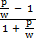 =
= 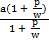
a = 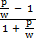
Exercise 9
I. If v = 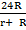 Make R the subject formula
Make R the subject formula
Solution:
v = 
Multiply by r + R both sides
v (r + R) = 24R
vr + Rv = 24 R
vr = 24R – Rv
vr = R (24 – v)
Divide by 24 – v both sides
2. If m = n 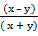
(i) Make x the subject formula
Solution:
m = n 
Multiply by x + y both sides
mx + my = nx – ny
my + ny = nx – mx
my + ny = x(n – m)
divide by n – m both sides
x = 
(ii)If T = 2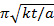
Make t the subject formula
Solution:
T = 2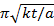
Square both sides
T2 = 4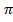 2
2
Multiply by a both sides
T2a = 4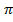 2kt
2kt
Divide by 4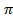 2k both sides
2k both sides
t =  2
2

ALGEBRA
– BINARY OPERATIONS
This is the operation in which the two numbers are combined according to the instruction
The instruction may be explained in words or by symbols e.g. x, *,
– Bi means two
Example1.
Evaluate
(i) 5 x 123
Solution:
5 x 123 = 5(100 + 20 + 3)
= 500 + 100 + 15
= 615
(ii) (8 x 89) – (8 x 79)
= 8(89 – 79)
= 8(10)
= 80
Example2
If a * b = 4a – 2b
Find 3 * 4
Solution:
a * b = 4a – 2b
3 * 4 = 4(3) – 2(4)
= 12 – 8
3 * 4 = 4
Example 3
If p * q = 5q – p
Find 6 * (3 * 2)
Solution:
– consider 3 * 2
From p * q = 5q – p
3 * 2 = 5q – p
= 10 – 3
= 7
Then, 6 * 7 = 5q – p
6 * 7 = 5(7) – p
35 – 6 = 29
6 *(3 * 2) = 29
35 – 6 = 29
6 * (3 * 2) = 29
BRACKETS IN COMPUTATION
– In expression where there are a mixture of operations, the order of performing the operation is BODMAS
(ii) B = BRACKET
O = OPEN
D = DIVISION
M = MULTIPLICATION
A = ADDITION
S = SUBTRACTION
Example
Simplify the following expression
(i) 10x – 4(2y + 3y)
Solution
10x – 4(2y + 3y)
= 10x – 4(5y)
= 10x – 20y
IDENTITY
– Is the equation which are true for all values of the variable
Example
Determine which of the following are identity.,
(i) 3y + 1 = 2(y + 1)
Solution:
3y + 1 = 2(y + 1)
Test y = 3
3(3) + 1 = 3(2 + 1)
9 + 1 = 3(3)
10 = 9
Now, LHS ≠ RHS (The equation is not an identity)
(ii) 2(p – 1) + 3 = 2p + 1
Test p = 4
2(4 – 1) + 3 = 2(4) + 1
2(3) + 3 = 8 + 1
6 + 3 = 9
9 = 9
Now, LHS  RHS (The equation is an identity)
RHS (The equation is an identity)
EXERCISE
1. If a * b = 3a3 + 2b
Find (2* 3) * (3 * 2)
Solution:
a* b = 3a3 + 2b
(2 * 3) = 3(2)3 + 2 x 3
= 3(8) + 6
= 24 + 6 = 30
Then
(3 * 2) = 3(3)3 + 2(2)
a * b = 30 * 85
30 * 85 = 3(30)3 + 2(85)
= 3(27000) + 170
= 81000 + 170
(2 * 3) * (3 * 2) = 81170
2. If x * y = 3x + 6y, find 2*(3 * 4)
Solution:
Consider (3 * 4)
From x * y = 3x + 6y
3 * 4 = 3(3) + 6(4)
= 9 + 24
= 33
Then 2 * 33 = 3x + 6y
2 *33 = 3(2) + 6(33)
= 6 + 198 = 204
2 * (3 * 4) = 204
3. If m*n = 4m2 – n
Find y if 3 * y = 34
Solution:
= m * n = 4m2 – n
= 3 * y = 34
= 3 * y = 4(3)2 – y = 34
= 4(32) – y = 34
= 4(9) – y = 34
36 – y = 34
y = 2
4. Determine which of the following is identities
2y + 1 = 2(y + 1)
Solution:
2y + 1 = 2(y + 1)
Test y = 7
2(7) + 1 = 2(7 + 1)
14 + 1 = 2(8)
15 = 16
Now, LHS  RHS (The equation is not an identity).
RHS (The equation is not an identity).
QUADRATIC EXPRESSION
Is an expression of the form of ax2 + bx + c.
– Is an expression whose highest power is 2.
– General form of quadratic expression is ax2 + bx + c where a, b, and c are real numbers and a ≠ 0.
Note
(i) a≠ o
bx – middle term
y = mx2 + cx – linear equation
y = ax + b
y= mx2 + 2 – quadratic equation
y = mx2 + c
example
(i) 2x2 + 3x + 6 (a =2, b =3, c =6)
ii) 3x2 – x (a =3, b = -1, c = 0)
iii) 1/2x2 – 1/yx – 5 (a = ½, b = -1/4, c = -5)
iv) –x2 – x – 1 (a = -1, b = -1, c = -1)
v) x2 – 4 (a = 1, b = 0, c = -4)
vi) x2 (a = 1, b = 0, c = 0)
Example
If a rectangle has length 2x + x and width x – 5 find its area
Solution:
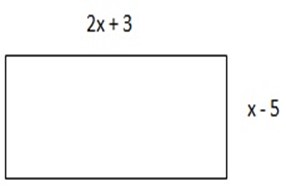
From, A = l x w where A is area, l is length and w is width
= (2x + 3) (x – 5) Alternative way:
= 2x(x – 5) + 3(x – 5) (2x + 3) X (x-5)
= 2x2 – 10x + 3x – 15 2x2 -10N + 3x-15
2x2 – 7x – 15unit area 2x2 – 7x-15 Unit area
EXPANSION
Example 1
Expand i) (x + 2) (x + 1)
Solution:
(x + 2) (x + 1) Alternative way:
x(x + 1) + 2(x + 1) (x+2) (x+1)
= x2 + x + 2x + 2 x2 +x+2x+2
= x2 + 3x + 2 x2+3x+2
ii) (x – 3) (x + 4) Alternative way:
x (x + 4) – 3(x + 4) (x-3) (x+4)
x2 + 4x – 3x – 12 x2+4x-3x-12
= x2 + x – 12 x2+x-12
iii) (3x + 5) (x – 4) Alternative way:
3x(x -4) + 5 (x – 4) (3x+5) (x-4)
= 3x2 – 12x + 5x – 20 3x2-12x+5x-20
= 3x2 – 7 – 20 3x2-7x-20
iv) (2x + 5) (2x – 5) Alternative way:
2x (2x – 5) + 5(2x – 5) (2x+5) (2x-5)
4x2 – 10x + 10x – 25 4x2-10x+10x-25
= 4x2 – 25 4x2-25
EXERCISE
I. Expand the following
(x + 3) (x + 3) Alternative way:
x(x + 3) + 3x + 9 (x+3) (x+3)
= x2 + 3x + 3x + 9 x2+3x +3x+9
= x2 + 6x + 9 x2+6x+9
iii) (2x – 1) (2x – 1)
Solution:
2x(2x – 1) – 1 (2x – 1)
=(2x-1) ( 2x-1)
= 4x2 – 2x – 2x + 1
= 4x2 – 4x +1
iii) (3x – 2) (x +2)
Solution:
3x(x + 2) – 2(x + 2) Alternative way:
= 3×2 + 6x – 2x – 4 (3x-2) (x+2)
= 3x2 + 4x – 4 3x2+6x-2x-4
3x2+4x-4
2) Expand the following
i) (a + b) (a + b)
Solution:
a(a + b) + b(a + b)
=(a+b) (a+b)
= a2 + ab + ba + b2
= a2 + 2ab + b2
ii) (a + b) (a –b)
Solution:
a(a + b) – b(a + b)
= (a+b) (a-b)
= a2 – ab + ab -b2
= a2 – b2
iii) (p + q) (p – q)
Solution:
p(p – q) + q(p – q) Alternative way:
= p2 – pq + qp – q2 (p+q) (p-q)
= p2 – q2 p2-pq+pq- q2
p2 – q2
iv) (m – n) (m + n)
Solution:
m(m + n) – n(m + n) Alternative way:
= m2 +mn – nm + n2 (m-n) (m+n)
= m2 – n2 m2 + mn -nm – n2
m2 – n2
v) (x – y) (x – y)
Solution:
x(x – y) – y(x – y)
= (x-y) (x-y)
= x2 – xy – yx + y2
= x2 – 2xy + y2
FACTORIZATION
– Is the process of writing an expression as a product of its factors
(i) BY SPLITTING THE MIDDLE TERM
– In quadratic form
ax2 + bx + c
Sum = b
Product =ac
Example i) x2 + 6x + 8
Solution:
Find the number such that
i) Sum = 6; coefficient of x
ii) Product = 1 x 8; Product of coefficient of x2 and constant term
= 8 = 1 x 8
= 2 x 4
Now
x2 + 2x + 4x + 8
(x2 + 2x) + (4x + 8)
x (x + 2) + 4(x + 2)
= (x + 4) + (x + 2)
ii) 2x2 + 7x + 6
Solution:
Sum = 7
Product, = 2 x 6 = 12
– 12 = 1 x 12
= 2 x 6
= 3 x 4
Now,
2x2 + 3x + 4x + 6
(2x2 + 3x) + (4x + 6)
= x (2x + 3) + 2(2x + 3)
= (x + 2) (2x + 3x)
iii) 3x2 – 10x + 3
Solution:
Sum = -10
Product = 3 x 3 = 9
9 = 1 x 9
= 3 x 3
Now,
3x2 – x – 9x + 3
(3x2 – x) – (9x + 3)
x(3x – 1) – 3(3x + 1)
(x – 3) (3x – 1)
iv) x2 + 3x – 10
Solution:
Sum = 3
Product = 1 x -10 = -10
= -2 x 5
Now,
X2 – 2x + 5x – 10
(x2 – 2x) + (5x – 10)
x (x – 2) + 5(x – 2)
= (x + 5) (x – 2)
EXERCISE
i) Factorize the following
4x2 + 20x + 25
Solution:
Sum = 20
Product = 4 x 25 = 100
100 = 1 x 100
= 2 x 50
= 4 x 25
= 5 x 20
= 10 x 10
= 4x2 + 10x + 10x + 25
(4x2 + 10x) + (10x + 25)
2x(2x + 5) + 5 (2x + 5)
= (2x + 5) (2x + 5)
ii) 2x2 + 5x – 3
Solution:
Sum = 5
Product = -6
number = (- 1,6)
= 2x2 – x + 6x – 3
= 2x2 + 5x – 3
(2x2 – x) + (6x – 3)
x (2x – 1) + 3(2x – 1)
= (x + 3) (2x – 1)
iii) x2 – 11x + 24
Solution:
Sum = -11
Product = 1 x 24 = 24
24 = 1 x 24
= 1 x 24
= 2 x 12
= 3 x 8 = -3 x -8
= 4 x 6
x2 – 3x – 8x + 24
(x2 – 3x) – (8x – 24)
x(x – 3) – 8(x – 3)
= (x – 8) (x – 3)
iv) x2 – 3x – 28
Solution:
Sum = -3
Product = 1 x -28 = -28
28 = 1 x 28
= 2 x 14
= 4 x 7
7
= x2 + 4x – 7x – 28
(x2 + 4x) – (7 + 28)
x(x +4) – 7(x +4)
(x – 7) (x + 4)
BY INSPECTION
Example
Factorize
i) x2 + 7x + 10
Solution:
(x + 2) (x + 5)
ii) x2 + 3x – 40
Solution:
(x – 5) (x + 8)
iii) x2 + 6x + 7
Solution:
Has no factor.
DIFFERENT OF TWO SQUARE
 Consider a square with length ”a” unit
Consider a square with length ”a” unit
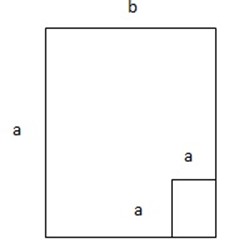
1st case, At = (a x a) – (b x b)
= a2 – b2
2nd case
A1 = a (a – b) …….(i)
A2 = b (a – b)…….(ii)
Now, 1st case = 2nd case
AT = A1 + A2
a2 – b2 = a (a – b) + b(a – b)
= (a + b) (a – b)
Generally a2 – b2 = (a + b) (a – b)
Example 1
Factorize i) x2 – 9
ii) 4x2 – 25
iii) 2x2 – 3
Solution:
i) x2 – 9 = x2 – 32
= (x + 3) (x – 3)
ii) 4x2 – 25 = 22x2 – 52
= (2x)2 – 52
iii)2x2 – 3 =(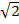 )2 x2 – (
)2 x2 – ( 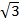 )2
)2
= (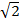 x)2 – (
x)2 – (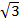 )2
)2
=(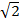 x +
x + 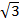 ) (
) (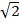 x –
x – 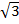 )
)
EXERCISE
I. Factorize by inspection
i) x2 + 11x – 26
Solution:
(x + 13) (x -2)
ii) x2 – 3x – 28
Solution:
(x – 7) (x + 4)
2. Factorization by difference of two square
i) x2 – 1
Solution:
X2 – 1 = (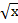 )2 – (
)2 – (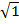 )2
)2
= (x)2 – 1
= (x + 1) (x – 1)
ii) 64 – x2
Solution:
64 – x2 = 82 – x2
= (8 + x) (8 – x)
iii) (x + 1)2 – 169
solution:
(x + 1)2 – 169
(x + 1)2 – 132
= (x + 1 – 13) (x + 1 + 13)
= (x – 12) (x + 14)
iv) 3x2 – 5
Solution:
3x2 – 5 = (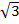 x)2 – (
x)2 – (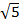 )2
)2
= (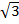 x –
x – 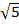 ) (
) (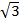 x +
x + 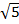 )
)
APPLICATION OF DIFFERENCES OF TWO SQUARE
Example 1
Find the value of i) 7552 – 2452
ii) 50012 – 49992
Solution:
i) 7552 – 7452
From a2 – b2 = (a + b) (a – b)
7552 – 2452 = (755 – 245)(755 + 245)
= (510) (1000)
= 510, 000
ii) 50012 – 49992
50012 – 49992 = (5001 – 4999) (5001 + 4999)
50012 – 49992 = (5001 + 4999)
= (2) (10000)
= 20,000
PERFECT SQUARE
Note
(a + b)2 = (a + b) (a + b)
(a – b)2 = (a – b) (a – b)
Example
Factorize i) x2 + 6x + 9
Sum = 6
Product = 9 x 1 = 9
= 9 = 1 x9
= 3 x 3
x2 + 3x + 3x + 9
(x2 + 3x) + (3x + 9)
= x (x + 3)+3 (x + 3)
= (x + 3)2
ii) 2x2 + 8x + 8
Sum = 8
Product = 2 x 8 = 16
16 = 1 x 16
= 2 x 8
= 4 x4
2x2 + 4x + 4x + 8
(2x2 + 4x)+ (4x + 8)
2x(x + 2) +4(x + 2)
(x +2) (2x + 4)
For a perfect square ax2 + bx + c
Then 4ac = b2
Example 1
If ax2 + 8x + 4 is a perfect square find the value of a
Solution:
ax2 + 8x + 4
a = a, b = 8, c = 4
From,
4ac = b2
4(a) (4) = 82
16a/16 = 64/16
a = 4
Example2
If 2x2 + kx + 18 is a perfect square find k.
Solution:
2x2 + kx + 18
a = 2, b = kx, c = 18
from
4ac = b2
4(2)(18) = k2
From
4ac = b2
4(2) (18) = k2
 =
= 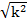
K = 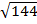
K = 12
– Other example
Factorize i) 2x2 – 12x
Solution:
2x(x – 6)
ii) x2 + 10x
= x(x + 10)