LOGARITHMS
STANDARD NOTATIONS
Standard notation form is written in form of A x 10n whereby 1≤ A< 10 and n is any integers
Example
Write the following in standard form
(i) 2380
Solution:
2380 = 2.38 x 103
(ii) 97
Solution:
97 = 9.7 x 101
(iii) 100000
Solution:
100000 = 1 x 105
(iv) 8
Solution:
8 = 8 x 100
Example
Write the following in standard form
(i) 0.00056
= 5.6 x 10-4
(ii) 0.001
= 1 x 10-3
(iii) 0.34
= 3.4 x 10 -1
(iv) 2. 0001
= 2. 0001 x 100
EXERCISE 1:
i). Write the following in standard form
17000
= 1.7 x 104
ii) 0.00998
= 9.98 x 10-3
iii). Write in standard form
0.000625
= 6.25 x 10-4
8/300 correct to four significant figure
8/300 = 0.02666
Now 2.667 x 10-2
2.667 x 10-2
iv) If a = br and a = 8.4 x 104 , b = 7.0 x 102 Find r.
solution:
a = 84 000
b = 700
Now
br = a
(700) (r) = 84000

r=120
r = 1.2 x 102
DEFINITION OF LOGARITHMS
Consider
3 x 3 x 3 x 3 then
3 x 3 x 3 x 3 = 34 = 81, the number 3 is the base ,and 4 is the exponent.
Now we say;
Logarithm of 81 to base 3 is equal to exponent 4
log381 = 4
In short bn = a
logba= n
Example 1.
Write the following in logarithmic form
i) a5 = 10
loga10 = 5
ii)10-3 = 0.001
10-3= 0.001
log100.001 = -3
iii) 2-1 = ½
log21⁄2 = -1
iv) 3 = 91/2
log39 = 1⁄2
Example 2
Write the following in exponential form
(i) log3729= 6
36 = 729
(ii) log31⁄3 = -1
3-1 = 1/3
(iii) log100.01 = -2
10-2 = 0.01
(iv)1⁄2 = log42
4(1/2) = 2
Example 3
If log100.01= y. Find y
Solution:
log100.01 = y
10y = 0.01
10y =1×10-2
10y=100×10-2
10y=10-2
y= -2
If log10x=-3 find x
Solution:
log10x = -3
10-3 = x
x=0.001
EXERCISE 1
1. Write in standard form
i) 405.06
ii) 0.912
Solution:
i) 405.06 = 4.0506 x 102
ii) 0.912 = 9.12 x 10-1
2. Write in logarithimic form
i)5-1 = 1⁄5
ii) 0.0001 =1 × 10-4
Solution:
i) 5-1 = 1⁄5
log5(1⁄5) = -1
ii) 0.0001 = 10-4
log100.0001 = -4
3. Write in exponential form
i) logax = n
ii)-3 = log100.001
iii) log2(1⁄64) = -6
Solution:
i) logax = n
an = x
ii)-3 =log100.001
10-3 = 0.001
iii) log2(1⁄64) = -6
2-6 = 1⁄64
4. To solve for x
i) log6x= 4
64 = x
x = 1296
ii) x = log36561
3x = 6561
x = 8
iii) logx10= 1
x1 = 10
x = 10
iv) log42 = x
4x = 2
22x = 21
2x= 1
x = 1⁄2
BASE TEN LOGARITHM
– Is an logarithm of a number to base 10. Also known as common logarithm
example i) log105= log5
ii) log1075 = log75
iii) log10p = log p
SPECIAL CASES
(1). logaa = x
ax = a1
x = 1

Generally logaa = 1
Example
i) log66 = 1
ii) log10 = 1
(2) loga(an) = x
ax = an
x = n
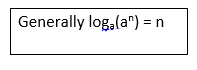
Example i) log4(45) = 5
ii) log10-3 = -3
Example 1
If log55 = log2m Find m
Solution:
log55 = log2m
But log55 = 1
1 = log2m
21 = m1
m = 2
Example 2
Given log525 + log4x = 6, Find x
Solution:
log525 + log4x = 6
log5(52)+ log4x = 6
2log55+log4x = 6
2 +log4x = 6
log4x = 4
x= 44
x = 256
EXERCISE 2.
Evaluate
i) log24096
ii) log0.0001
solution
i) log24096
let x = log24096
2x = 4096
2x = 212
x = 12
∴log24096=12
ii) log0.0001
Solution:
Let x = log0.0001
10x = 1/10000
10x = 1/(104)
10x = 10-4
x = -4
∴log0001=1
2) If logk81 – log232= -1
Solution:
logk81 – 5log22 = -1
logk81 = -1 + 5
logk81= 4
k4 = 81
k4 = 34
k = 3
3. Given log6y = log7343. Find y
Solution:
log6y = 3log77
log6y = 3
63 = y
216 = y
y = 216
4) Solve for m
i) log81 = m
8m = 1 since aº=1 then
8m=80
m=0
ii) log5m + log327 = 8
log5m + log333= 8
log5m +3 = 8
log5m = 5
m= 55
m = 3125
LAWS OF LOGARITHMS
MULTIPLICATION LAW
Suppose, logax = p and logay = q then
logax = p….(i)
logay = q….(ii)
Write equation (i) and (ii) into exponential form.
ap = x………(iii)
aq = y……..(iv)
Multiply equation (iii) and (iv)
xy = ap x aq
xy = a(p + q) …….(v)
In equation (v) apply loga both sides
loga (xy) = logaa(p + q)
logaxy = (p + q) logaa
logaxy = p + q
But p = logax
q = logay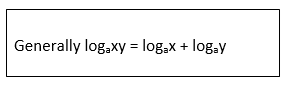
Example
i) log6(8 ×12) = log88 + log612
ii) log49 +log43 = log4(9 ×3)
Example 1
i) Find x , If log3x = log315 + log312
Solution:
log3x = log315 + log312
log3x = log3( 15 ×12)
log3x = log3180
∴ x = 180
Example 2
Given log520 = log54 + log5x .Find x
Solution:
log520 = log54 + log5x
log520 = log5(4 × x)
log520 = log54x
∴20 = 4x
X = 5
Example 3
If log80.01= log8(m ×2). Find m
solution
log80.01 = log8( 2m)
∴ 0.01 = 2m
m = 0.01/2
m = 0.005
QUOTIENT LAW
Suppose, logax= p and
logay = q then
logax = p……..(i)
logay = q……..(ii)
Write equation (i) and (ii) into exponent form
ap = x……(iii)
aq = y…..(iv)
Divide equation (iii) and (iv)
x/y = ap/aq
x/y = a(p – q) ….. (v)
In equation (v) apply log a both sides
loga(x/y) = logaa(p-q)
loga(x/y) = (p – q) logaa
But logaa = 1
loga(x/y) = p – q ,where p= logax and q=logay
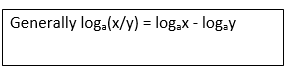
i) log6( 8/12) = log68 – log612
ii) log49 – log43 = log4(9/3)
Example
If log220 = log2x – log28.Find x
Solution:
log220 = log2x – log28
log220 = log2(x/8)
Now, 20 = x/8
X = 20 x 8
X = 160
EXERCISE 3
1. Evaluate
i) log63 + log62
Solution:
= log63 + log62
= log6( 2 ×3)= log66
= 1
ii) log 40 + log 5 + log40
Solution:
= log1040 + log105 + log1040
= log10( 40 ×5 ×40)
=log108000
iii) log1025 – log109 + log10360
Solution:
log1025 – log109 + log10360
log10( (25 ×360 )/9)
=log101000
=log10103
=3log1010
=3
2. If log5aâ¡x = log5aâ¡9 + log5aâ¡12. Find x
Solution:
log5aâ¡x = log5aâ¡9 + log5â¡a12
log5aâ¡x = log5aâ¡( 9 ×12)
log5aâ¡x = log5aâ¡108
x = 108
3. If log2aâ¡5 = log2ay + log2aâ¡0.001.Find Y
Solution:
i) log2aâ¡5 = log2aâ¡(y×0.001)
5â¡ = â¡0.001y
y= 5/0.001
Y = 5000
ii)Find y if log6â¡100 = log6â¡5 + log6â¡80 – log6â¡y
Solution:
log6â¡100 = log6 (5 × 80)/ y
100 = â¡400/y
y = 4
4. If log a = 0.9031, log b = 1.0792 and log c = 0.6990. Find logâ¡ ac⁄b
Solution
log â¡ac⁄b =log10â¡ a + log10â¡c – log10â¡b
=0.9031 + 1.0792 -0.6990
∴ log â¡ac⁄b = 1.2833
LOGARITHM OF POWER
If logaâ¡x = p then
X = ap
Multiply by power in both sides xn = anp
Apply log a both sides
logaxn = logaanp
logaxn = np
But p = logax
∴ logaxn= nlogax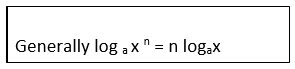
Example(1)
Evaluate
i) log2 (128)6
ii) log7 (343)8
Solution
i) log2 (128)6 = 6log2 27
= (7 x 6) log22
= 42 x 1
= 42
ii) Log7 (343)8
Solution:
log7 3438 = 8log7 343
= 8log7 73
= (8 x 3) log7 7
= 24
Example (2)
If log5 625y = log3 7292 .Find y.
Solution:
log5 625y = log3 7292
log5 625y = 2log3 729
ylog5 54 = 2log3 36
(y x 4) log5 5 = (2 x 6) log3 3
4y log5 5 = 12 log3 3
4y = 12
y=2/4
y = 3
LOGARITHM OF ROOTS
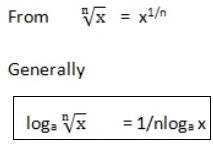
Example (1)
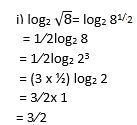
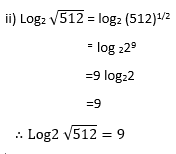
EXERCISE 4:
1. Evaluate
i) log 60 + log 40 – log 0.3
ii) log3 √(1⁄27)
Solution:
i) Log60 + log40 – log0.3
log10 60 + log10 40 – log10 0.3
log10 (60 x 40/0.3) = log10 (2400/0.3)
= log10 8000
=3.9031
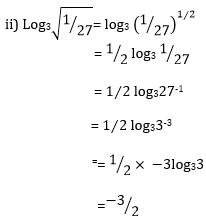

3. Given log2 x = 1 – log2 3. Find x
Solution:
log2 x = 1 – log2 3
log2 x = log2 2-log2 3
log2 x = log2 (2/3)
x =2/3
4. Simplify
i) 2log5 + log36 – log9
ii) (logâ¡8-logâ¡4)/(log 4-log2)
Solution:
i) 2log5 + log36 – log9
log52 + log36 – log9
log1025 + log1036 – log109
= log10 (25 x 36)/9
= log10 (900/9)
= log10100
=log10 102
=2 log10 10
=2
ii) (logâ¡8-logâ¡4)/(log 4-log2)
Solution:
(logâ¡8-logâ¡4)/(log 4-log2)
= log10 (8/4) ÷log10 (4/2)
= log102 ÷ log102
= 1