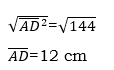PYTHAGORAS THEOREM
Pythagoras theorem is used to solve problems involving right angled triangles.
Statement:
In a right- angled triangle the square on the hypotenuse is equal to the sum of the squares on the other two sides.
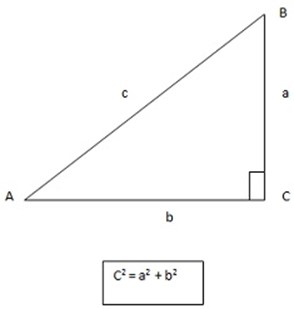
Shown below
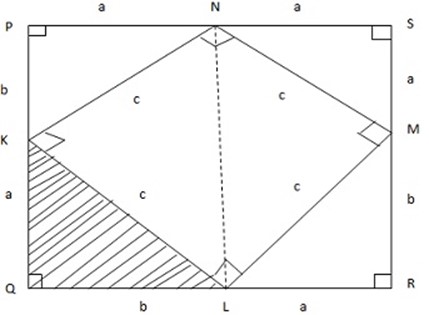
Required to prove: c2 = a2 + b2
Construction : Joining L and N. Considering the trapezium PQLN:
Area of the trapezium
but area of trapezium = area Δ PKN + area Δ KQL + area Δ KLN
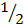 (a+b) (a+b) =
(a+b) (a+b) = 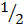 ab +
ab + 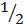 ( c x c)
( c x c)
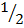 (a+b) (a+b) = ab +
(a+b) (a+b) = ab + 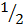 c2
c2
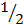 [a2 + 2ab + b2] = ab +
[a2 + 2ab + b2] = ab + 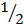 c2
c2
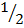 a2 + ab +
a2 + ab + 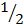 b2 = ab +
b2 = ab + 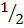 c2
c2
|
edu.uptymez.com |
edu.uptymez.com
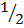 a2 +
a2 + 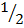 b2 =
b2 = 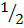 c2
c2
Pythagoras theorem
Examples
1.The side s of a triangle containing the right angle have length of 5cm and 12cm.
Find the length of the hypotenuse
Solution
C2= a2 +b2
C2 = 52 + 122
C2 = 25+ 144
C2 = 169
C = 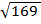
C= 13cm
∴ The length of the hypotenuse = 13cm.
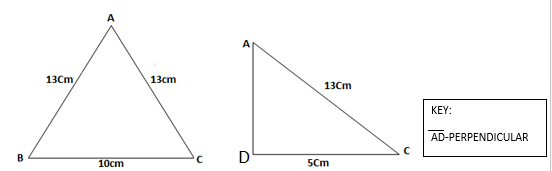
2. In figure below if AC =17cm, BC = 8cm, and CD = 12cm find AD
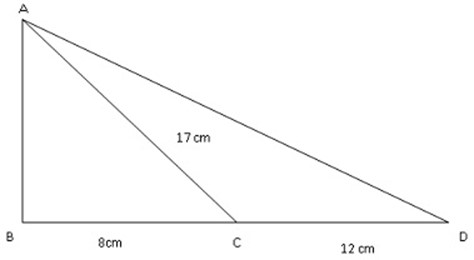
Solution: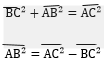
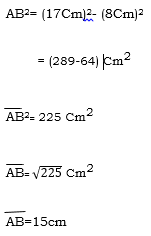
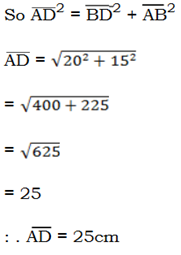
EXERCISE
1. Calculate the unknown side of the following triangle
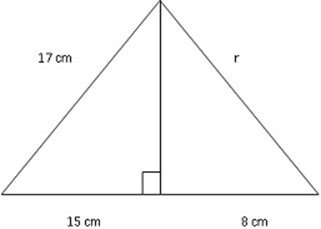
SOLUTION:
172 = 152 + b2
b2 = 172 – 152
b2 = 289 – 225
b = 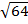
b = 8cm
∴ r2 = 82+ 82
r2 = 64 +64
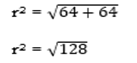
∴ r =11.31cm
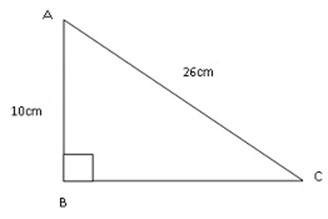
2. Given triangle ABC, where B = 900.Find the lengths of the sides which are not given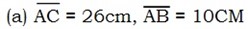
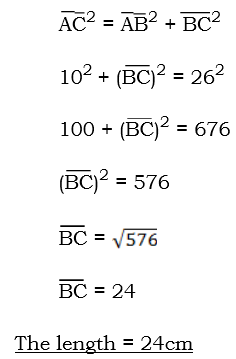
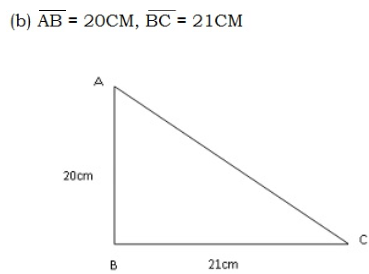

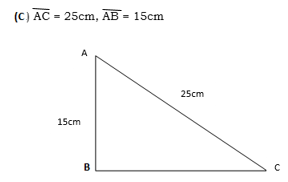

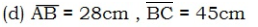
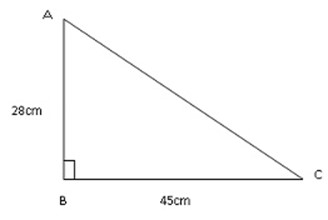
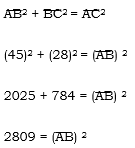
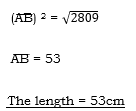
3. A man travels 15km due north and then 8km due west. How far is he from his starting point?
Solution:
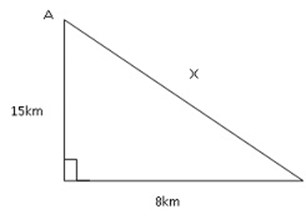
X2 = 152 +82
X2 = 225 +64
X = 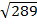
X = 17km
∴ He is 17km from his starting point
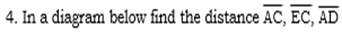

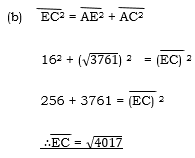


Find the area of the triangle and the length of the perpendicular from C to B.
Solution: