Similar figures:
Two polygons are said to be similar if they have the same shape but not necessarily the same size.
When two figures are similar to each other the corresponding angles are equal and the ratios of corresponding sides are equal.
SIMILAR TRIANGLE
Triangle are similar when their corresponding angles are equal or corresponding sides proportional consider the figure below :
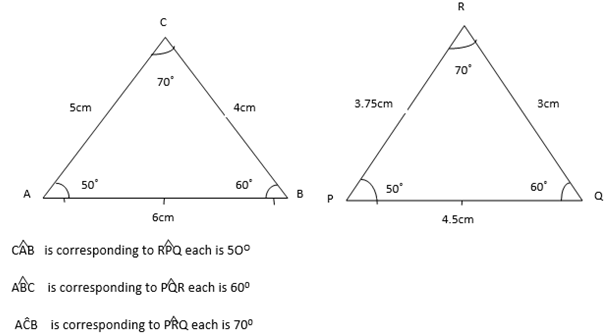
Since corresponding angles are equal then the two triangles are similar
Also: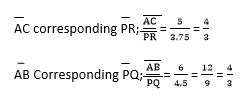
Since the ratio of corresponding sides are equal then the two triangles are similar
Note
(
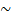) is a sign of similarity, from above 
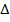ABC 
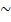
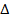PQR
Examples
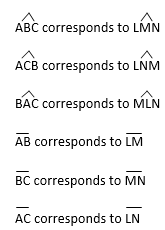
1. Given that 
SLK
NFR, identify all the corresponding angles and corresponding sides
Solution:
Corresponding sides;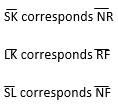
3. One rectangle has length 10cm and width 5cm. The second rectangle has length 12cm and width 4cm. Are the two rectangles similar? Explain
Solution:
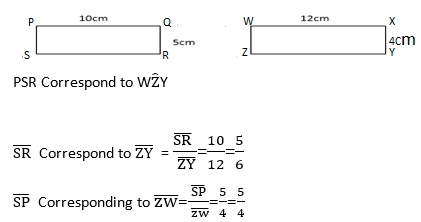
Therefore; the two rectangles are not similar because the ratio of corresponding sides are not proportional
4. A rectangle has length 16cm and width 23cm, A second rectangle has length 12cm and width 9cm. Are the two rectangles similar? Explain
Solution:
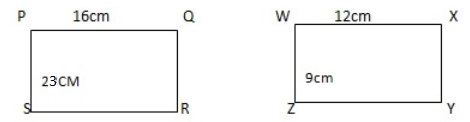
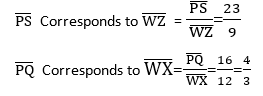
Therefore;The rectangles are not similar because the ratio of corresponding sides are not proportional
Conditions for two triangles to be similar;
1. Corresponding angles are equal or corresponding sides proportional
For other polygons
– Corresponding angles equal and corresponding sides proportional
QUESTIONS:
a) Given that 
PQR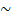 
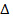LMN and that 
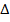PQR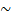
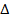ABC identify the corresponding angles and sides between 
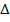ABC and 
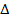LMN.
solution
Exercise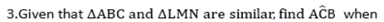 
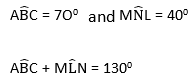
Solution:
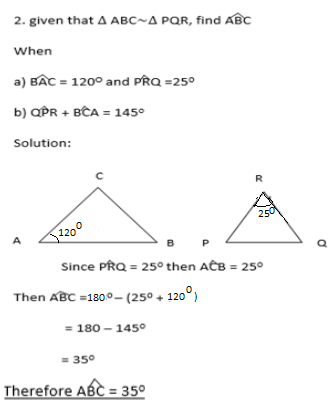
a) ABC = 70O ,MNL = 400 ,ACB =?
a) Name the triangles which are similar
b) Identify the corresponds angles
Solution:
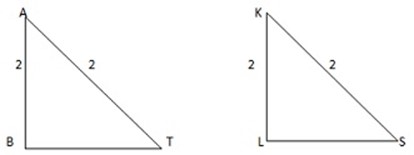
The triangles ABT and KLS are similar
8. Name the triangles which are similar to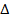 
ADC
10. Which of the following figures are always similar?
a) circles d) Rhombuses
b) Hexagons e) Rectangles
c) squares f) Congruent polygons
Solution:
The figures which are always similar
a) circles
b) squares
Exercise 1
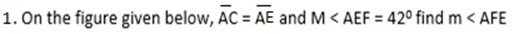
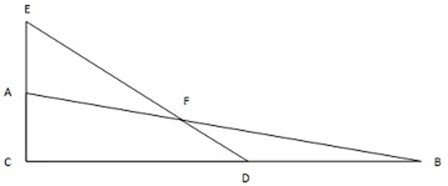
M < AEF = 420
M < AFE =?
900 – 420 = 480
M < AFE = 480
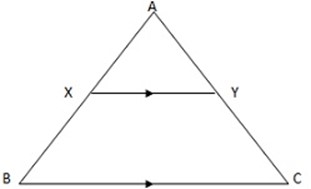
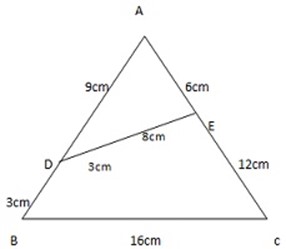
INTERCEPT THEOREM
A line drawn parallel to one side of a triangle divides the other two sides in the same ratio
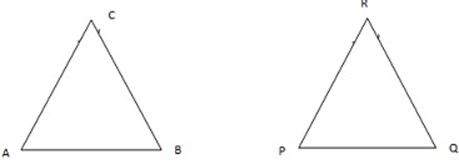
AAA – Similarity theorem
If a correspondence between two triangles is such that two pairs of corresponding angles are equal then the two triangles are similar
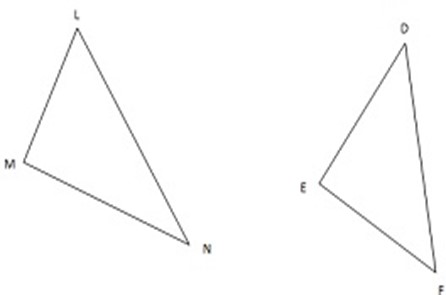
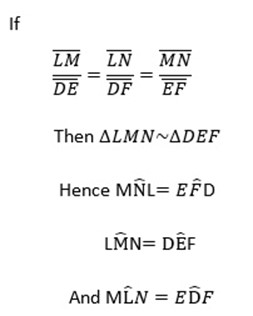
SSS – similarity Theorem
If the two triangles is such that corresponding sides are proportional, then the triangles are similar
SAS – Similarities theorem
If the two triangles is such that two pairs of corresponding sides are proportional and the included angles are congruent then the triangles are similar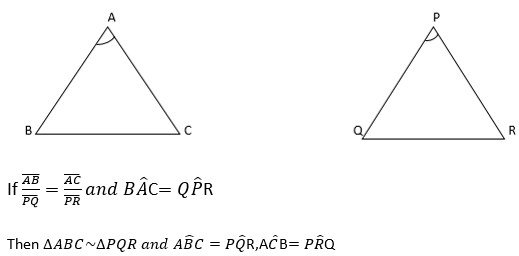
PROPERTIES OF SIMILAR TRIANGLES
From the previous discussion, properties of similar triangles can be summarized as:-
1. Corresponding angles of similar triangles are equal
2. Corresponding sides of similar triangles are similar
3. Two triangles are similar if two triangles of one triangle are respectively equal to two corresponding angles of the other
4. Two triangles are similar if an angle of one triangle equals an angle of other and the sides including these angles are proportional.
ENLARGEMENT
Scale enlargement
Scale – is a ratio between measurements of a drawing to the actual measurement.
It is normally started in the form 1: in example if a scale o a map is 1: 20000, then 1 unit on the map represents 20000 units on the ground
Scale =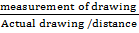 
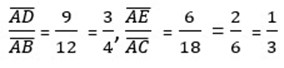
Examples of scales
1. Find the length of the drawing that represents
a) 1 stem when the scale is 1:500,000
Solution:
1:500,000 means 1 cm on the drawing represents 500,000 cm on the actual distance
= 
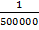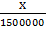
500,000x = 1500,000
X =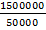 
X = 3cm
The drawing length is 3cm
b) 45km when scale is 1cm to 900m
Solution:
Scale = 1: 90000
Scale =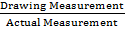 
X =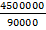 
The drawing distance is 50cm
2. Find the actual length represented by
a) 3.5cm metres when the scale is 1: 5000m
Solution:
Scale =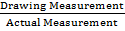 
= 
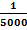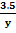
y = 5000 x 3.5
y = 17500cm
y =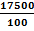 
= 175m
The distance is 175m
b) 1.8mm when the scale is 1cm to 500metres
Solution:
Scale =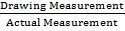 
= 
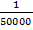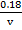
v= 0.18 x 50000
v = 9000cm
v = 90m
The actual length is 90m
Exercise:
1. Find the length of the drawing that represents
a) 200m when the scale is 1cm to 50meters
Scale =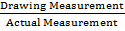 
=
= 
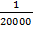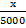
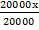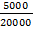
X = 4cm
The length of drawing = 4cm
b) 1.5 when the scale is 1cm to 100metres
= 
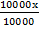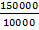
x = 15cm
The length of drawing = 15cm
d) 1600km when the scale is 1mm to 1km
=
= 
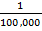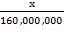
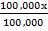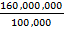
x = 1600km
The length of drawing is 1.6 mm
e) 10m when the scale is 1: 500
= 
= 
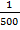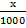
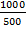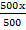
x = 2cm
The length of drawing= 2cm
2. Find the actual length represented by
a) 13.15mm which the scale is 1: 4000
Scale =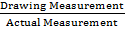 
=
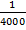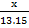
x = 0.0032875mm
b) 3.78cm when the scale is 1mm to 50km
= 
= 
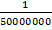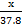
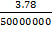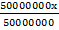
x = 0.0000000756
3. On a scale drawing the length of a ship is 42cm. If the actual length of the ship is 84cm, what is a scale if width of the ship is 23cm, what is the corresponding width of the drawing?
Solution:
Scale =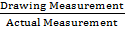 
=
= 
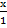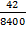
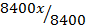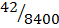
x = 1:200
Scale = 1:200
=
= 
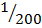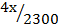
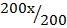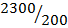
x = 11.5cm
The corresponding width of drawing = 11.5cm
ENLARGEMENT
When two figures are similar, one can be considered the enlargement of the other
(a)
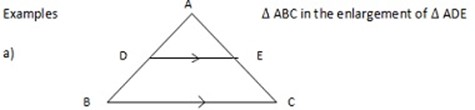
b) Square ABCD is the enlargement of PQRS
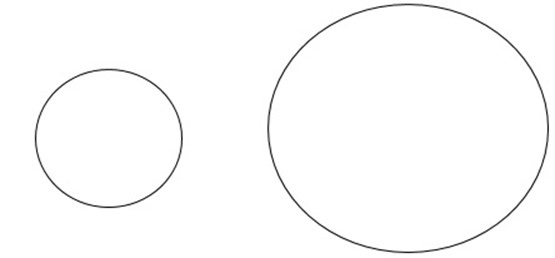
c)The larger circle is the enlargement of smaller circle
Example
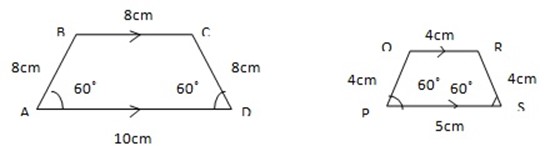
1. State whether ABCD is the enlargement of PQRS
Solution:
Since the correspond side are in the ratio 0f 2:1 and corresponding equal then ABCD
PQRS
Scale factor:
If two polygons are similar and the ratio of their corresponding sides is 5:3, then the enlargement scale is 5/3
Example
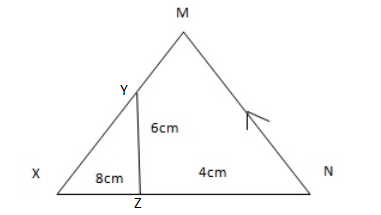
Find the scale of enlargement hence calculate
Solution: 
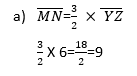
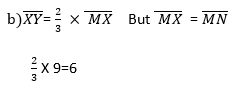
Scale factor for areas
If two polygons have a scale factor of K then the ratio of the areas is K2
Example
If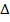 
ABS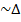
VST and the area of 
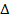STV is 6 square cm. find the area of 
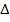ABC
Exercise
1. Two triangle are similar but not congruent. Is one the enlargement of the others one triangle is the enlargement of the other
2. The length of rectangle is twice the length of another rectangle. Is one necessary an enlargement of other. Explain? No, Since the width are not necessarily in the same proportional as the lengths.
3. In figure below, show that 
PQR is not an enlargement of 
DEF
= 
= 
, 
= 
= 
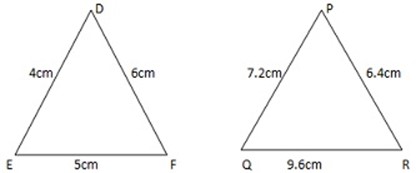
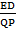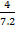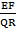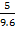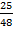
PQR is not enlargement of 
DEF
5. Triangle XYZ is similar to triangle ABC and XY = 8cm. If the area or the triangle XYZ is 24cm2 and the area of the triangle ABC is 96cm2, calculate the length of AB.
