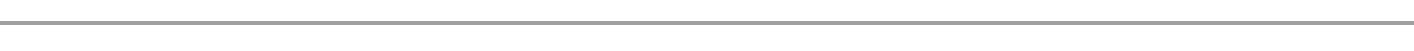DIVIDE CIRCLE/PIE CHART
Is a divided circle which drawn show the nglish-swahili/distribution” target=”_blank”>distribution of item or items in terms of degrees.
In drawing divide circle all items values must be converted into degree values.
Total degrees of a circle =3600
| 3600 = 100% |
edu.uptymez.com
Construction of Divide circle
Example:- carefully study the table below which show the use of soft drinks at chapamaji village in crates
| Type of soft drink | Coca | Fanta | Pepsi | Mirinda | Novida |
| Number of crates | 300 | 150 | 250 | 100 | 200 |
edu.uptymez.com
a) Draw pie chart to present data above
b) Give merits and demerits of the method you use (a in “a” above)
Solution
Procedures to draw a pie chart
i.To find total of items
Total = Sum of all items (soft drinks) consider the table below:
| Soft Drink | Coca | Fanta | Pepsi | Mirinda | Novida | Total |
| Number of crate | 300 | 150 | 250 | 100 | 200 | 1000 |
edu.uptymez.com
Total = 300+ 150 + 250 + 100 +200
=1000 crates.
ii. Step:- To change each type of soft drink into degree values.

iii.To draw pie chart. Drawing pie chart the obtained angles inserted in a circle by using protractor.
DIVIDE CIRCLE TO SHOW THE DISTRIBUTION OF SOFT DRINKS
- Merits of pie chart
edu.uptymez.com
i. It is simple to construct.
ii. It is easy to interpret as they use both degree and percent
iii. It gives visual idea as the shades us
iv. It does not hide other feature when left unshaded
v. It has wide variety of uses in geographical field.
vi. It is useful to compare regions of high and low production.
Disadvantage of Pie Chart.(demerits)
i. It involve some mathematical calculation i.e difficult to construct.
ii. When drawn in percentage become difficult to interpret.
iii. It is time consuming
iv. It is difficult to select shade textures for many items
v. It is difficult to read exact values because reference can be made to a scale
Importance of statistics
- Helps in the comparison of different geographical phenomena for example climate, population, commodity and production.
- Used to summarize raw and bulk data for easy interpretative and visual explanation.
- It facilitates land use planning
- Helps resources allocation and provision of social services for example food, health, water, education.
- Makes it easy to compare data
- Its knowledge simplifies research activities
edu.uptymez.com
SUMMARIZATION OF MASSIVE DATA
Raw data collected from various sources does not tell users much unless they are organized in summary form. This process of summarizing data in an organized form makes sense out of the scored information.
This brings the necessity to geographer’s of summarizing massive data which could be done in the following ways:-
- Frequency nglish-swahili/distribution” target=”_blank”>distribution
edu.uptymez.com
Frequency nglish-swahili/distribution” target=”_blank”>distribution help to determine how many times a certain scores are arranged/occurs in that presentation. The technique consist of a table in which different scores are arranged in their rank order. It is advised ti start with the highest/largest value and back to the smallest That is in descending order
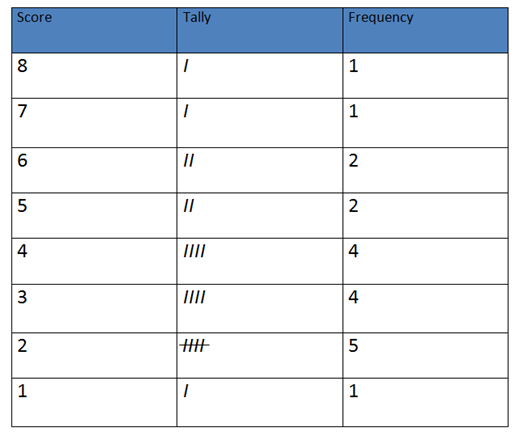
E.g: Use the data below which express a population survey in a certain region
- The raw information found that the family size of 20 families interviewed was 3,2,2,4, 3, 7, 8, 1, 3, 6, 2, 2, 4, 5, 6, 4, 3, 4, 5 and 2
- Arrange the scores in lending order from 8 to 1
- Distribute each score in the representation to get how many times each score occurs. This process of nglish-swahili/distribution” target=”_blank”>distribution is called tallying
edu.uptymez.com
Distribution of the score to get their frequency
The frequency which means the number of times a score or event appears or occurs is obtained. At time one is confronted with a large number of scores or event involving a whole region this is certainly difficult to handle if one deals with each score or event separated. The world is made simpler and easy by the use of grouped frequency. Be low are the steps involved in making grouped frequency.
Decide the size of the class interval. This is actually the number of scores or events in each class. But is important to know the characteristics class internal in order to be able to make classes.
a) A score appears only once. That means no score should be long to more than one class.
b) The size of the class intervals should be uniform
c) The class intervals should always and be continuous
d) The range of class intervals should be between 3 and 20. Thus, the intervals should not be below 3 and above 20.
e) Decide on the number of class intervals needed.
f) Ensure that the class intervals are the same size.
Ensure that no score falls in more than one class interval. Arrange the class intervals in order of ranks preferably in a descending order.
From the summarized data above one can identify two concept.
i) Apparent upper limit
ii) Apparent lower limit
These limits are the values which are seen in each class internal. The apparent lower limit opens the class interval while the apparent upper limit close the class interval.
Presentation of frequency
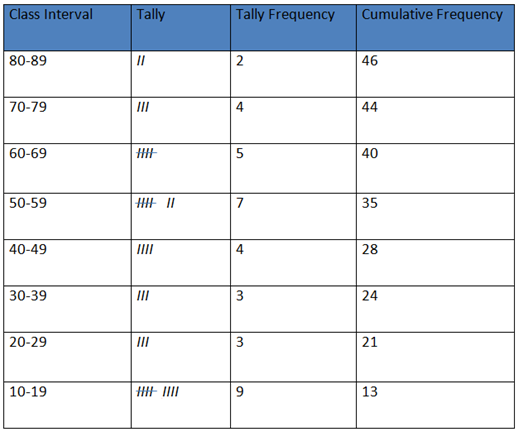
The table shows 80, 70, 60, 50, 40, 30, 20, and 10 as apparent lower limits and 89, 79, 69, 59, 49, 39 29, 19 and 9 as the apparent upper limits
A part from the two concepts above the table also has real limits which are not visible which are 0.5 below or above the apparent limits.
From the summary made above one can obtain other measures of statistics. Such measures include:-
I. Measure of central tendence
II. Measure of dispersion (variability)
III. Measure of relationship (correlation)
IV. Measure of relative position
SOURCES OF STATISTICAL DATA
a) Primary source
Data are collected from the field. These are original data for example through mail, questionnaire, interviews, observations, survey etc
b) Secondary source
Data are collected in official sources such as bureau of statistics, census and surveys, government publications, ministry bulletin, individual research work.
TYPES OF DATA
Individual data
Are exact value given to individual,
For example production of certain commodity, Population etc.
Discrete data
Are whole numbers assigned to certain item
E.g. 3 people
- 10 trees
- 1 shop
edu.uptymez.com
Continuous data
Are data with specific / exact value for example;
- Temperature
- Weight
- Distance
edu.uptymez.com
Grouped data
Are data without specific /exact figures groups of several value are used
E.g.
- 0 – 9
- 10 -19
- 20 – 29
edu.uptymez.com
PRESENTATION OF MASSIVE STSTISTICAL DATA
When statistics are collected in the field, they are usually in a haphazard form. For the statistics to be useful they need to be processed, arranged in logical manner and presented in such a way that they information can be easy to read and make conclusion.
For this purpose, statistics may be arranged in tables. From the tables the data may be presented in graphical form using graphs and charts.
This include the line and bar graphs as well as proportional circles and pie charts. Statistical data could also be presented in a forms of map i.e flow line maps, dot maps and choropleth maps.
SIMPLE STATISTICAL MEASURE AND INTERPRETATION
Measure of central tendency – Refers as indices of central locations in the nglish-swahili/distribution” target=”_blank”>distributions these are measures of average a typical performances of geographical aspect especially crop production crop sales, marketability, population sizes and others
These are three measure of central tendency, namely the mean, mode and median
a) The Arithmetic mean
The average is what we call Arithmetic mean. Arithmetic mean refers as the sum (total) of all scores or events divided by the number of occurrences. Mathematically arithmetic mean is represented as

For example
50, 90, 70, 60, 80, 75, 65, 60, 80, 70 compute the Arithmetic mean of the above geography marks

This is the normal or average pass mark of the students is 70 percent.
b) MODE
Mode is the most frequent score in a data nglish-swahili/distribution” target=”_blank”>distribution. It is the score or value which occurs more times than any other score or value in a nglish-swahili/distribution” target=”_blank”>distribution.
Example
2, 7, 8, 9, 2, 3, 1, 3, 2, the mode in the nglish-swahili/distribution” target=”_blank”>distribution is 2 which occurs 3 times. But sometimes the nglish-swahili/distribution” target=”_blank”>distribution is shown in a form of grouped data.
Mode becomes useful in statistics in many whys but one of the important whys is when mode is used to describe the content of the nglish-swahili/distribution” target=”_blank”>distribution of data.
Note: sometimes we may have two modes (bimodal) or more than two.
Median
Median can be defined as the score or value which is most central in the nglish-swahili/distribution” target=”_blank”>distribution of data or the mid point (middle value) in a nglish-swahili/distribution” target=”_blank”>distribution or set if score. The set of scores can be in odd or even form.
⇒Suppose the data nglish-swahili/distribution” target=”_blank”>distribution is odd and simple as shown below:
3, 4, 11, 12, 3, 1, 2, 6, 2.
Median is obtained through the following steps
a) Arrange the score in either descending or an ascending orderEg: 1, 2
b) Locate the central most score, where as: from the above data mid score is 3 so that the median is 3
⇒Suppose the data nglish-swahili/distribution” target=”_blank”>distribution is simple but even the median is obtained through the following procedures given the nglish-swahili/distribution” target=”_blank”>distribution below:
15, 13, 3, 7, 4, 6, 11, 9
a) Arrange the data in descending/ascending order 3, 4, 6, 7, 9, 11, 13, 15
b) Observe the mid point which is either for 9.
c) Get the median by calculating as follows.

The median is therefore at position 4 in either way. From left of the scores, 4 the score is 7 while the right it is 9.
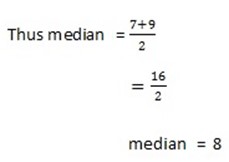
The significance of median is to reveal the position where the data set is made to neutraize the weakness of Arthmetic mean as na average which is influenced by extreme score.
The three measures of central tendency can be combined in data interpretation. This is as follow.
a) When mean, mode and median are the same value, nglish-swahili/distribution” target=”_blank”>distribution is normal. The pheramena observed biasness.
b) If they are not of the same value, the nglish-swahili/distribution” target=”_blank”>distribution is normal hence there is biasness
Measures of central tendency can be calculated from grouped data.
Example.
| SCORES | FREQUENCY |
| 0 – 4 | 2 |
| 5 -9 | 6 |
| 10 -14 | 10 |
| 15 -19 | 8 |
| 20 -24 | 4 |
edu.uptymez.com
Assumed mean = 12
| C1 | F | X | Real limits | D =x -4 | fol | cf |
| 0 -4 | 2 | 2 | 0.5 – 4.5 | -10 | -20 | 2 |
| 5 – 9 | 6 | 7 | 4.5 -9.5 | -5 | -30 | 8 |
| 10 – 14 | 10 | 12 | 9.5 -14.5 | 0 | 0 | 18 |
| 15 – 19 | 8 | 17 | 14.5 – 19.5 | 5 | 40 | 26 |
| 20 – 24 | 4 | 22 | 19.5 – 24.5 | 10 | 40 | 30 |
| Efd = 30 | ||||||
edu.uptymez.com



Measure of central tendence can be calculated from a grouped data
Example
| Scores | Frequency |
| 0-4 | 2 |
| 5-9 | 6 |
| 10-14 | 10 |
| 15-19 | 8 |
| 20-24 | 4 |
edu.uptymez.com
Assumed mean =12
| Cl | f | x | Real limit | d=x-A | f d | c f |
| 8-4 | 2 | 2 | 0.5-4.5 | -10 | -20 | 2 |
| 5-9 | 6 | 7 | 4.5-9.5 | -5 | -30 | 8 |
| 10-14 | 10 | 12 | 9.5-14.5 | 0 | 0 | 18 |
| 15-19 | 8 | 17 | 14.5-19.5 | 5 | 40 | 26 |
| 20-4 | 4 | 22 | 19.5-24.5 | 10 | 40 | 30 |
edu.uptymez.com
∑fd=30