Form 3 Mathematics – CIRCLE

DEFINITION AND PROPERTIES OF A CIRCLE

A circle can be defined in two ways.

A circle: Is a closed path curve all points of which are equal-distance from a fixed point called centre OR

– Is a locus at a point which moves in a plane so that it is always of constant distance from a fixed point known as a centre.

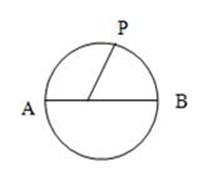
O – Is called the centre of the circle.

OP – Is the line segment is the radius.

AB – Is the line segment of diameters of the circle.

O – (Centre) – Is a fixed point of circle.

OP (Radius) – Is the constant distance from the centre to any point on a circumstance of a circle.

AB (Diameter) – Is a line segment which passes through the centre of a circle.

A circumference – Is a length of a locus which moves around the centre.

Diameter =2 x Radius

             D = 2r

Hence the diameter of a circle is equal to two times radius.

            

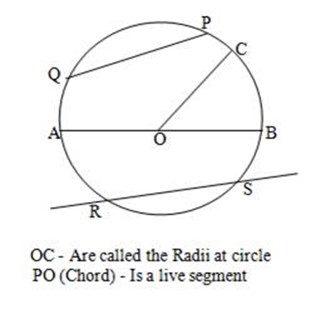
RS (Secant) – Is a line segment whose points are on the circle.

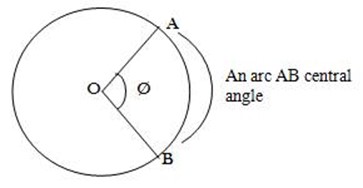
BOC – Is called a central angle

(PTQ) – A Segment – Is the part of a circular region included within the chord and its arc.

(COB) Sector – Is the part of a circular region bounded by two radii and an arc.

CENTRAL ANGLE

Consider a circle of radius r, length of arc l, subtending a central angle.

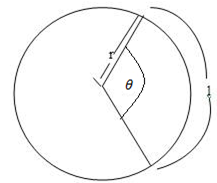
– The length of the circumference C of the circle is C = 2πr. This means that the length of the arc intercept by a central angle 360º is 2πr.

– The length of an arc is proportional to the measure of the central angle of the central angle. Thus if the central angle is 1

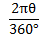
 Example 1.

An arc subtends an angle of 20⁰ at the centre of a circle of radius 25m.

Find the length of the arc.

Length of an arc is given by

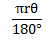
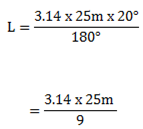
= Length of an arc = 8.72m

An arc of length 5cm subtends 50º at the centre of a circle. What is the radius of the circle.

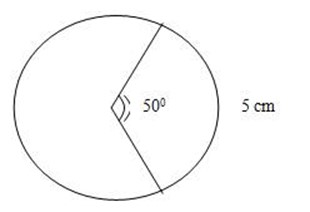
Data

θ = 50º

Length = 5 cm

Radius = required

Length of an arc is equal to

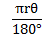
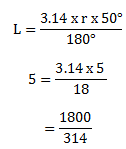
         =5.73cm

Example 3

A circular running track has radius 50m. A sprinter runs 100m along the track.

Through what angle has she turned?

 

Radius = 50m

Length of an arc = 100m

θ = Required

Length at an arc is equal to

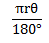
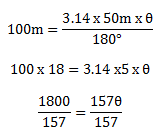
 The central angle is 114 .650

Questions:

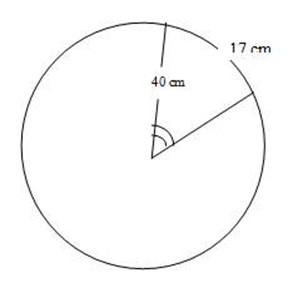
1. An arc subs tends 25 at the centre of a circle of radius 40m. What is the length of the arc?

Data

Length of an arc = required

Radius = 40m

θ =- 25

Length at an arc is equal to


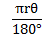
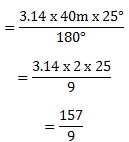
The length at an arc = 17.44m

2. An arc of length 17cm forms a circle of radius 40cm what angle does the arc subtend?

Data :-

Length of an arc = 17cm

Radius = 40cm

θ= Required

Length of arc is equal to

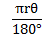
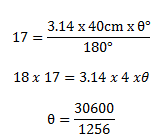
The arc subtends 24.330

3. An arc of length 16m subtends 400 at the centre of the circle. What is the radius at the circle?

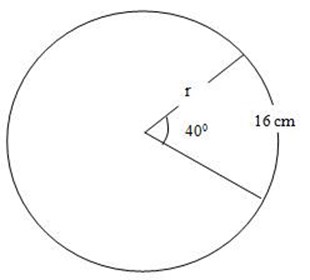
Data

Length an arc = 16m

Radius = Required

θ = 40⁰

Length of arc is equal to


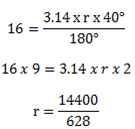
The radius = 22.85m

RADIAN MEASURE

Angles can also be used to measure the amount of turning. Turns of a minute hand of a clock and a wheel can be measured in both angles and radians. Example a minute hand of clock turns through an angle of 90º 0f ½ π radians between noon and 12:15pm as shown in the figure.

– The tip of the hand has covered a distance of ½ π radians.

From noon to 12:45 pm, the hrs turned through an angle of 270ºor 3/2πr radians. The angle 270º is reflex angle.

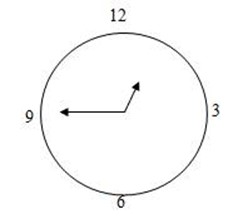
– One complete turn at hand clock represents an angle of 360º or 2π radians.

– Measures of angles more than 360⁰ or 2 π radius can be obtained if hand of a clock measures more than one complete turn. Example from noon to 1:15 pm, the hand has turned through 1 ¼ turns. Now one turn is 360⁰ or 20 radians.

– 5/4 turns or 3600 x 5/4 0r 2π x 5/4 radians which reduce to 450º 0r 5/2π radians.

– There fore from noon to 1:15 pm the hand turns through 450º or 5/2π radians.

Questions

1. Give the size in degree at an angle through which a minute hand of a clock has returned between noon and the following times.

 (a) 12:40

Solution:

1min = 6

40min =?

X= 40min x 6

X = 240

(b) 3:00

Solution

1hour = 360

3 hour =?

X = 3 hour x 360⁰

X = 1080⁰

(c) 9:00

Solution

 1hour = 360⁰

9 hour =? X

X = 9 x 360⁰

X = 3240⁰

2. Give the size in radians at angles through which the minute hand of a clock has turned between noon and the following times.

(a) 12:20pm

Solution

 1min = 6⁰

20 min =? X

X= 20min x 6

X = 120⁰

πrad = 180º

                                  ? = 120º

x = π rad x 120

X = 2/3 π rad

(b) 2:15

Solution

1hour = 60 min

2 hour =? X

x =60 x 15min

X =120
120 x 6º=720º
= 720⁰ +90^º
              = 810º

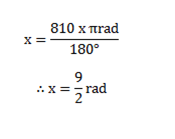
(c) 24:00 noon

Solution

1 hour = 360⁰

24hrs = ?

X = 360⁰ x 20

             = 8640⁰

πrad = 180⁰

?x = 8640⁰

x = 8640⁰ x πrad
 

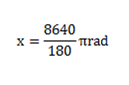
X = 48πrad

 RADIAN MEASURE

– The relation between the arc length l, the central angle θ, and the radius r, can be used to compare the measurement of an angle in radius with the measurements in degree.

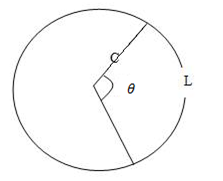
Circumference of the circle for the given radian C = 2πr. Circumference sector

But C = length at an arc

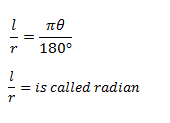
In abbreviation is written as:-

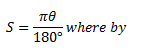
S = is radian measured of an angle

θ = is the degree measure

θ= 17 .19⁰

The angle in degree is 17. 19⁰

Class Activity:-

1.Find the degree of each of the following :-

(i) 3/2π

Solution:-

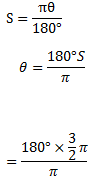
 = 90⁰ x 3

= 3/2π = 270⁰

(ii)   ¾π

Solution

                       

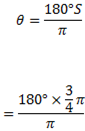
¾  π = 135⁰

Example 1:

Find in radian as multiple of π for each of the following degrees.

(a) 315⁰ (b) 240⁰

Solution:

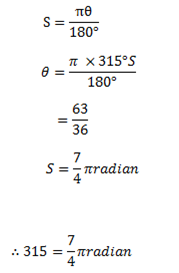
(b) 240⁰

Solution:-

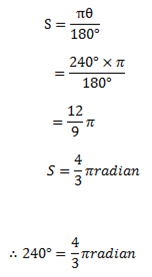
2.                  Change the following radians into degree

(a) 0.3 (b) 5

solution

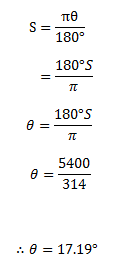
Class activity.

1. Find the degree of each of the following

ⁱ⁾ 3/2π

Solution.

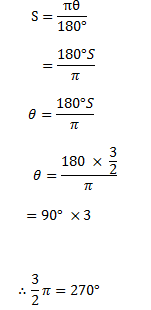
ii 3/4 π

Solution

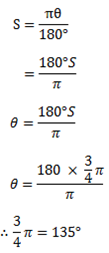
iii) 2 π

Solution

2.Find the radians multiple of the  π following

(i)80°
Solution

 

ii) 215º

Solution

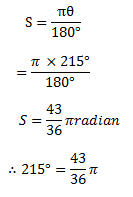
iii) 60⁰

Solution

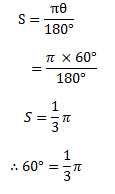
3. (i) Change the radians into the degree of 0.3 

 

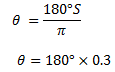
∴The angle the degree = 54⁰

(ii) 5
Solution

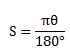
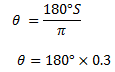
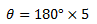
The angle degree = 900⁰

ANGLES IN CYCLIC QUADRILATERAL

These are four angles whose vertices are lying on the circumference of a circle.

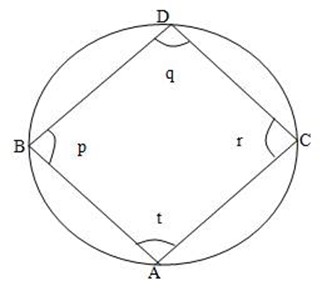
The angles p, q, r, and t are called cyclic angles in a quadrilateral ABCD, q and t, p and r are opposite angles.

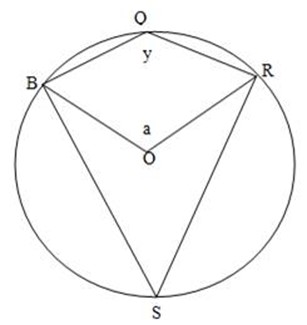
1. THEOREM:

The opposite angles of a cyclic quadrilateral are supplementary (add up to 180⁰).

Given; A quadrilateral SPQR inscribed in a circle centered at 0

Required to prove: x+ y = 180⁰

Constuction; join OR and OP

Proof: in the above figure

a = Zx (angle s on a circle) PQR)

b = Zy (angle on arc PSR)

a+b = Zx + 2y but a+ b = 360º

360⁰ = 2 (x+y ) divide by 2 both sides

x+y = 180⁰

∴ x+ y = 180º hence proved.

Example:

Find the size of each lettered angle.

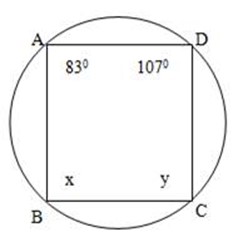
The opposite angles A and C, B and D

:. x +83⁰ = 180⁰

y = 180⁰ – 83

y = 97⁰

x+107⁰ = 180⁰

x= 180⁰ – 19

x = 63⁰

2. THEOREM:

Any inscribed angle in a semicircle is a right angle.

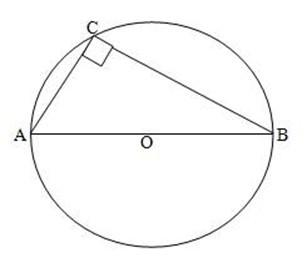
Given

AB – Is a diameter at a circle.

O – Is the center.

C – Is any point on the Circumference

Required to prove that ACB = 90⁰

2 ACB= AÔB (Angle at the centre)

But,

AÔB = 180^o (Straight angle)

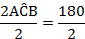
ACB = 90^o Hence proved.

Example:

Calculate the Value of x

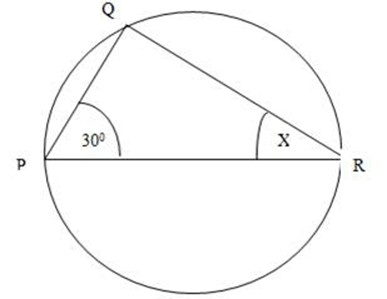
Soln:

PQR = 90^o (Angle in a semi Circle)

Then 90^o + 30^o + x = 180^o

(Angles sum in A)

x = 180^o – 120^o

x = 60^o

An exterior angle is an angle formed outside a cyclic quadrilateral. An internal angle is formed inside the cyclic quadrilateral when you provide line from this angle you will form an angle which is outside called exterior angle.

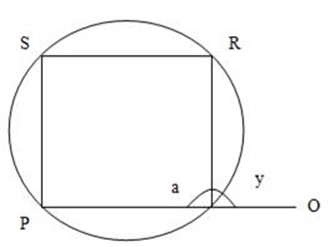
THEOREM: 3

Exterior angle of a cyclic quadrilateral is equal to the inside opposite angle.

Aim: to prove that PSR = PQT

Proof: let angle PQR = a

Angle PRS = b

Angle PQT = y

(i)      PQR + PSR = 180^o (Because it is opposite angle of cyclic quadrilateral).

Thus a+b = 180^o

(ii)    Therefore when you equate them since both are 180^o

(iii)   PQR + RQT = 180^o (Because they are adjacent angles on straight line)

Thus a + y = 180^o

Therefore when you equate them since both are 180^o you will have:

a + b = a + y

B = y

But b = PSR

And y = PSR

PSR = PQT

Proved.

THEOREM 4:Angles in the same segment are equal.

THEOREM 5: Angles in the semi circle are right angled triangle.

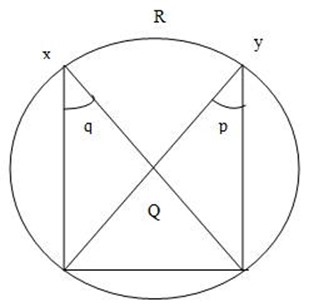
Aim: To prove that PxQ = PyQ

Construction: join OP and OQ

Let PÔQ = P

PVQ = q

PYR = r

(i)      PÔQ = 2p x Q and

P = 2q (Because angle at the centre is twice the angle at the circumference)

(ii)                PÔQ = 2PyQ (Because angle at the centre is twice the angle at the circumference)

P = 2r

x = P = 2q, P = 2r

          = 2q     = 2r

       q = r

TO ANSWER THE QUESTIONS:

1. Find the value of X. if O is the centre of Circle

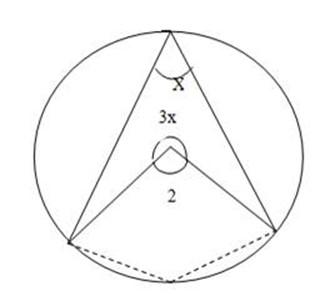
Soln:

Angle at the centre is twice the angle at the circumference.

Since the circle at the centre is 360^o

3 x + 2x = 360^o

5x = 360^o

= 72^o

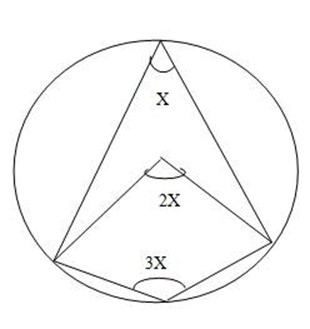
(b) Angle at the centre is twice the angle of the circumference.

Opposite angle at a cyclic quadrilateral are supplementary (add up to 180^o)

x + 3x = 180^o

      4x = 180

         x=45

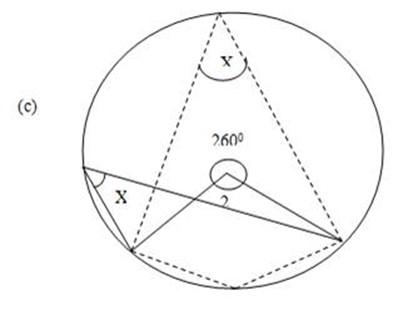
Soln:

Angle at the same segment are equal.

Angle at the centre is twice the angle at the circumference.

2 x + 260^o = 360^o

Since the circle at the centre is 360^o

2x + 260^o = 360^o

2x = 360⁰-260⁰

2x=100⁰

x = 50^o

Soln:

Angle at the centre is twice the angle at the circumference.

150^o x 2 = 300^o

Since the circle at the centre is 360^o

x + 300^o = 360^o

x = 360^o – 300

x = 60^o

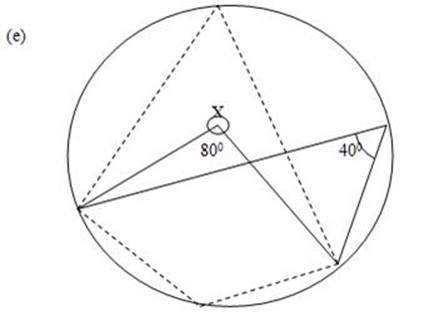
Soln:

Angle at the centre is twice the angle at the circumference.

40^o x 2 = 80^o

Since the circle at the centre is 360^o

x + 80^o = 360^o

x = 360^o – 80^o

x = 280^o

(f) Find the value of angles marked x, y and z

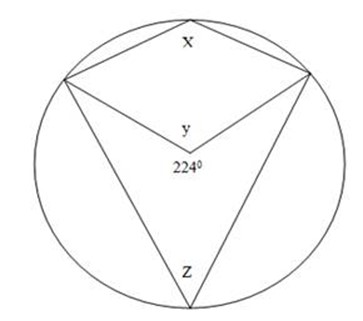
Soln:

Angle at the centre is twice the angle at the circumference.

X x 2 = 224^o

X = 112^o

Since the circle at the centre is 360^o

y + 224^o = 360^o

y = 360^o – 224^o

y = 136^o

Opposite angle of a cyclic quadrilateral are supplementary (add up to 180^o)

Z + 112^o = 180^o

Z = 180^o – 112

z = 68^o

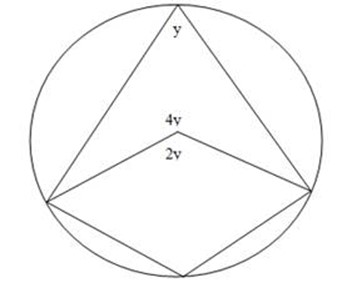
(g) Find ‘y’

Soln:

Angle at the centre is twice the angle at the circumference.

y x 2 = 2y

Since the circle at the centre is 360^o

4y + 2y = 360^o

y = 60^o

Class activity

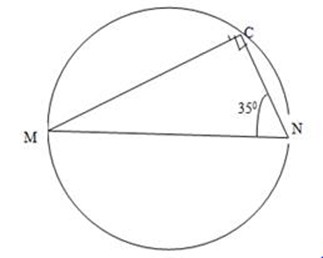
1. MN is a diameter of a circle and L is a point on the circle. If MNL = 135^o,

Find NML

Soln:

Any inscribed angle in a semicircle is a right angled triangle.
let NML=X

X + 35^o + 90^o = 180^o

X + 125^o = 180^o

X = 180^o – 125^o

NML = 55^o

2. AB is a diameter of a circle radius 10 cm and e is a point on the circumference.

CB = 12, find CA (Remember Pythagoras theorem)

Soln:

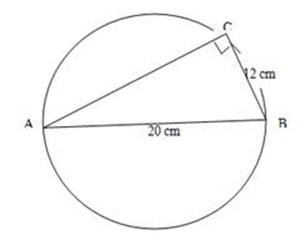
By using Pythagoras theorem

20² = CA²+ 12²

400 = CA²+ 144

CA²= 400 – 144

CA² = 256

CA= 16cm

3. AB is a diameter of a circle radius 40cm and C is point on the circumference.

If CBA = 62^O, then find CÂB

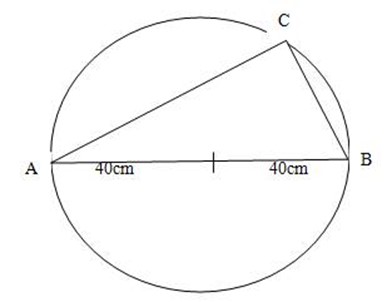
Soln:

Let X = CÂB

X + 62^o + 90^o = 180^o

X + 152^o = 180^o

X = 180^o – 152^o

CÂB = 28^o