Form 3 Mathematics – CIRCLE

THE CHORD PROPERTIES OF A CIRCLE

The chord of a circle is the line segment whose end point are on the circle. A chord which passes through the centre of a circle is called a diameter. It is very important for you to know what a chord is and how to identify the chord properties of a circle because it will summarize you with this unit.

Therefore in this section you are going to study about the chord itself and the chord properties of a circle.

You are also going to study how to develop theorem which relate to these properties at chord. At the end of the section you will be able to identify the chord, prove the theorem of the chord. Properties in a circle and then apply these theorems on solving related problems in order to identify the properties of the chord properties it easier if you draw a circle with centre O.

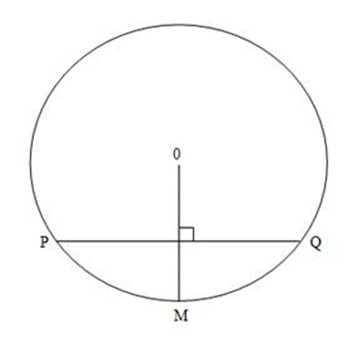
You can see that O is a centre of the OM is the radius of the circle and PQ is chord of the circle.

Therefore you will discover that.

(a) The centre of the circle lies on the perpendicular bisector of the chord.

(b) The perpendicular from the centre of the circle to the chord

(c) The line joining the centre of the circle to the midpoint of the chord.

Then from the information above you can develop the theorem which can be written as;

THEOREM

The perpendicular bisector of a chord passes through the centre of the circle.

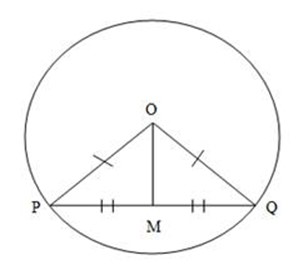
AIM: To prove that OMP = OMQ = 90^o

Construction: Join OP, OQ and OM
Proof:
(i) OP = OQ (Radii)
(ii) PN = QM (M is midpoint given)
(iii) ON = OM (common)
(iv) OPM = OQM (Bisected angles)
 

The corresponding angle are congruent and hence OMP = OMQ = 90^o proved.

THEOREM: Parallel chords intercept congruence arc.

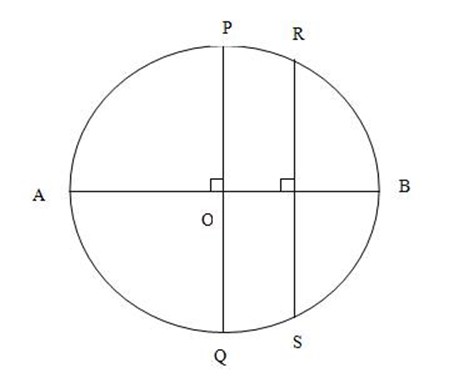
Aim: To prove that arc PR≡Are

Proof:

Arc AQ≡ Arc AP (AOB is diameter)

Arc AS≡ Arc AR (AOB is a diameter)

Arc PR ≡Arc AR – Arc AP and also

Arc QS≡ Arc AS – Arc AQ

By step (i) up to step (iii) above you can conclude that Arc PR≡ Arc QS proved

Class Activity:
Two chords, AB and CD of the circle whose radius is 13cm are equal and parallel.
If each is 12cm long, find the distance between them.
 

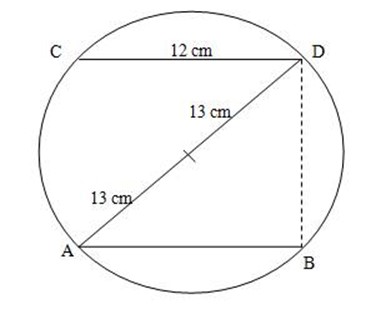
Soln: – By using Pythagoras theorem

AD²= AB² +DB²
26² =12² + DB²
676 = 144 + DB²
DB²= 676 – 144
DB² = 532
Square root both sides

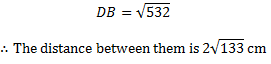
 2.A chord of length 32cm is at a distance of 12cm from the centre of a circle.
Find the radius of a circle.

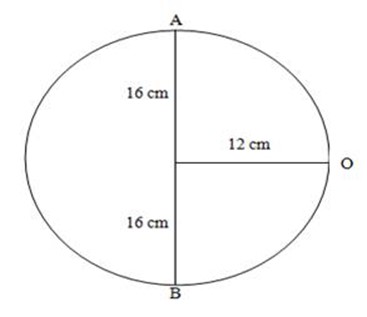
Soln:

By using Pythagoras theorem
 
AO² = 12²+ 16²
        = 144 + 256
        = 400
Apply square root both sides
 
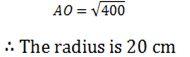
3. A distance of a chord PQ from the centre of a circle is 5cm.
If the radius of the circle is 13cm. Find the length of PQ

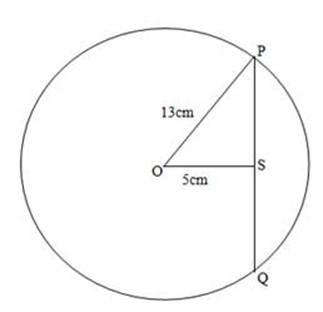
Soln:
By using Pythagoras theorem.
13² = 5² + PQ²
169 = 25 + PQ²
PQ²= 169 – 25
PQ²= 144
Apply square root both sides
PQ = 12cm
Since OS is perpendicular to PQ

Therefore PS  = SQ

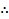PQ = 12cm + 12cm

= 24cm.

4. The chord AB of a circle with centre O radius 3cm long.

Find the distance of AB from O. give your answer in cm form

Soln:

By using Pythagoras theorem

a ² +b² =c²

15+b² =9 x 3

b² =27-15

Apply square root both sides

∴ 

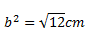
5.Two chords AB and CD of a circle with centre O. if AB = 10cm,

CD = 6cm, AO = 7cm. Find the distance between two chords

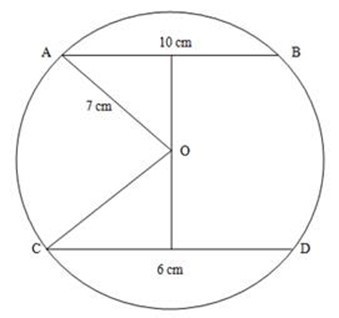
Triangle (i)

By Pythagoras theorem

a² x 6 = C²

5² + b² = 7²

25 + b² = 49

b² = 49 – 25

b² = 24

 

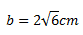
triangle (ii) by Pythagoras theorem

 a² + b² = c²

 3² + a² = 7²

 9 +a² = 49

      a² = 49 – 9

         a² = 40

Class Activity:

XY and PQ are parallel chords in a circle of centre O and radius 5cm.

If XY = 8cm and PQ = 4cm, find the distance between two chords.

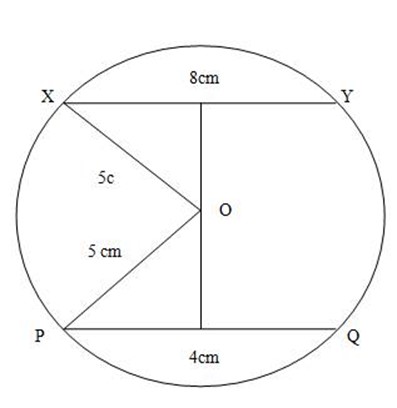
Soln:

1^st triangle

By using Pythagoras theorem.

 C² = a² + b²

 5² = 4² + b²

 25 = 16 + b²

 b² = 25 – 16

 b² = 9cm

 square root both sides

 b= 3cm

 2^nd triangle

 By using Pythagoras theorem.

 C² = a² + b²

 5² = 2² + b²

 25 = 4 + b²

 b² = 25 – 4

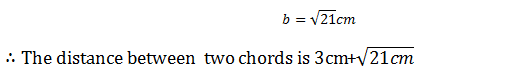
Example:

1. AB is a chord of circle with centre X. the midpoint of AB is m.

If XAB find MXA

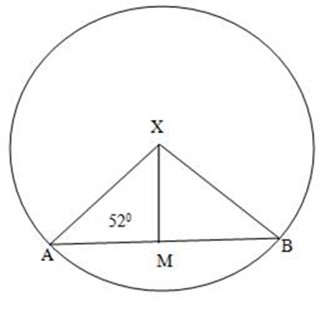
       XAM + MXA = 180^O

52^o + 90^o + MXA = 180^o

                     MXA = 180^{o –} 142º

                                = 38^o

2. AB is a chord in a circle with centre C. the length of AB is 8cm and the

Radius of the circle is 5cm. find,

The shortest distance of AB from C

ACB

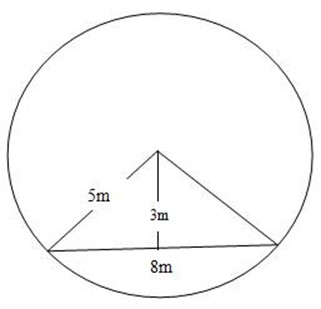
By applying Pythagoras theorem.

4² +mc² = 5²
       Mc² = 25 – 16
        Mc²= 16
Square root both sides
         Mc = 4m

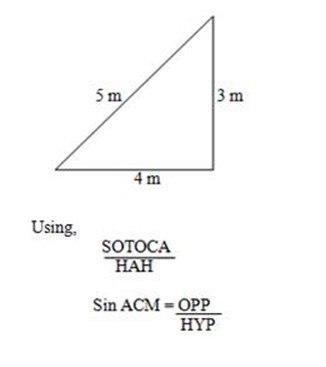
Sin ACM = 0.8000

      ACM = Sin^-1 ((0.8)

                = 53^o X 2

                = 106^o

A chord AB has length 12m. it is 7m from the centre of the circle.

Find the (a) length of AC

(b)ACB

Soln:

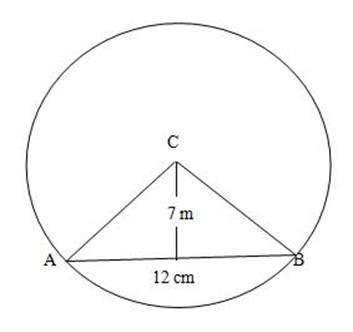
By using Pythagoras theorem.

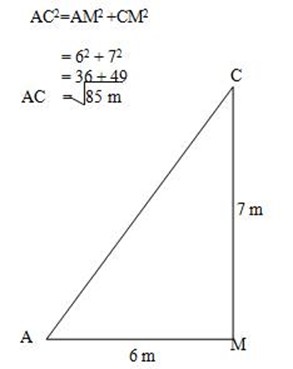
Using:

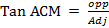
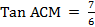
Tan ACM = 0.8571

ACM = Tan^-1

= 40^o

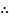ACB =40⁰ x 2

= 80^o

EXERCISE

1.                   M is the Centre at the chord AB at a Circle with centre X if

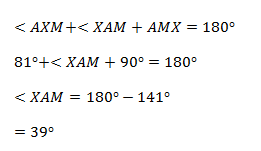
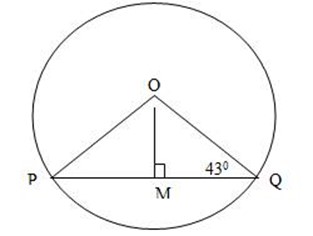
2.                   M is the centre at chord PQ at a circle with Centre O. if < PQO = 43^O. Find

 

3.                   A circle has radius 13cm and centre X. a chord AB has length 24cm. find:-

(a)                T distance of the chord from the Centre

(b)               < AXB

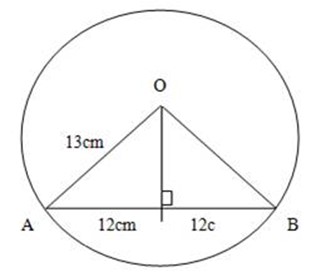
By Pythagoras theorem

(AM)² + (MX)² = (AX)²

12² + (MX)² = 132

144 + (MX)² = 169

(MX)= 169 – 144

(MX)² = 25

Square root both sides

(MX)² = 25

MX = 5cm

The distance from the centre to chord is 5cm.

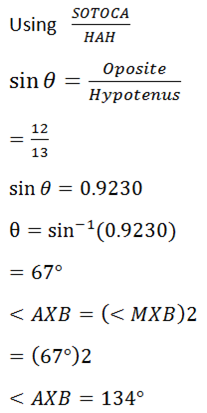
QUESTIONS:

1. Let A be the  Centre at a chord PQ at a circle with Centre O. If < PQO = 43^o, find < POQ

Soln

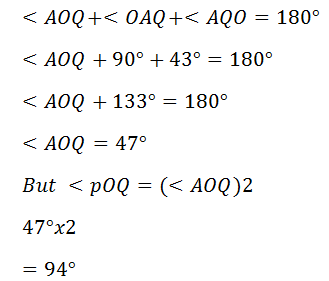
1.                   Q is the centre at a Circle and AB is a Chord

(a)                The length at AB

(b)               The distance at A from C

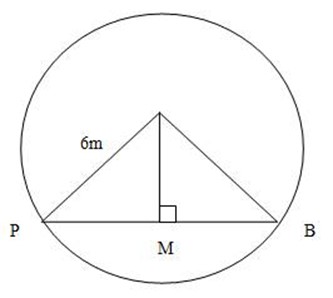
Soln:

3. PQ is a Chord in a Circle with centre R. PQ = 14cm and the distance at R from PQ is 9cm, find:-

(a)                The radius at a circle

(b)               <PRQ

Soln:

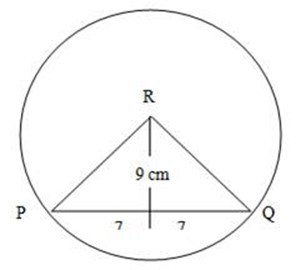
Let RQ = Radius

By using Pythagoras theorem

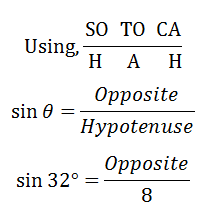
Using,      SO TO CA

H A H

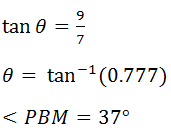
TANGENT PROPERTIES

A tangent to a circle touches it at exactly one point

THEOREM:

A tangent to a circle the line perpendicular to the radius at the point of contact.

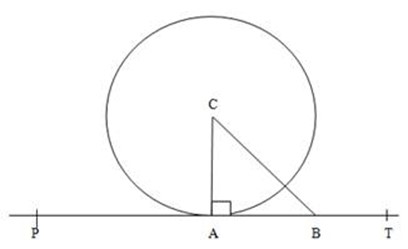
TAP is a line perpendicular to the radius CA show that TAP is a tangent as follows:-

If b is another point on TAP then CB is the hypotenuse at A CAB and hence CB is longer than CA it follows that B lies outside the Circle. Hence TAP needs the Circle only at A. TAP is a tangent to the Circle.

Hence a tangent is perpendicular to the radius.

Examples:

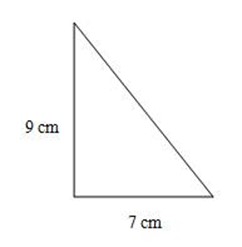
1.    TA is a tangent to the Circle with centre C. If

 Line AT⊥AC = 90°
<CAT+<ACT +<ATC=180°
90° + 49° + <ATC =180°

           139° + <ATC =180°
<ATC=180° – 139°
∴ <ATC = 41°

2.                   A point T is 8cm from the centre C of a circle of radius 5cm. Find

(a)                The length of the tangent from T to the circle

(b)               The angle between the tangent and TC

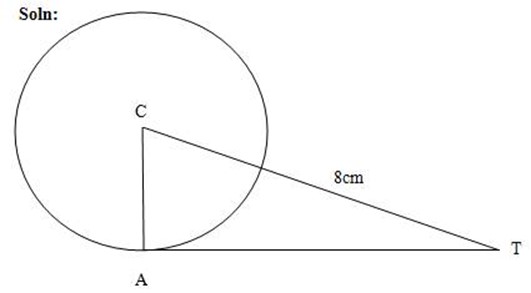
By using Pythagoras theorem

(AC)² + (AT)² = (TC)²

     5² + (AT)² = 8²

    25 + (AT)² = 64

               AT² = 64 – 25

            (AT)² = 39

                 AT = 6.24


=39º

QUESTIONS:

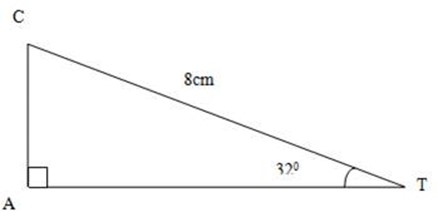
1.                   TA is a tangent to the circle at A. the centre is C. if <CTA=32º

(a)                Find <ACT

(b)               If TC = 8cm, Find AT and radius of the circle

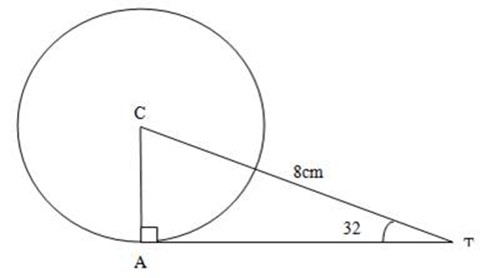
Solution: (a)

Line AT ⊥ AC = 90⁰

<ACT +=180⁰

<ACT +90⁰ + 32º =180⁰ 

                      <ACT= 180⁰– 122⁰
                     <ACT= 58⁰

Solution: (b)

               = 8 (0.5299)

           AT = 4.2392cm

2.TA is a tangent to a circle at A. The centre at the circle C if angle ACT = 73°and radius of the circle is 2m. find:-

(a)                <ATC

(b)               TA and TC

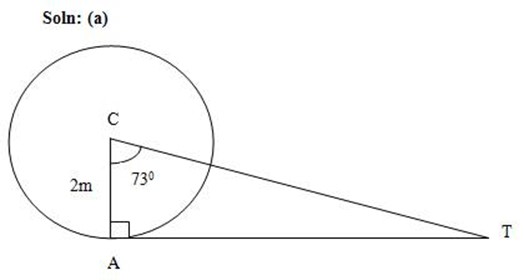
            Line TA AC = 90^{0
<ATC+<ACT +<CAT=180°
90° + 73° + <ATC =180°}

             <ATC + 163⁰ = 180⁰

                          <ATC = 180⁰ – 163^{0
<ATC =17º}

Solution: (b)
(i)

               Opp = 2 Tan 73⁰

                       =2(3.2709)

                TA = 6.5418m

(ii) By using Pythagoras theorem

TA = 6.5418m

      ≈7m

C² = a² + b²

     = 2² + 7²

     = 4+49

     c²= 53

Square root both sides

C² = 53

3. A point T is 6m form the center C of a circle radius 3cm. Find:-

(a)The length of Tangent from T to the circle

(b)The angle between the tangent and TC

Solution: (a)

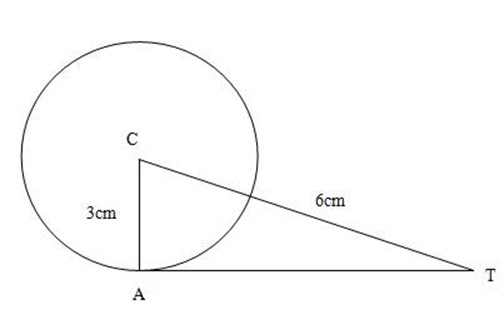
Using Pythagoras theorem

A² + b² =C²

3² + b² = 6²

9 + b² = 36

       b² = 36 – 9

        b² = 27

Square root both sides

        b² = 27

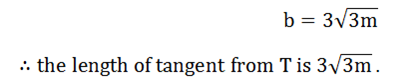
Solution: (b)

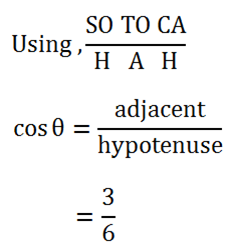
        Cos = 0.5

               = Cos -1 (0.5)

               = 30⁰

Angel between tangent and TC is 30⁰

Class Activity

1.A point, 10m from the center X of circle at radius 6m. A tangent is drawn from P to the circle touching at A. Find the length of the tangent from P to the circle.

                By using Pythagoras theorem

C² = a² + b²

10² = 6² + b²

100 = 36 + b²

b² = 100 – 36

b² = 64

Square root both sides

b² = 64

b = 8m
∴The length of the tangent from P to the circle is 8m

2.A tangent is drawn from T to a circle of radius 8cm. The length of the tangent is 4cm. Find,

(a)                The distance of T from the Centre C of the circle

(b)               The angle between TC and the tangent

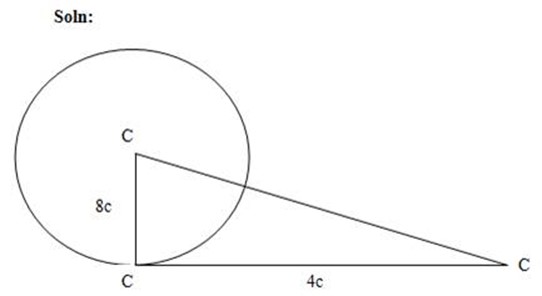
(a)     By using Pythagoras theorem

C² = a² + b²

      = 8² + 4²

      = 64 + 16

      = 80

Square root both sides

C² = 80

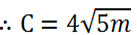
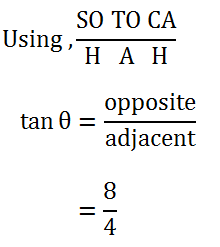
θ = tan^-1 (2)

= 6⁰

 the angle between TC and tangent is 63º

TANGENT FROM A POINT

Suppose T is outside a circle there are two tangent from T to the circle and they are equal in length

Proof:

Consider the angle TCA and TCB

CA = CB (Both are radii)
TC = TC (Common)
<TAC=<TBC

CHORD AND TANGENT

Suppose the chord CD gets shorter and shorter is that C and D approach a common point E then the chord CD becomes the tangent at E, by interesting chord theorem.

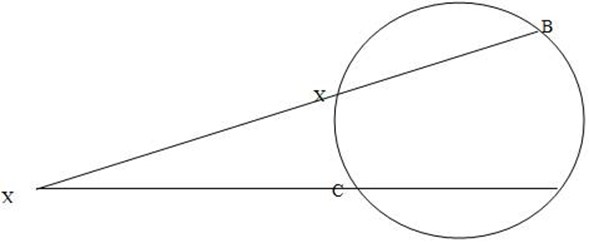
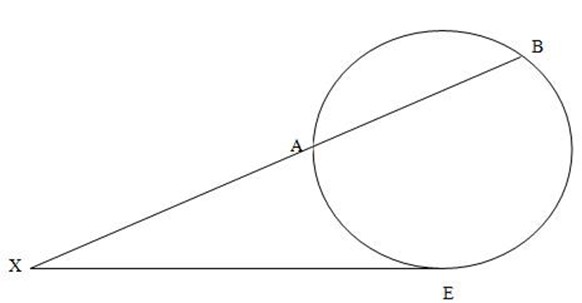
XA x XB = AC x XD

XA x XB = XE x XE

XA x XB = (XE)²

Example

1.TX is a tangent to a circle. The line TAB cuts the circle at A and B with TA = 3cm and AB = 9cm. Find TX

Solution:

(TA) (TB) = TX x TX

(TA) (TB) = (TX)²

Since, TB = (TA) + (AB)

                  = 3cm + 9cm

                  = 12cm

From the theorem

(TA) (TB) = (TX)²

3cm x 12cm = (TX)²

Square root both sides

36cm² = (TX)²

TX = ± 6cm

Since there is no -ve dimension therefore TX is 6cm

More Examples:

Find the length of unknown in the diagram.

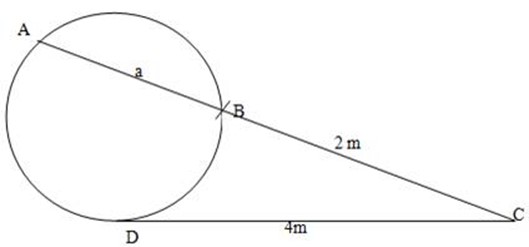
Solution:

(CB) (CA) = (DC) (DC)

(CB) (CA) = (DC)²

Since CA = (CB) + (AB)

                 = 2m + a

From the theorem.

(CB) (CA) = (DC)2

(2m) (2m +a) = (4m)²

4m² + 2ma = 16m²

         2ma = 16m² – 4m²

           2ma = 12m²
a = 6m

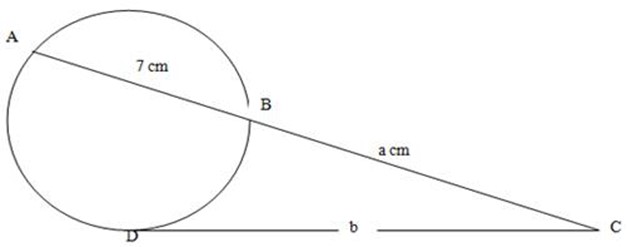
Solution:

(CB) (CA) = (CD)²

Since CA = (CB) + (AB)

                  = 9m + 7m

                   = 16

From the theorem

(CB) (CA) = (CD)²

(9m) (16m) = (b)²

Square root both sides

       144m² = b²

          b = ±12m

Since there is no -ve dimension b= 12m

2.TC is a tangent to a circle and Tab cuts at AB and B. if TA = 2cm and TB = 8cm, find TC

Soln:

From the theorem

(TA) (TB) = (TC)²

2cm x 8cm = (TC)²

16cm² = (TC)²

Square root both sides

16cm² = (TC)²

      TC = 4cm

3. TX is a tangent to a circle and TYZ cuts the circle and Y and Z. if TX= 10m and TY = 4m. Find TZ

Solution:

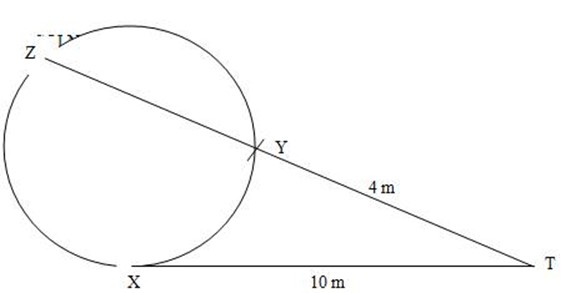
(TY) (TZ) = (TX)²

Let ZY = y

Since TZ = TY + ZY

               = 4m + y

From the theorem

(TY) (TZ) = (TX)²

(4m) (4m + y) = (10m)²

16m² + 4my = 100m²

4my = 100m² – 16m²

4my = 84m²

      Y = 21m

Since ZY = y

TZ = TY + ZY

      = 4m + 21m

      = 25m

Class Activity

1.TA is a tangent to a circle and TBC meets the circle at B and C. TA = (9cm and BC = 24cm). Find TB

Solution:

(TB) (TC) = (TA)²

  Let (TB) = y

Since TC = TB + CB

                           = y + 24cm

From the theorem

(TB) (TC) = (TA)²

(y) (y+ 24cm) = (9cm)²

Y² + 24cmy = 81cm²

Y² + 24cmy – 81cm² = 0

By using General formula

Where a = 1, b = 24, c = 81

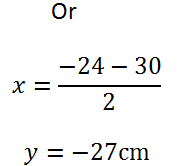
Since there is no negative dimension, the length at TB is 3cm

2.TX is a tangent to a circle and TPQ meets the circle at P and Q. TX = 12cm and PQ = 7cm, find TP

Solution:

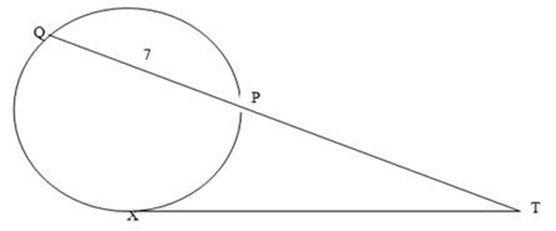
(TP) (TQ) = (TX)²

Let (TP) = Z

Since TQ = TP + QP

                 = Z + 7cm

From the theorem

(TP) (TQ) = (TX)²

(z) (z +7cm) = (12cm)²

z² + 7z = 144

z² + 7z – 144 = 0

By using the general formula

Where a = 1, b = 7 and c = -144

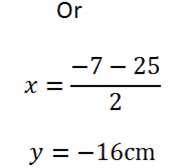
Since there is no negative dimension, the length at TP is 9cm

3.AB is a chord at a circle at length 5cm. C is another point on the circle. AB extended on the circle meets the tangents at C and T. if the TC = 6cm, find the possible value of TB.

Solution:

(TB) (TA) = (TC)²

Let

(TB) = x

Since TA = TB + AB

                 = x + 5cm

From the theorem

(TB) (TA) = (TC)²

(x) (x + 5) = (6cm)²

X² = 5x = 36

X² + 5x – 36 = 0

By completing the square

X² + 5x – 36 = 0

X² + 5x – 36 = 0

X² + 5x = 36

Add (½ b) ² both sides

X² + 5x + (½ x 5) = 36 + (½ x 5)²

X² + (5/2)² = 36 + 25/4

(x + 5/2)² = 169/4

Square root both sides

(x + 5/2)² = ±169/4

X + 5/2 = ± 13/2

X = -5/2 ± 13/2

= -5/2 + 13/2

= 4cm

Or

X = -5/2 – 13/2

= -9cm

Since there is no negative dimension, the length of TB is 4cm.

4. XY is a chord of a circle at length 2cm. z is another point on the circle. XY extended meets the length at z at T. if TX = 18cm, find the possible value of TZ

Solution:

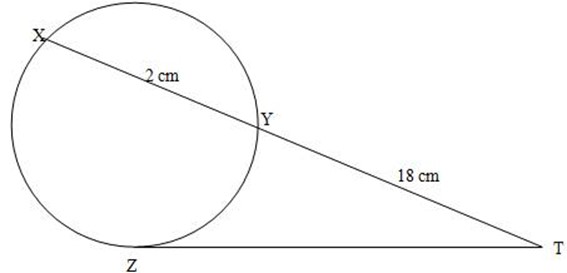
(TY) (TX) = (TZ)²

Since TX = TY + XY

18cm + 2cm= 20cm

From the theorem
(TY) (TX) = (TZ)²

(18cm) (20cm) = (TZ)²

360cm² = (TZ)² square root both sides

(TZ) ² = 360cm²

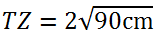
ALTERNATE SEGMENT THEOREM

AT is a tangent to the circle and AB is a chord. The alternate segment theorem state that:-

THEOREM: The angle between the chord and tangent is equal to the angle in the alternate (others)

Segment i.e. < TAB = <ACB

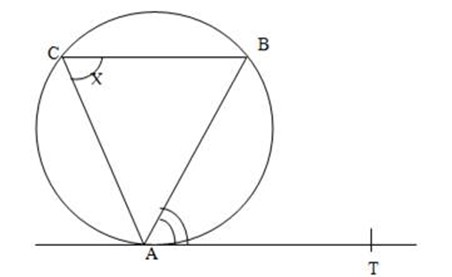
Proof:

 < TAB = <ACB

Aim: Is proving that  <ACB= <BAT

Let ACB = X and Centre of a Circle to be

‘O’ AOB = 2x (< at the centre  is twice the angle at the circumference).

AC,BC, and AB or chords in the Circle and AO = OB

 ∴Δ AOB is isosceles triangle since AO and OB are equal

<OAB=1/2(180º – 2x)

= 90⁰ – x

<BAT+ <OAB =<OAT
<BAT=<OAT – <OAB

                          =90° – (90° – x)

                          = 90⁰-90⁰ +x
=0+x

             ∴<BAT=x
hence proved
∴<ACB=<BAT
=x

QUESTIONS:

1.ABCD is a cyclic quadrilateral TA is the tangent to the Circle at A. if <TAC = 73º, find <ABC

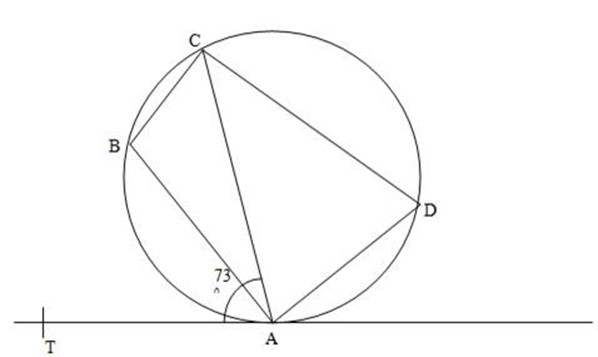
Solution:
TAC = 73⁰

Angle at the same segment equal

TAC = ADC

<ADC + 73⁰  = 180⁰

Take out 73⁰ both sides

<ABC  = 180⁰ – 73⁰

<ABC=107º

2. PQRS is a cyclic quadrilateral. ST is the tangent to the Circle at S. if <QRS = 132º.Find <RST

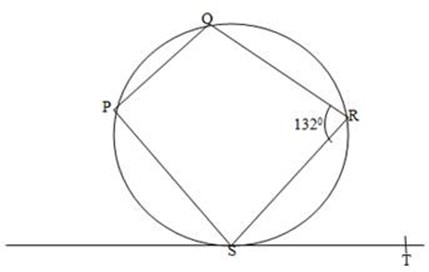
Soln:

<QRS +<RST =180º

132⁰ +132⁰=180º

Take out 132⁰ both sides

<RST =180º-132⁰

=48º

3.  C is the centre of the Circle. If <BAT=39º. find <ACB.

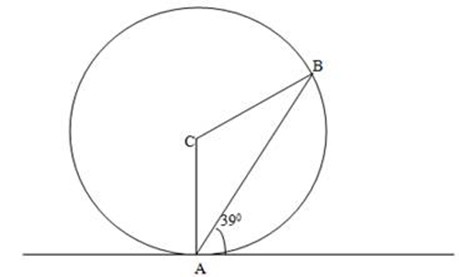
Soln:

Angle at the Centre is twice the angle at circumstances

     <ACB = <BAT

          39º=<BAT

<ACB x 2=< ABC

     < ABC=39º x 2
=78º

4.X is the Centre of the Circle if<CXD =88º, find <TCD

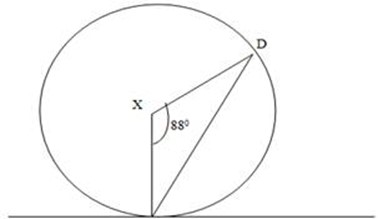
Soln:

 <DXC=<DCT/2

Angle at the Centre  is twice the angle at the circumstances.
∴<TCD=88º/2

              = 44º

THE EARTH AS A SPHERE

SPHERE

Is a set of a point which equidistance (equal distance) from the fixed point called the centre of the Sphere.

-The distance from the centre of the sphere to any point at the circumference of the sphere called Radius at the earth which is approximately as 6370km.

-The surface of the earth is not exactly spherical because it is flattened in its northern and southern pole or we say. The earth is not perfect sphere, as it is slightly flatter at the north and southern pole than at the equator. But for most purpose we assume that it is a sphere