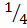A function is a set of ordered pairs which relates two sets such that to each element of one set there is only one element of the second set
Example
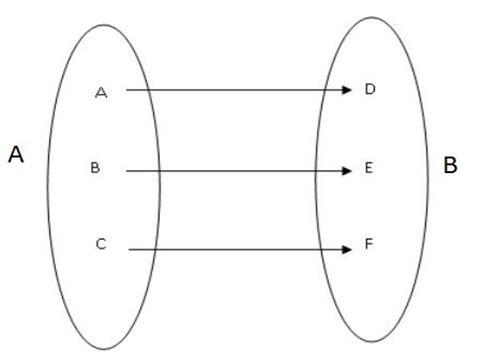
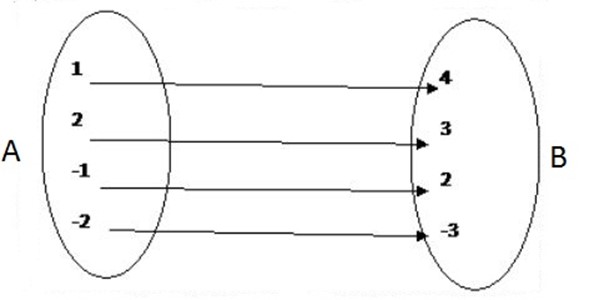
Represent the following set of ordered pairs in a pictorial diagram.
(1,4), (2,3), (-1,2), (-2,-3).
Solution
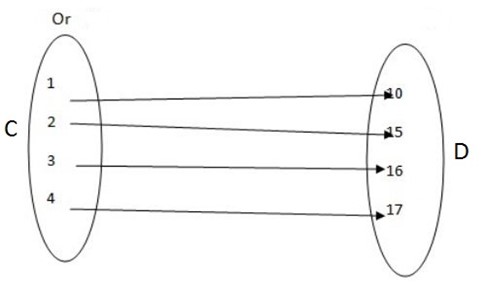
A function whose graph is such that any line drawn parallel to the x – axis at any point cuts it at only one point is one-to-one function.
Examples.
1. Write the expression of a function ‘ double plus one’
Solution
f:x  2x +1
2x +1
b)
2.Given the function G(x) = 4x-1. Find the value of G(-2).
Solution
G(x) = 4x -1
G(-2) = 4(-2) -1
G(-2) = -8 -1
G (-2) = -9
Exercise 2.1
1. Write each of the following function in the form f: x  f(x) use any functions symbol to represent the functions
f(x) use any functions symbol to represent the functions
(a)Divide by 5 and add 2.
(b)Subtract 7 and square
(b)Cube and then double
Solution
(a) F:x  f(x)
f(x)
F:x 
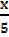 + 2
+ 2
(b) F: x  (x-7)2
(x-7)2
(c) F:x  x3+2x
x3+2x
2. Find the value of the function for each given value of x.
(a) f(x)= 2x+3; when
(i) x=1
(ii) x= -2
(iii) x =a
Solution
(a) (i) when x=1
f(x)= 2x+3
f(1)= 2(1)+3
f(1)= 2+3
∴ f(1)= 5.
(ii)when x= -2.
f(x) = 2(-2) +3
f(-2) = -4+3
∴f(-2) = -1
(iii) when x=a
f(x) = 2(a) +3
f(a) =2a+3
∴f(a) = 2a+3
(b) C(x) = x3; when
(i) x=1
(ii) x = -1
(iii)x= 0
(iv)x=b
Solution
(i) C(x) =x3
C (1) =13
C (1) =1
C (1) =1
(ii)C(x) =x3
C (-1) = (-1)3
C (-1) = -1
(iii)C(x) =x3
C (0) =03
C (0) =0
(iv)C(x) =x3
C(b) = b3
(c) K(x) = 3-x; when
(i) x= -1
(ii)x=7
Solution
(i) K(x) = 3-x
K (-1) = 3- (-1)
K (-1) = 4
(ii) k(x)=3 – x
k(7) = 3-7
k(7) = -4
DOMAIN AND RANGE OF FUNCTIONS
Example 1.
1. Find the domain and range of f(x) =2x+1
let f(x) = y
y=2x+1
Solution
Domain = {x: x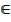 R}
R}
Range – make x the subject
y=2x+1
y-1=2x
(y-1)/2 =x
∴x=(y-1)/2
Range={y: y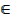 R}
R}
b Example 2
If y =4x+7 and its domain ={x : -10 < x< 10} find the range.
Solution
Domain = {x: -10 < x< 10}
Range ={y : -33 < y < 47}
y = 4x + 7
Table of values

c Example 3.
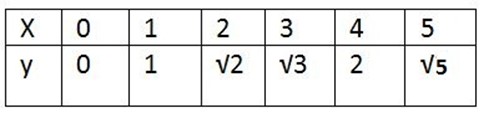
Y= √x and domain is -5 < x < 5, Find its range.
Solution
Domain = {x: -5 < x < 5}
Range =y
Table of value of x = √(y)
(y)2= (√x)2
y2= x
x= y2
√5= √y2
y = √5
Range = {y: o < y < √5}
d Example 4.
Given F(x) =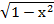 find the domain and range.
find the domain and range.
Solution
Let f(x)=y
Domain of y= 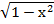
For real values of y: 1-x2
> 0
-x2
> 0-1
-x2
> -1
x2
< 1
√x2< √1
X <√1
X <1
∴Domain {x : X <1 }
let F(x) = y
y=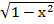
To get the range, make x the subject
y2 = (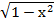 )2
)2
y2= 1-x2
X2=1-y2
Therefore 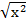 =
= 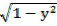
X=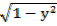
For real value of x:
1- y2 > 0
y2 < 1
y < √1
y < 1
...Range ={y : y <1}
LINEAR FUNCTIONS
Is the function with form f(x) = mx + c.
Where:
f(x)= y
m and c are real numbers
m is called gradient[ slope].
c is called y – intercept.
Example
1. Find the linear function f(x) given the slope of -2 and f( -1)=3
Solution
Given:
m(slope)=-2
x=-1
f(-1)=3
from;
f(x) =mx +c
f(-1) =( -2x-1)+c
3 =2+c
3-2 =c
c=1
∴f(x) = -2x+1
Example 2.
Find the linear function f(x) when m=3 and it passes through the points (2, 1)
Solution
f(x) =mx +c
f(2) = 3(2)+ c
1= 6+c
1-6 =c
-5 = c
c= -5
f(x) = 3x + -5
∴ f(x) =3x-5
Example 3
Find the linear function f (x) which passes through the points (-1, 1) and (0, 2 )
Solution
Slope = 
=1
m = 1
f(x) = mx +c
f(-1) = 1x(-1) +c
1 =-1+c
c=2
f(x) = 1x +2
∴f(x) = x +2.
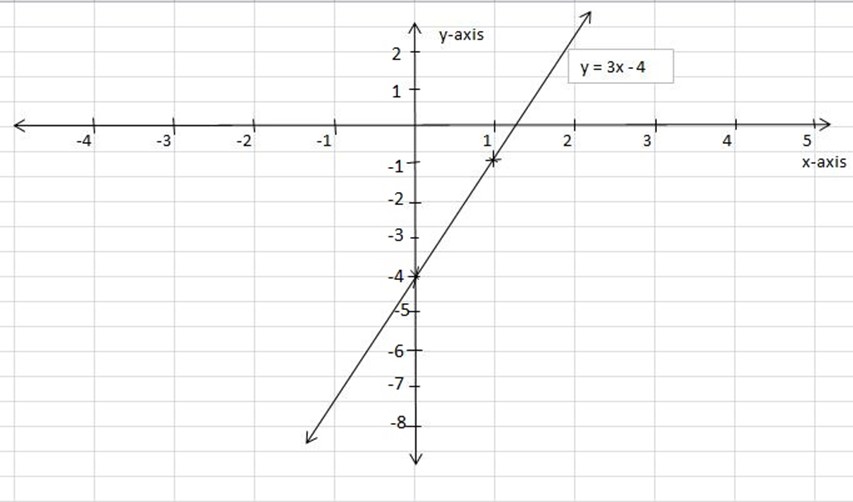
4.Draw the graph of h(x) = 3x-4
Table of values of function
| X | -1 | 0 | 1 |
| h(x) | -7 | -4 | -1 |
edu.uptymez.com
Exercise
In problems 1 to 3 find the equation of a linear function f(x) which satisfies the given properties. In each case, m dissolves the gradient.
1). m =-3, f(1) = 3
2). m=2, f(0) =5
3). f(1) =2, f(-1) =3
4. Givenm= -4 , f(3) = -4 Find f(x)
In the problem 5 to 9 draw the graphs of each of the given functions without using the table of values
5) f(x)= 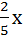 +
+
6) f(x) =4
Solution
1. f(x) = mx + c
f(x) = -3(1)+c
f(x) =-3 +c
3= -3 +c
3+3 =c
6=c
C=6
f(x) = -3x +6
2. f(x) =mx +c
f(0) = (2 x 0)+c
5= 0+c
c=5
f(x) =2x+5
3)
3.f(1) =2, f(-1) =3 Alternatively
m = 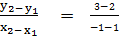 f(-1) = m(-1) + c
f(-1) = m(-1) + c
M= 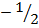 3= -m + c…………………..(i)
3= -m + c…………………..(i)
f(1)=2 f(1) = m(1) + c
f(x)= mx +c 2= m + c(ii)
f(1)= –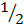 x 1+c Solve (i) and (ii) Simultaneously
x 1+c Solve (i) and (ii) Simultaneously
f(1) = –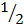 +c -m + c = 3
+c -m + c = 3
2=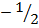 +c + m + c = 2
+c + m + c = 2
2+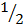 = c C=5/2
= c C=5/2
C=2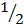 put c in (i)
put c in (i)
f(x) =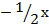 + 2
+ 2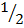 3 = -m + 5/2
3 = -m + 5/2
m = 5/2 – 3
m= -1/2
...f(x) =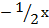 + 2
+ 2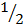
4.
f(x)= mx + c
f(x) = -4(3)+c
-4 =-12+c
-4+12= c
8=c
C=8
f(x) = -4x+8
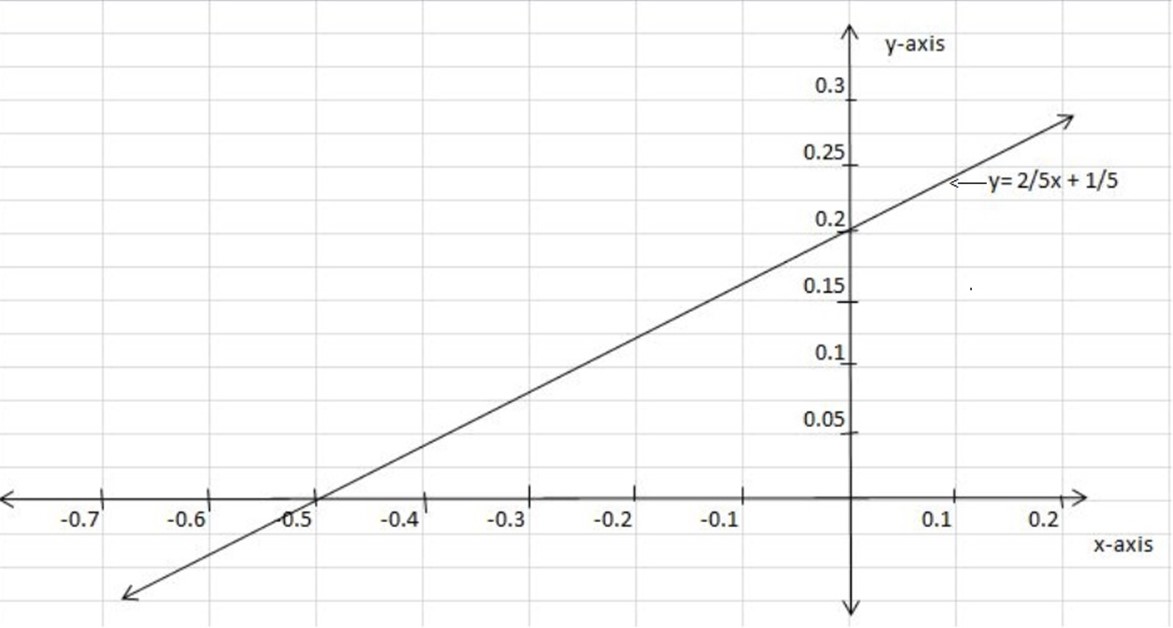
5. f(x)= 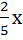 +
+
y- intercept, x=0
f(0)= 2/5[0] +1/5
f(0)= 0+1/5
y=1/5
{0,0.2}
x- intercept, y=0
0=2/5[x] +1/5
x intercept = – ½ ( -1/2, 0)
y intercept = 1/5 ( 0,0.2)
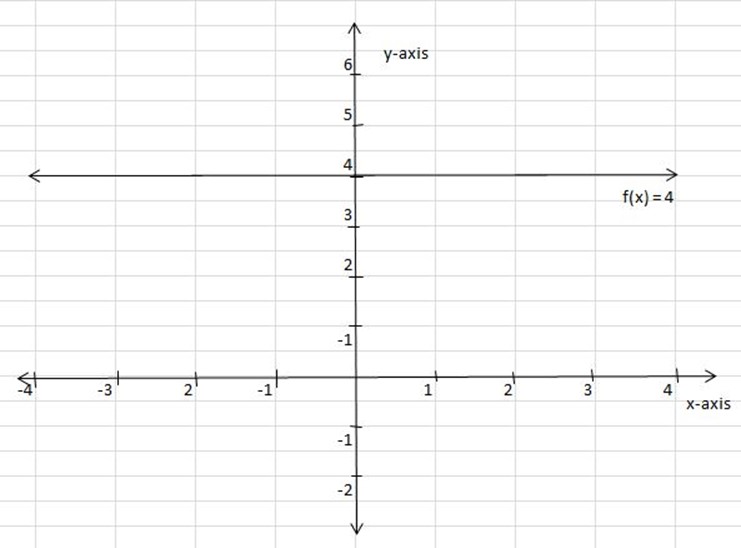
6. f(x) =4
From f(x) = y
y = 4
QUADRATIC FUNCTIONS
A quadratic function is any function of the form;
f(x)=ax2+bx+c
Where a ≠ 0
a ,b and c are real numbers.
When a = 1, b=0, and c= 0
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
edu.uptymez.com
The shape of the graph of f(x)=ax2+bx+c is a parabola
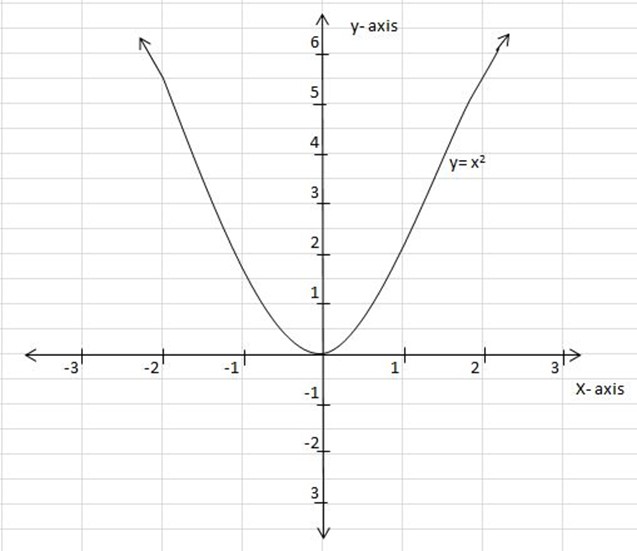
•The line that divides the curve into two equal parts is called a line of symmetry [axis of symmetry]
•Point (0,0) in f(x)=x2 called the turning point (vertex).
If “a” is positive the turning point is called minimum point (least value).
If “a” is negative the turning point is called maximum point.
PROPERTIES OF QUADRATIC FUNCTIONS
Think of f(x)= ax2+bx+c
y=a(x2+bx/a)+c
y= a( x2+bx/a+b2/4a2)+ c-b2/4a2
=a(x + 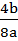 ) 2 +
) 2 +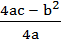
x> 0 then
a(x+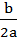 )2
)2
> 0
y = 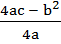
This is when x = –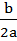
The turning point of the quadratic function is 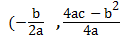 )
)
Example
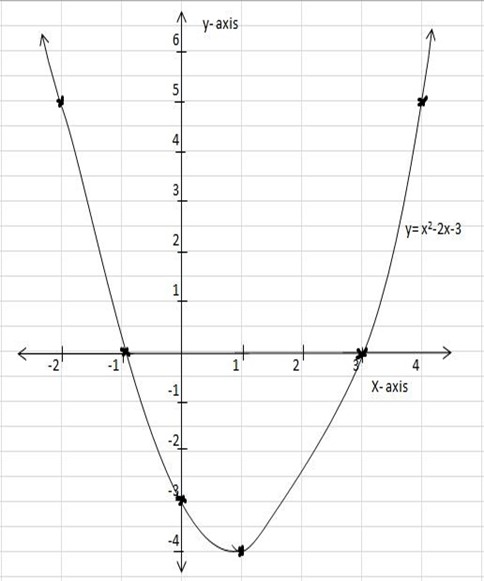
Find the minimum or maximum point and line of symmetry f(x) = x2 – 2x-3. Draw the graph of f(x)
Solution:
Turning point =  )
)
= ( – 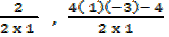 )
)
Maximum point = (1, -4)
Line of symmetry is x=1
| x | -5 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| f(x) | 15 | 5 | 0 | -3 | -4 | -3 | 0 | 5 |
edu.uptymez.com
Exercise
1. Draw the graph of the function y=x2-6x+5 find the least value of this function and the corresponding value of x
Solution
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 32 | 21 | 12 | 5 | 0 | -3 | -4 | -3 | 0 |
edu.uptymez.com
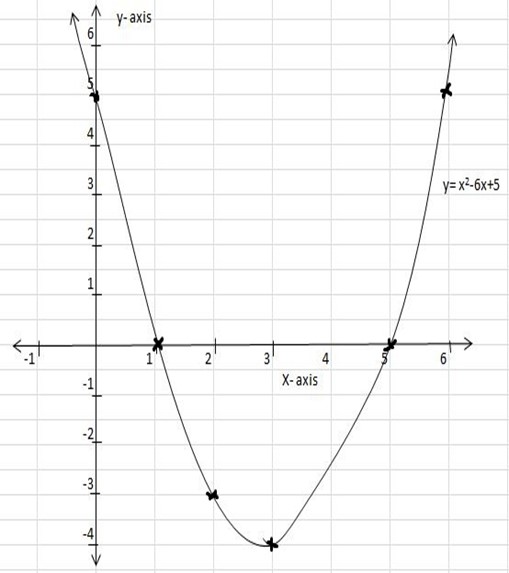
Least value.
y= – 4 where x=3
2. Draw the graph of the function y =x2-4x+2 find the maximum function and the corresponding value of x use the curve to solve the following equations
a) X2-4x-2 = 0
b) X2-4x-2 = 3
b)
Solution
Table of values of y= x2-4x+2
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 23 | 14 | 7 | 2 | -1 | 2 | -1 | 2 | 7 | 14 |
edu.uptymez.com
Find the maximum value of the function.;
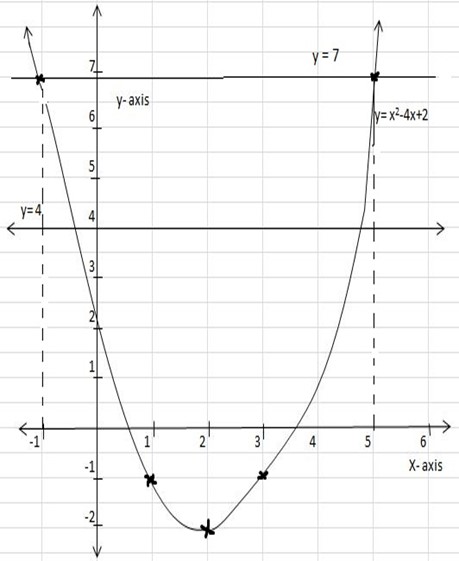
Maximum value
=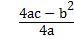
Y= ( 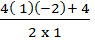 ) = – 2
) = – 2
Find the maximum value of the function;
Maximum value= 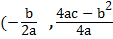 )
)
Maximum value= 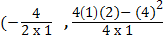 )
)
Maximum value
[2, -2]
The maximum value is = (-2,-2)
a) x2-4x-2 = 0
add 4 both sides
x2-4x + 2 = 4
but x2-4x+2 = y
... y = 4
Draw a line y = 4 to the graph above. The solution from the graph is
x1 = -1/2 , x2 = 9/2
(x1,x2) = (-1/2,9/2 )
(b) x2-4x – 2 = 3
add 4 both sides
x2-4x – 2 +4 = 3+ 4
x2-4x + 2 = 7
but x2-4x+2 = y
... y = 7
Draw a line y = 7 to the graph above. The solution from the graph is
x1 = -1 , x2 = 5
(x1,x2) = (-1,5 )
3. In the problem 3 to 5 write the function in the form f(x)= a( x + b)2 +c where a, b, c are constants
f(x) =5-x-9x2
Solution
f(x) = -9x2 – x + 5
= -9( x2 –  ) + 5
) + 5
= -9( x2 – 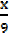 +
+ 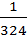 ) + 5 +
) + 5 + 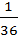
= -9(x – 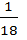 )2 +
)2 + 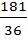
4. In the following functions find:
a) The maximum value
b) The axis of the symmetry
f(x)= x2– 8x+18
Solution
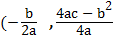 ) =
) = 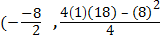 )
)
( 4, 2)
Maximum value =2 where the axis of symmetry x=4.
5. f(x) = 2x2+3x+1
Solution
Maximum value 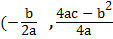 )
)
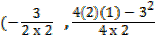 )
)
The turning point of the graph is 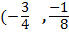 )
)
The minimum value of the graph is y = – 
axis of symmetry = 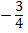
POLYNOMIAL FUNCTIONS
The polynomial functions are the functions of the form, ” P(x) =an xn + a n-1 xn-1 + an-2 xn-2 + . . . + a1 x1+a0 x0 “. Where n is non negative integer and an, an-1, an-2 . . . a0 are real numbers. The degree of a polynomial function is the highest power of that polynomial function.
Example
a) f(x) =5x4 -7x3 +8x2– 2x+3 is a degree of 4
b) H(x)=6x-8x2+9x9-6 is a degree of 9
c) G(x) =16x-7 is a degree of 1
d) M(x) =6 degree is 0 =6x0
GRAPHS OF POLYNOMIAL FUNCTIONS
EXAMPLE
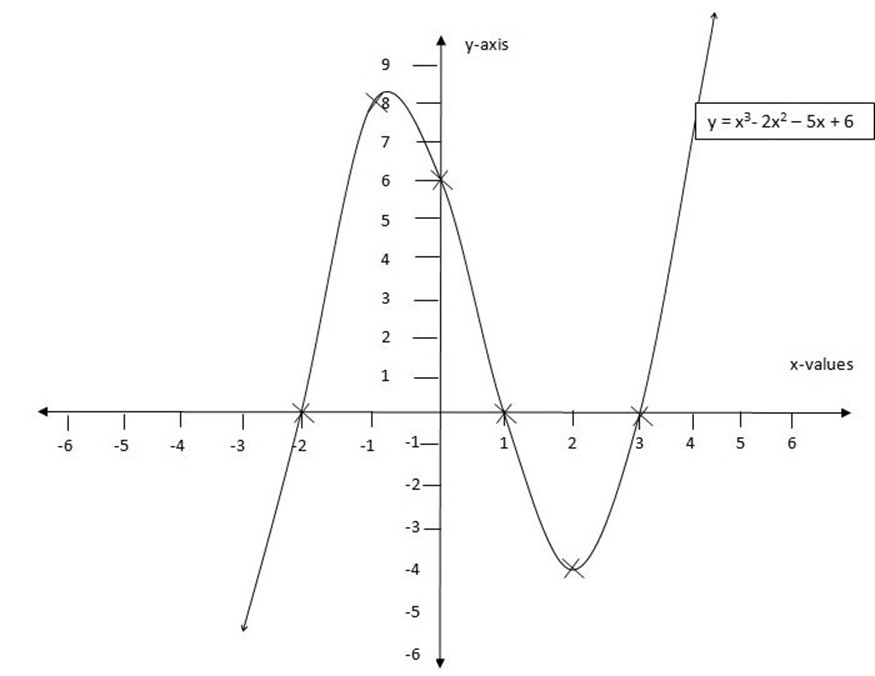
Draw the graph of f(x) = x3-2x2-5x+6
Solution
Table of values
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
| F[x] | -24 | 0 | 8 | 6 | 0 | -4 | 0 | 18 |
edu.uptymez.com
STEP FUNCTIONS
EXAMPLE
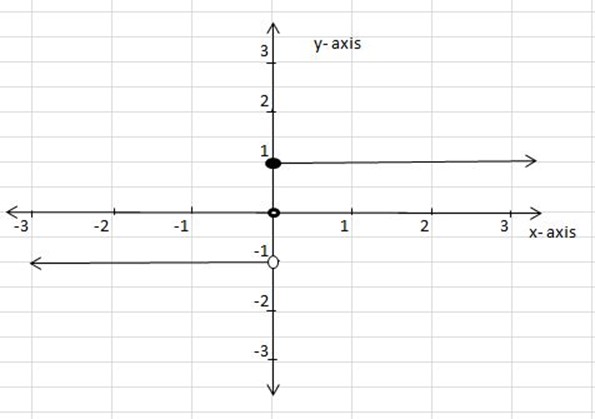
1. If f is a function such that;
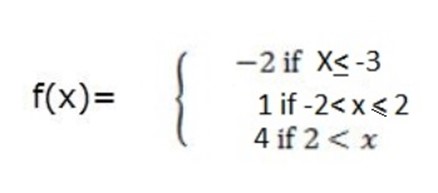
Draw the graph and find its domain and range.
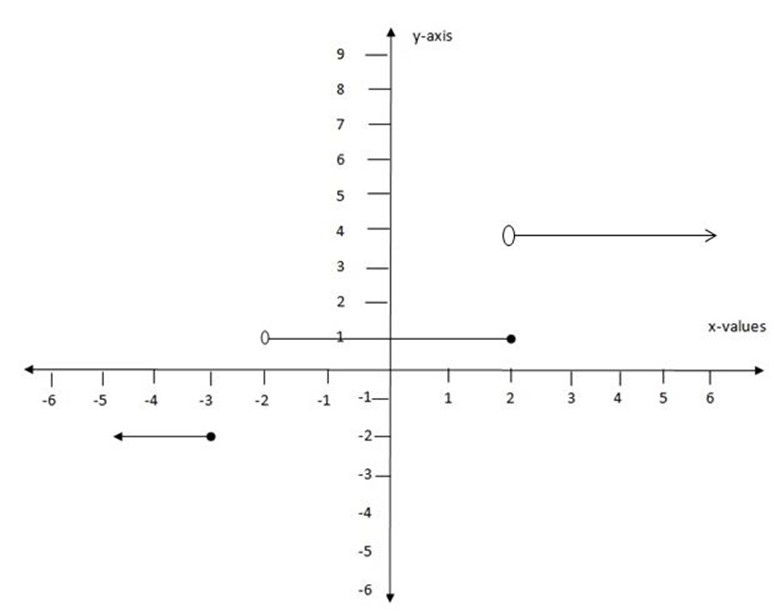
Domain = {x: x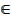 R, except -3< x < -2}
R, except -3< x < -2}
Range = {1,4, -2}
2. The function is defined by

a)
Sketch the graph of f(x) use the graph to determine the range and the domain. Find the value of f(-6) , f(0). State if it is a one to one function
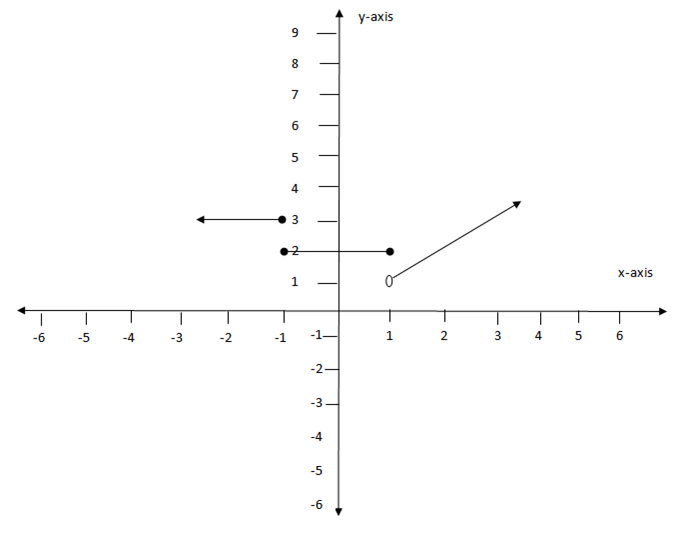
Domain
= {x : X R}
R}
Range
{ y:y >1}
f(-6) = -2
f(0)= 2
It is not a one to one function.
EXERCISE
1. Draw the graph of the following defined as indicated
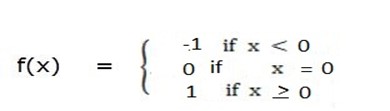
Solution:
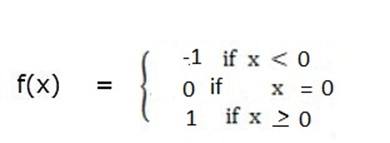
Solution
2. Given that f(x) = 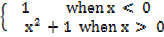
a) On the same set of axes sketch the graphs of f(x )and the inverse of f(x), From your graphs in [a] above determine;
(a)The domain and range of f(x)
(b)The domain and range if the inverse of f(x)
(c)Find f(- 5)and f(5)
(d)Is f (x)a one to one?
(e)Is the inverse of f(x) a function?

(a) Domain of f(x ) = { x: x 
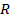 }
}
(b) •Range of f(x) = { y : y 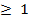 }
}
•Domain of f-1(x ) = { x : x 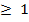 }
}
(c) Range of f-1(x ) = { y: x 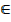
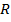 }
}
(d) f(-5) = 1 and f(5) = 6
(e)Yes the inverse of f(x) is a function and f(x) is one-to-one function
ABSOLUTE VALUE FUNCTIONS
The absolute value function is defined by f(x) 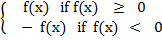
Example
1. Draw the graph of f(x) = | x |
Solution
Table of values f(x) = | x |
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 3 | 2 | 1 | 0 | 1 | 2 | 3 |
edu.uptymez.com
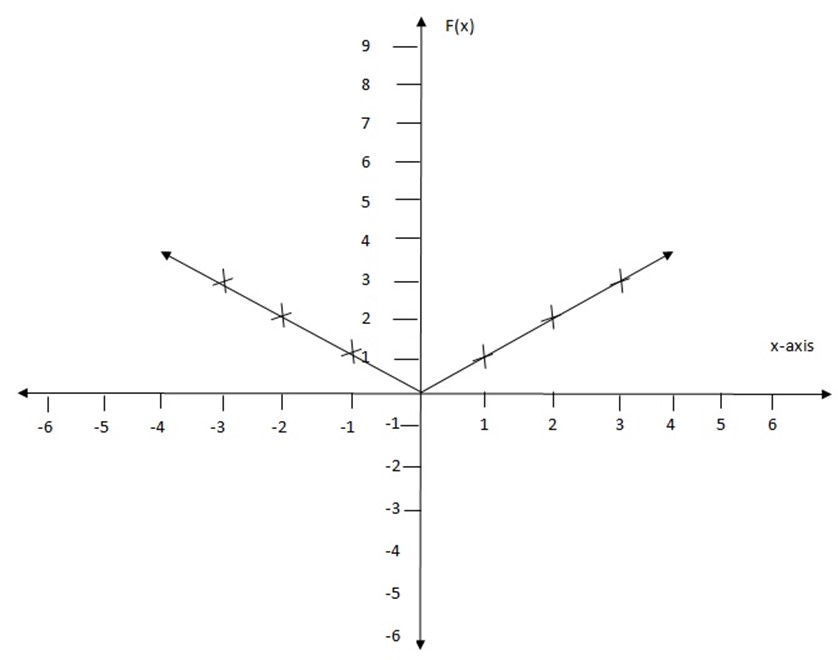
THE INVERSE OF A FUNCTION
Given a functon y= f(x), the inverse of f(x) is denoted as f-1(x). The inverse of a function can be obtained by interchanging y with x (interchanging variables) and then make y the subject of the formula.
Example
1. Find the inverse of f(x) = 2x+3
Solution
Y= 2x+3
X=2y+3
2y=x-3
Y =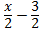
∴ f-1(x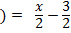
EXPONENTIAL FUNCTIONS
An exponential function is the function of the form f(x) = nx where n is called base and x is called exponent.
Example
1. Draw the graph of f(x)=2x
Solution :
Table of values
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 1/8 | 1/4 | ½ | 1 | 2 | 4 | 8 |
edu.uptymez.com
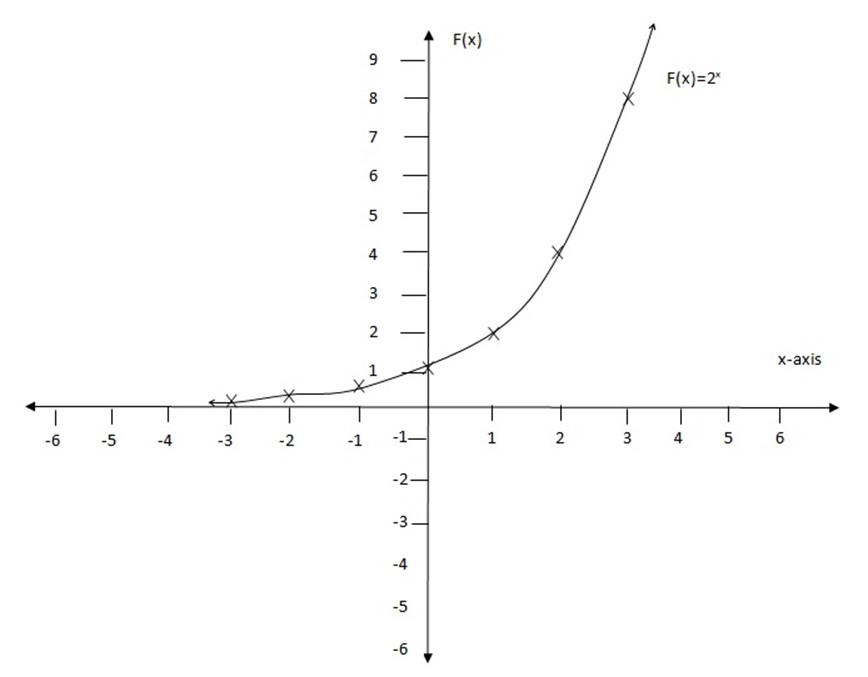
2. Draw the graph of f (x)=2-x
Solution:
Table of values
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(X) | 8 | 4 | 2 | 1 | 1/2 | ¼ | 1/8 |
edu.uptymez.com
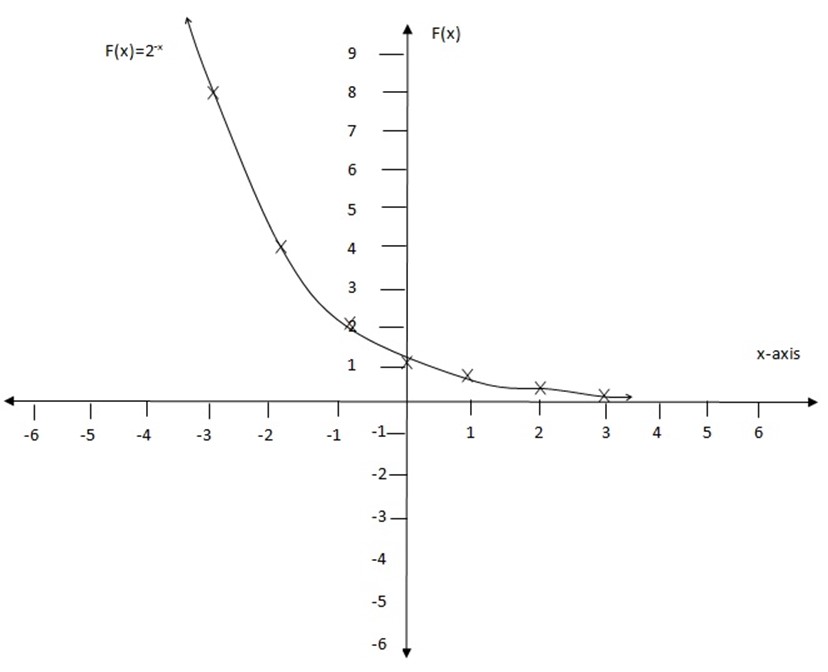
Properties of exponential function
- When x increases without bound, the function values increase without bound
- When x decreases, the function values decreases toward zero
- The graph of any exponential function passes through the point (0,1).
- The domain of the exponential function consists of all real numbers whereas the range consist of all positive values.
edu.uptymez.com
LOGARITHMIC FUNCTION
Logarithmic function is any function of the form f(x)= 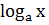 read as function of logarithm x under base a or f(x) is the logarithm x base a
read as function of logarithm x under base a or f(x) is the logarithm x base a
Example
Draw the graph of f(x)=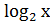
Solution
Table of values
| x | 1/8 | ¼ | 1/2 | 1 | 2 | 4 | 8 |
| f(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
edu.uptymez.com
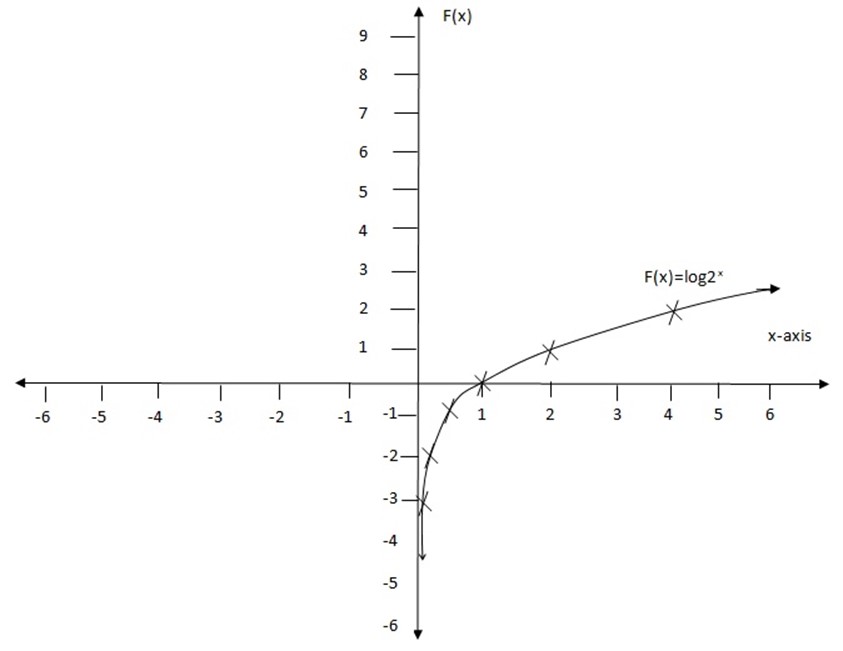
THE INVERSE OF EXPONENTIAL AND LOGARITHMIC FUNCTION
The inverse of the exponential function is the relation of logarithmic in the line y=x
EXAMPLE
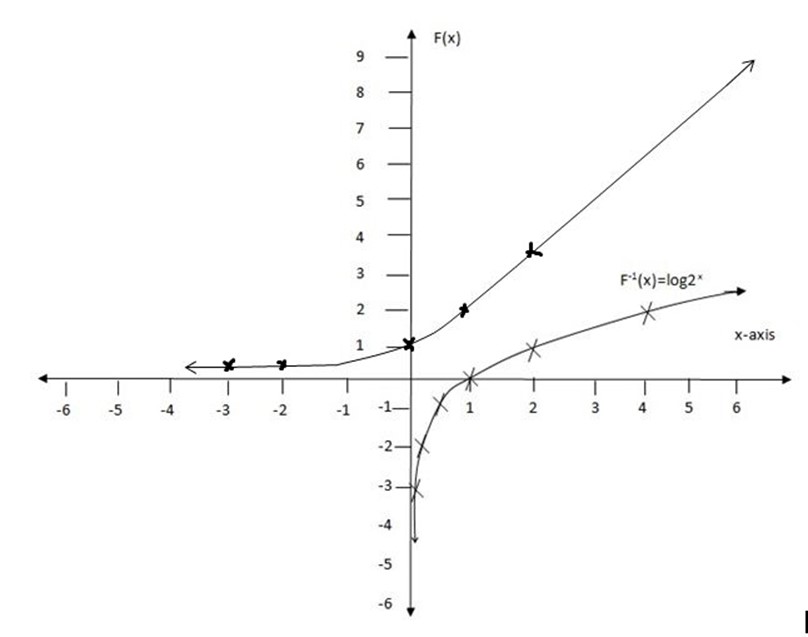
1. Draw the graph of the inverse of f(x) = 2x and f(x)=  under the same graph.
under the same graph.
Solution
(i) y= 2x
Apply log on both sides
log x=log 2y
log x =y log 2
y = log (x- 2)
f-1(x) = log (x- 2)
(ii) f(x)=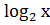
y= 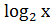
x= 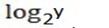
y= 2x
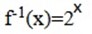
Table of values
| X | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 |
| f(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
edu.uptymez.com
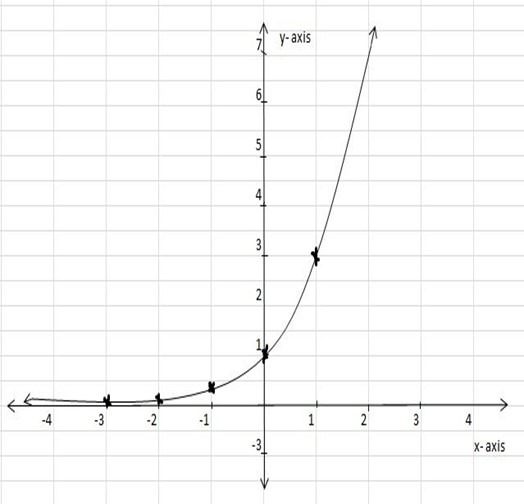
2. Draw the graph of the function f(x)=3x
Table of values
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(X) | 1/27 | 1/9 | 1/3 | 1 | 3 | 9 | 27 |
edu.uptymez.com
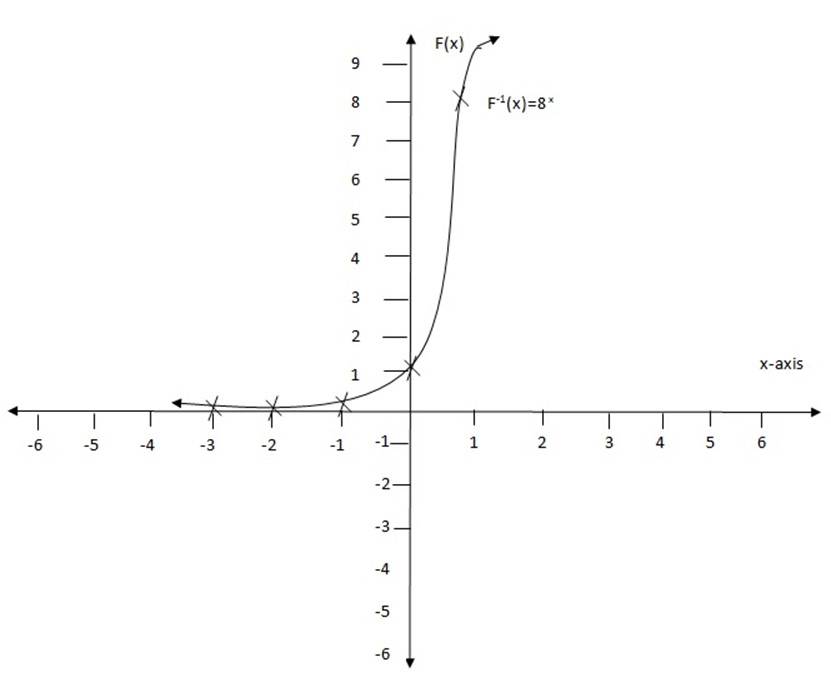
3. Draw the graph of the function f(X)=8x
Solution
Table of values
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(X) | 1/512 | 1/64 | 1/8 | 1 | 8 | 64 | 512 |
edu.uptymez.com
Exercise
1. Find the graph of y =2x and given that ¾ =2-0.42 draw the graph of f(x)= (3/4)x
Table of values if f(x) =(3/4)x
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 2x | 1/8 | 1/4 | ½ | 1 | 2 | 4 | 8 |
| -0.42x | 1.26 | 0.84 | 0.42 | 0 | -0.42 | -0.84 | 1.26 |
| 2-0.42x | 64/27 | 16/9 | 4/3 | 1 | 3/4 | 9/16 | 27/64 |
edu.uptymez.com
Copy and complete the following table and hence draw the graph of f(x)=(1/4)x
| X | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 2x | -6 | -4 | -2 | 0 | 2 | 4 | 6 |
| -2x | 6 | 4 | 2 | 0 | -2 | -4 | -6 |
| 2-2x | 64 | 16 | 4 | 0 | 1/4 | 1/16 | 1/64 |
| [1/4]x | 64 | 16 | 4 | 0 | 1/4 | 2/4 | ¾ |
edu.uptymez.com
OPERATION OF POLYNOMIAL FUNCTION
ADDITIONAL AND SUBTRACTION
The sum of two polynomials is found by adding the coefficients of terms of the same degree or like terms, and subtraction can be found by subtracting the coefficient of like terms.
EXAMPLE
If p(x) = 4x2– 3x+7, Q(x) =3x+2 and r(x)= 5x3-7x2+9
Solution
Sum =p(x)+q(x)+r(x)
(4x2-3x+7)+(3x+2)+(5x3-7x2+9)
4x2-3x+7+3x+2+5x3-7+9
4x2+5x2+7x3+3x+7+2+9
5x3-3x2+18
Alternatively the sum can be obtained by arranging them vertically
4x2-3x+7
0x2+3x+2
5x3-7x2+0+9
5x3-3x2+0+18
P(x)+q(x)+r(x)=5x3-3x2+18
Subtract -5x2+9+5 from 3x2+7x-2
Solution
(3x2+7x-2)-(-5x2+9x+5)
3x2+7x-2+5x2-9x-5
3x2+5x2+7x-9x-2-5
8x2-2x-7 answer
MULTIPLICATION
The polynomial R(x) and S(x) can be multiplied by forming all the product of terms from R(x) and terms from S(x) and then summing all the products by collecting the like terms.
The product can be denoted by RS(X)
example
If p(x)=2x2-x+3 and q(x)=3x3-x find the product p(x)q(x)
Solution
P(x) q(x)= (2x2-x+3) (3x3-x)
6x5-2x3-3x4+x2+9x3-3x
6x5-3x4+7x3+x2-3x
DIVISION
The method used in dividing one polynomial by another polynomial of equal or lower degree is the same to the one used for the long division of number
Example:
1. Given p[x] =x3-3x2+4x+2 and q[x]=x-1 find 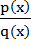
Solution
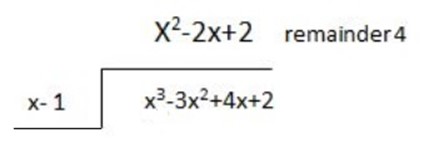
x3-x2
0-2x2+4x
-2x2+2x
0+2x+2
2x-2
0+4
Therefore
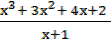 = x2 – 2x + 2 +
= x2 – 2x + 2 + 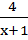
This means
X3– 3x2+4x+2 is dividend x-1 is divisor
X2-2x+2 is the quotient and 4 is the remainder
Then
X3-3x2+4x+2 = (x2-2x+2) (x-1) + 4
Divided quotient x divisor + remainder
2. Divide p(x) = x3-8 by q(x) = x-2
Solution:

-x3 -2x2
2x2-8
-2x2-4x
4x-8
4x-8
– –
In the example [2] above there is a remainder i.e. the remainder is zero so dividing one function by another function is one of the way of finding the factors of the polynomial thus if we divide p(x) by q(x) is one of the factors of p(x) other factors can be obtained by fractionazing the quotient q(x).
3. Given p(x) = x3-7x+6 and q(x) = x+3 determine whether or not d(x) is one of the factors of p(x) and hence find the factors if p(x)
Solution
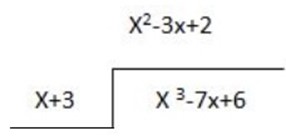
X3+3x2
-3x2-7x
-3x2-9x
2x+6
-2x+6
– –
Since the remainder is zero d(x) =x+3 is one of the factors of p(x)
To factorize
X2-3x+2
(x2-x) – (2x+2)
x(x-1)-2(x-1)
(x-2) (x-1)
Therefore other factors are (x-2) and (x-1)
THE REMAINDER THEOREM
The remainder theorem is the method of finding the remainder without using long division
Example
1. If p(x) = (x-2) and q(x)+8. Dividend divisor quotient remainder, Then by taking x-2=0 we find
x-2= 0
x=2
subtracting x=2 in p(x)
p(2) =2-2 q(x) +r
p(2)= 0 x q(x)+r
p(2)= 0+r
p(2) =r
So the remainder r is the value of the polynomial p(x) when x=2
2. Give p(x) = x3-3x2+6x+5 is divided by d(x) = x-2 find the remainder using the remainder theorem
Solution
Let d(x)=0
x-2=0
X-2+2 =0+2
X=2
Subtracting x=2 in p(x)
P(2)= 23-3[2]2+6[2]+5
P(2)=8-12+12+5
P(2)=8+5
P(2)=13
The remainder is 13
3. The remainder theorem states that if the polynomial p[x] is divided by [x-a] then the remainder ‘r’ is given by p[a]
P(x) =(x-a) q(x)+r hence
P(a) =(a-a) q(x)+r
P(a)=o(q(x))+r
P(a)=0+r
P(a)=r
More Examples
1. By using the remainder theorem, Find the remainder when p[x] =4x2-6x+5 is divided by d[x] =2x-1
Solution
d (x)=0
2x-1=0
2x-1+1=0+1
X = 
Substituting
X=  in p(x)
in p(x)
P( ) =4 x
) =4 x 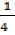 -6(
-6( )+5
)+5
P( )=1 – 6 x
)=1 – 6 x  +5
+5
P( )=1 -3+5
)=1 -3+5
P( )= 3
)= 3
The remainder is 3
2. P(x)= 3x2-5x+5 is divided by d(x) =x+4
Solution
Let d(x)=0
X+4=0
X+4=0-4
X=-4
Subtracting x=-4 in p(x)
P(-4)=3(-4)2-=5(-4)+5
P(-4)=48+20+5
P(-4)=68+5
P(-4)= 73
The remainder is 73
3. P(x)= x3+2x2-x+4 is divided by d(x) = x+3
Solution
Let d(x)=0
X+3=0-3
X=-3
Substituting x=-3 in p(x)
P(-3)= -33+2(-3)2-(-3)+4
P(-3)=-27+18+3+4
P(-3)=-27+21+4
P(-3)=-27+25
P(-3)=-2
The remainder is -2
4. Find the value of ‘a’ if x3-3x2+ax+5 has the remainder of 17 when divided by x-3
Solution
By using remainder theorem
Let x-3 =0
x-3=0+3
x=3
Substituting x=3 we have
x3-3x2+ax+5=17
(3)3-3(3)2+a(3)+5=17
27-27+3a+5=17
3a+5=17-5
3a=12
a=4
5. If ax2+3x-5 has a remainder -3 when divided by x-2. Find the value of a.
Solution
By using the remainder theorem
Let x-2=0
x-2=0+2
x=2
subtracting x=2 we have
a(2)2+3(2)-5 =-3
4a+6-5= -3
4a+1= -3
4a= -4
a = -1
Exercise
1. Divide p(x) by d(x) in the following
P(x)=2x2+3x+7 d(x)=x2+4
Solution


Use remainder theorem to find the remainder when;
1. P(x)=x3-2x2+5x-4 is divide by d(x)=x-2
Solution
Let d[x]=0
x-2 + 2=0+2
x=2
substituting x=2 in p(x)
p(2)=23-2[2]2+5[2]-4
p(2)=8-8+10-4
p(2)=10-4
p(2)=10-4
p(2)=10-4
Therefore the remainder is 6
2. p(x)= 2x4+ x3+x- 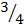 is divided by d(x)=x+2
is divided by d(x)=x+2
solution
let d(x)=0
x+2 – 2 = 0-2
x = -2
Substituting x = – 2 in p(x)
p(-2)=2(-2)4+(-2)3+(-2)( –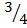 )
)
p(-2)= 2(16)+(-8)-2( –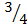 )
)
p(-2)=32-8-2 ( –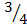 )
)
p(-2)=24-2( –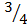 )
)
p(-2)=21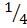
Therefore the remainder is 21