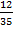Defn:
Probability is a branch of mathematics which deals with and shows how to measure these uncertainties of events in every day life. It provides a quantitative occurrences and situations. In other words. It is a measure of chances.
Probability set and Event
Suppose that an experiment of tossing a fair coin is done once. The outcomes expected from this experiment are that the coin will show up a head (H) or a tail (T). The results of the experiment are called outcome. All expected outcome from the possibility set or sample space, which is denoted by S.A
Specified outcome is called an even and is denoted by E. For example in this experiment the outcome that a head shows up is an event and it is a subset of the possibility set. Thus S ={H,T} and E ={H}
An event may not occur. For example, If the event is that a head occurs in tossing a coin once but a tail occurs instead. Then the event did not occur and is denoted by E‘: E’. Is the complement of E. In this experiment the space S = {H,T}. If the outcome is a head showing up, the E = {H}. So the event that is a head does not show up is E‘ = {T}
Formula of Probability of Event
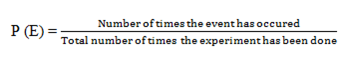
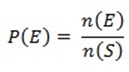
Keys
Outcomes;
Sample space (S)
Event (E)
The probability of an event is the number P where 0 ≤ P ≤ 1 that measures the likelihood that the event will occur when the experiment is performed.
Example of probability experiment
1. Tossing a coin with outcomes; head or tail.
2. Throwing a die with outcomes 1, 2, 3,4,5,6.
3. Aiming at a target with outcomes of Success or failure
4. Testing an electrical component, outcomes defective or non- defective.
Event.
An event A is a subset of the sample space ( A⊆S) or event is a specific outcome.
Example.
1. Three coins are tossed once each.
S= 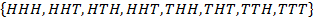
E = 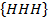 is an event where exactly 3 heads appear.
is an event where exactly 3 heads appear.
E = 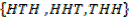 is an event where exactly one tail shows up.
is an event where exactly one tail shows up.
2. A die is tossed once and the results are recorded.
a. The sample space
b. The event that an even number occurs.
c. The event that an even number does not occur.
Answer
a. S = 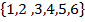
b. E = 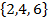
c. E = 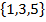
3. Give the possibility set of the experiment of selecting even number less than 20.
S = 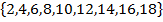
4. Give the possibility set of not selecting an even number from a set of numbers less than 9.
S = 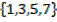
DISCRETE RANDOM VARIABLE.
Is the one that assumes only a countable number if values .
If “S” has “n” number of elements and if by symmetry each of these elements has the same probability to occur , then this probability is in 1/n . if A has “m” elements,
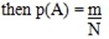
Example.
1.If we toss two fair coins, let A be the event that at least one head shows up . find P (A).
Solution:
S = 
n(s) =4
E(n) = 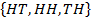
At least greater or equal
nE(A) = 3
P(A) = 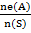
= 3/4 = 0.75
2.find the probability that an odd number appears in a single toss of a fair die.
Solution:
S = 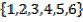
n(S) = 6
E(n) = 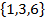
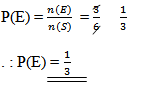
Some properties of probability.
1. 0≤P(A)≤1
2. P(S)=1
3. P(Q)=0
4. P(A) = 1-P(A)
Exercise 1.1
1. If the probability that it rains at Dar-ES-Salaam on April 1st in any year is 0.4, what is the probability that it will not rain at Dar-Es-Salaam on April first next year?
Solution:
P(A) = 1- P(A)
= 1- o.4
= 0.6
2. A box contains 6 volley balls and 8 footballs of the same size. If one ball is picked at random, what is the probability that it will be a football?
Solution:
n(S)= 14
n(f)= 8
p(f) = 8/14
p(f) = 4/7
COMBINED EVENT AND TREE DIAGRAM
Example
In a family of three children, write down an event where all the children are boys.
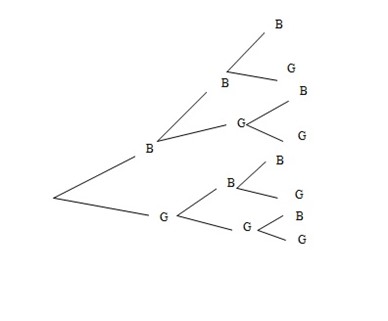
S= 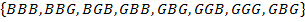
E= 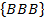
E= 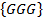
P(GGG) = 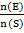
= 1/8
The probability at least two are boys;
E = 
n(E) = 4
P(E) = 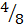
= 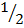
Exercise 1.2
1. 1. If a two digit numeral is written choosing the 10 digit from the set (1,2,3,4) and unit’s digit from (5,6) . find the probability that a number greater than 20 will appear.
2.A pair of dice is tossed . find the probability that the sum of the two numbers obtained is;
a. At least 8
b. At most 10
3.Maria has two blouses, one is green and the other is yellow. She also has a blue , white and black shirt . what is the probability that she will put on a yellow blouse and a blue shirt ?
Answers
Solution1.

S= 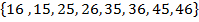
E = 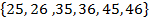
P(E) = 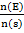
= 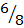
= 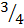
Solution 2.
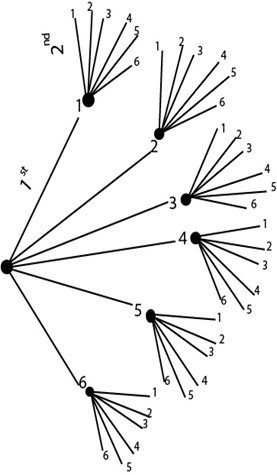
S= 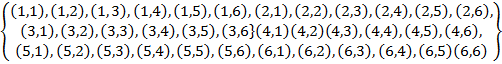
(a).
n(s) = 36
n(E) = 15
P(E) = 
(b).
n(E) = 33
p(E) = 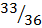 =
= 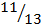
Solution 3.
|
|
Shirts |
|||
|
blouse |
|
blue |
White |
Black |
|
Green |
BG |
WG |
BG |
|
|
yellow |
BY |
WY |
BY |
|
edu.uptymez.com
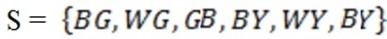
n(S) = 6
E= 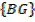
n(E)= 1
P(E)= 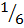
INTERSECTION
The intersection of two events A and B denoted by A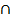 B is the event that occurs if A and B are on a single performance of the experiment.
B is the event that occurs if A and B are on a single performance of the experiment.
UNION
The union of two events A and B , denoted by A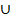 B is the event that occurs if either A or B or both occur on using performance of the experiments.
B is the event that occurs if either A or B or both occur on using performance of the experiments.
Example.
1. Consider a die toss experiment , events are defines as;
E(A)= 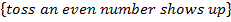
E(B)= 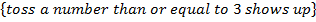
Find
(a). P(A B)
B)
(b). P(A B)
B)
Solution:
S= 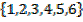
E(A) = 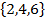
E(B)= 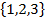
a. A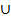 B=
B= 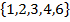
P(A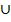 B) =
B) = 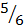
b. A B =
B = 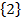
P(A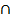 B) =
B) = 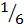
1. The probability that a man watches TV in any evening is 0.6, the probability that he listens the radio is 0.3 and the probability the does both is 0.15. what is the probability that he does neither?
Solution:
P(T) = 0.6
P(R)= 0.3
P(T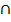 R) = 0.15
R) = 0.15
P(A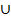 B) = P(A) + P(B) – P(AnB)
B) = P(A) + P(B) – P(AnB)
P(T R) = 0.6 + 0.3 – 0.15
R) = 0.6 + 0.3 – 0.15
= 0.75
P(TUR)1= 1- P(TUR)
= 1 – 0.75
= 0.25
2. At a second hand show room, 20% of the cars have no engine, 40% of the cars have bad tyres, and 15% have no engine and have tyres. what is the probability that a car chosen at random has good tyres and an engine?
Solution:
P(A) = 20%
P(B) = 40%
P(A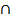 B) = 15%
B) = 15%
P(A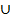 B) =
B) = 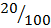 +
+ 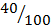 –
– 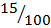
=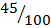
P(AΔ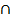 BΔ) = 100 – P(A
BΔ) = 100 – P(A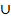 B)
B)
= (100% – 45%)
P(AΔ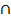 BΔ) = 55%
BΔ) = 55%
MUTUALLY EXCLUSIVE EVENTS
If one and only one event among two or more events can take place at a time, then the events are called mutually exclusive.
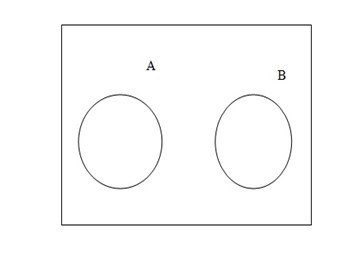
Event A and B are mutually exclusive if A B = 0 and therefore
B = 0 and therefore
P(A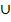 B) = P(A) + P(B)
B) = P(A) + P(B)
Example
1. Find the probability that an even number or an odd number greater than one occurs when a die is tossed once.
Solution
S = 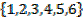
E(A) = 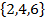
E(D) = 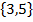
P(A D) = P(A) + P(B)
D) = P(A) + P(B)
= 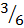 +
+ 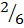
= 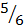
2.
In a family of four children, what is the probability that ;
a) Two are boys and two are girls.
b) All are boys
c) Exactly 4 are girls
d) At least 4 are boys
Solution
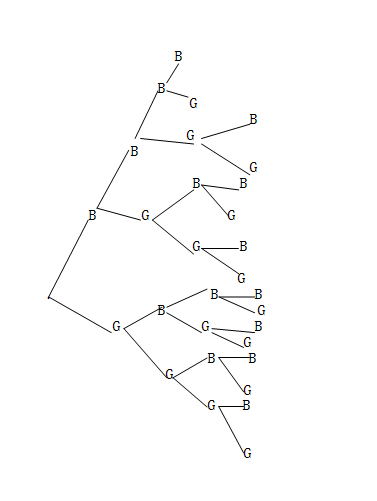
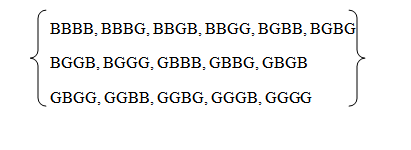
(a) All are boys and two are girls
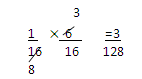
(b) All are boys
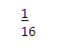
(c) Exactly four are girls
(d) At least four are boys 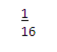
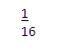
INDEPENDENT EVENTS
Two events are independent if the occurrence of one event or non occurrence of the event does not affect the probability of the other event.
P(E1 and E2 ) = P(E1) – P (E2)
Or P(E1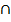 E2)
E2)
Exercise
1. If the probability that A will be alive in 20 years is 0.7 and the probability that B will be alive in 20 years is 0.5, then the probability that they will both be alive in 20 years is ?
Solution
P (A B) = P(A) x P(B)
B) = P(A) x P(B)
= 0.7 x 0.5
= 0.35
2. The probabilities that Halima and perpetuate will be selected for further studies are respectively 0.4 and 0.7. Calculate the probability that both of them will be selected for further studies.
Solution
P (A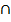 B) = P (A) x P(B)
B) = P (A) x P(B)
=0.4×0.7
=0.28
3. One bag contains 4 white balls and 2 black balls , another contains 3 white balls ad 5 black balls. If a ball is drawn from each bag , find the probability that
a. Both are white
b. Both are black
c. One is white and one is black.
Solution:
a. P(w1w2) = P(w1) x P(w2)
=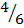 x
x 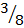
=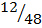
= 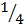
b. P(B1+B2)= P(B1) P(B2)
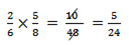
c. (w1 B2 or B1w2)= P (w1) x P( B2) + P(B1) x P(w2)
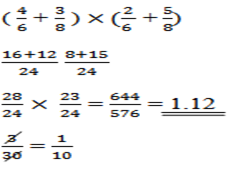
DEPENDENT EVENTS
Events are dependent when one event affects the probability of the occurrence of the other.
P (E1/E2) = P(E1) x P(E1/E2)
Not replaced P(RWB) = P(R) x P(W) x P (B)
= 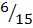 x
x 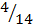 x
x 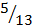
Exercise
1. The probability that a man and his wife will be alive for fifty years are 3/10 and 1/3 respectively. Find the probability that
a. both will be alive,
b. At least one will be alive.
Solution:
(a) P(A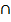 B) = P(A)x(PB)
B) = P(A)x(PB)

(b)
2. A fair die is tossed once and the number showing up is recorded. find the probability of an even number greater than two showing up.
Solution:
S = 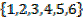
E = 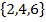
P(E) = 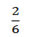
=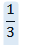
3. A box contain 4 white balls and 5 black balls. two balls are drawn at random from the box. Find the probability that both the balls are
a. white
b. black
solution:
a. P(A1/A2) = P(A)
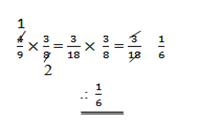
b. 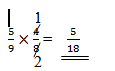
THE MULTIPLICATIVE RULE
Permutations;
A permutation of ‘n’ different objects taken ‘r’ at time is an arrangement of ‘r’ out of ‘n’ objects with attention given to the order of arrangement. the number of permutations of ‘n’ objects taken ‘r’ at a time is denoted by;
nPr or nPr = 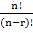
Example
1. The number of permutations of the letters a, b, c taken two at a time is;
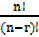 = 3P2 =
= 3P2 = 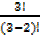 =
= 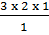
These are ab, ba, ac, ca bc, cb.
2. In how many ways can 10 people be seated on a bench if only 4 seats are available?
Solution
10P4 = 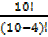 =
= 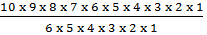
= 5040way
3. Evaluate
8P3 = 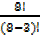
=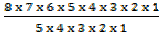
= 336ways
4. How many four digits numbers can be formed with 10 digits 0,1,2,3,4,5,6,7,8,9
a. Repetition is allowed.
b. Repetitions are not allowed.
Solution
a. P1 P2 P3 P4
10 10 10 10
= 10 x10x10x10
= 10000 ways
b. P1 P2 P3 P4
10 9 8 7
= 10x9x8x7 = 5040ways
NOTE : the number of permutations of ‘r’ objects consisting of groups of which n1 are alike and n2 are alike is
 where n = n1 + n2
where n = n1 + n2
COMBINATIONS
Combinations of n different objects taken ‘r’ at a time is a selection of ‘r’ out of the ‘n’ objects . take ‘r’ at a time denoted by;
nCr = 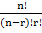
Example
1. The number of combination of letters a,b,c taken two at a time.
Solution
3C2 = 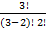
= 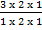
=3
These are ab, bc and ac
NOTE ab, ba are the same.
2. How many arrangements are there of the letters of the word “solopaga”?
Solution
n =8
n1 (0) = 2
N2 (A)= 2
No arrangement = 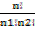
= 
= 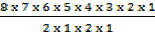
= 10080
3. It is known that nCr = nCn-r
Find x given that 20C18 = 20Cx
Solution
20Cx= 20C20-18
= 20C2
x = 2
4. A box contains 8 red,3 white and 9 blue balls. If 3 balls are drawn at random , determine the probability that;
a. All 3 are red
b. All 3 are white
c. 2 red and one white
d. 1 of each color is drawn
e. At least one is white.
Solution
a. P(R1R2R3) = 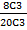
8C3 = 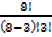 =
= 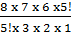 = 56
= 56
20C3= =
=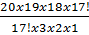 =1140
=1140
P(R1R2R3) = 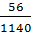
b. P(W1W2W3) = 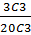
3C3 = 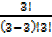 =
= 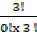 = 1
= 1
Note: 20C3=1140
P(W1W2W3) = 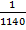
c. P(R1R2) = 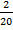 x
x 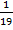 =
= 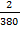 =
= 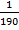
P(1W) = 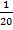
P(R1R2) and P(1W) = P(R1R2) x P(1W) = 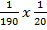 =
= 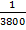
d. P(RWB) = 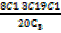
= 
= 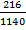
e. P( W1 W2 W 3)+ P(W1 W2W3)+ P(W1 W2W3)
= 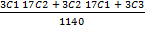 =
= 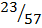
= 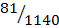
5. A jar contains 3 white peas, 2 red peas and 2 yellow peas. Three peas are drawn at random ,find the probability that;
a. At least 2 peas are white
b. Exactly 2 peas are white.
Solution
a. P(W1W2W3) + P (W1W2W3)
= 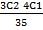 +
+  =
= 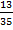
b. P(W1 W2W3)
= 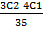 =
=