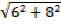Displacement and Position Vectors.
Displacement
Examples of vector quantities are displacement, Velocity, acceleration, force, momentum, electric field and magnetic field.
Quantities which have magnitude only scalars, for example distance, speed, Pleasure, time and temperature.

Sometimes a single. Small letter with a bar below like a or a like a
These are physical quantities which have magnitude and direction
vector quantities – have both magnitude and direction ie velocity , acceleration etc.
Scalar quantities – are quantities which only have magnitude but nit direction. ie size, mass , time….etc
Naming vectors
(i). capital letters OA

(ii). small letter a
(iii). small letter with bar
a , b
1. Equivalent vectors
Two vectors are equivalent if they have the same magnitude and direction.
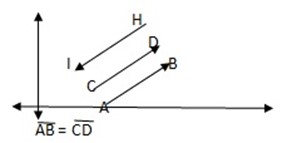

 HI is not equivalent to AB and CD
HI is not equivalent to AB and CD
2. displacement vector
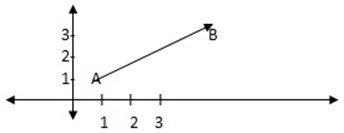
1. position vector
In the xy plane all vectors having their initial Points at the origin and their end Points elsewhere are defined as position vectors. Position vectors are named by the coordinates of their end points
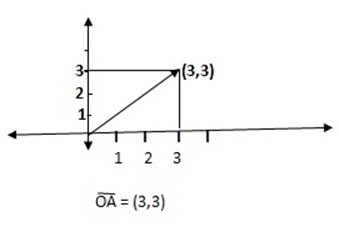
OA = (3,3)
4. unit vector.
In the xy plane the position vector of unit length in the positive x-axis direction is named i and the position vector of unit length in the positive y-axis direction is named j.
Both i and j are Unit Vectors.
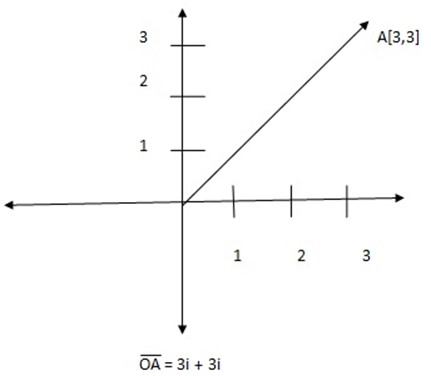
Questions
1. write the following vectors as position vectors.
a. a ( -3,-4) = ( -3, 0) + ( 0,-4)
= -3(1,0) + -4 (0,1)
= -3i -4j
b. b ( -5, 5) = ( -5, 0) + ( 0,5)
= -5 ( 1,0) + 5(0,1)
= -5i + 5j
c. c = ( -1, 6)
= (-1,0) + ( 0,6)
= -1 ( 1,0) + 6( 0,1)
= -1i + 6j
Alternative = -i + 6j
2. write the following vectors as position vectors
a. S = – 8 i
= -8i + 0j
= -8 ( 1,0) + 0( 0,1)
= ( -8,0)
b. u = 7j
u = 0i +7 j
= 0( 1,0) + 7 ( 0,1)
u = (0,7)
Exercise
1. express the following vectors in form of I and j vectors
(a)
P ( -3,6)
= ( -3, 0) + ( 0,-6)
= -3 ( 1,0) + 6 ( 0,1)
= -3i + 6j
(b)
q = ( 5 , -2)
= ( 5,0) + ( 0,-2)
= 5( 1,0) + – 2( 0,1)
= 5i – 2j
(c)
r = (-4 , 2)
r = (4,0) + (0,2)
= -4(1,0) + 2 ( 0,1)
= -4i + 2j
3. express each of the following in a position vector
(a). a = 3i + 2j
= 3( 1,0) + 2( 0,1)
= (3,0) + ( 0,2)
= ( 3,2)
(b). b = 6i – 7j
= 6( 1,0) – 7 ( 0,1)
= ( 6,0) + ( 0,-7)
= ( 6,-7)
(c). e = -3i
= 0 (1,0) + ( 0,-3)
= (0,-3)
MAGNITUDE (MODULUS) OF A VECTOR
The magnitude of vectors is used to define the size of a vector. The other name for magnitude is modulus.The magnitude or modulus of a vector is a scalar quantity.
Consider the position vector r = (x, y)
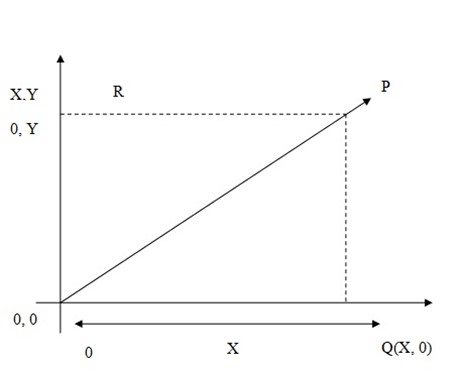
Vector OP = r = (x,y)
OP is perpendicular to the x-axis
PR is perpendicular to the y-axis
Triangle OPQ is right angled at Q
By Pythagoras theorem
PQ2= OQ2 + QP2
OP2= x2 + y2
OP = 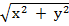
If r = ( x,y) then
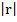 =
= 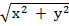
this is the formula for finding the magnitude
Example;
Calculate the magnitude of the position vector
v = (-3, 4)
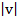 =
= 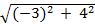
= 5
Unit vector
If U is any vector, the unit vector in the direction of u is given by
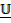 and is denoted as
and is denoted as 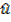
Example
Find the unit vector in the direction of the vector u= (12,5)
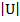 =
= 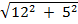 = 13
= 13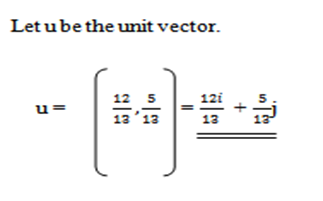
Exercise
1. define the magnitude of a vector hence calculate the magnitude of
a= -12i – 5j
solution
a= -12i 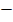 5j
5j
= -12( 1,0) -5( 0,1)
= (-12,0) + (0,-5)
= ( -12,-5)
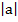 =
= 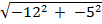
= 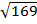
= 13
2. a. find i + j
= 1,1
= 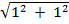
= 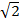
SCALAR MULTIPLICATION
Example;
1. if a = 3i + 3j and 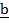 = 5i + 4J find, -5a + 3b
= 5i + 4J find, -5a + 3b
= -5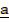 + 3
+ 3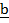
= -5 (3i + 3j) + 3( 5i +4J)
= -15i -15j + 15i + 12j
= -3j
2. given 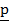 = ( 8,6) and
= ( 8,6) and 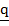 = ( 7,9)
= ( 7,9)
Find 9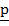 – 8
– 8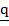
= 9 ( 8,6) – 8( 7,9)
= (72,54) – (56 , 72)
= (16,-18)
3. given vector a = –i + 3j , b = 5i -3j and c = 4a + 3b
(a) find the magnitude of vector c
(b) find the unit vector in the direction of vector d where d =2a + -3b + c
solution;
(a) c = 4a + 3b
= ( –i + 3j ) + 3 ( 5i – 3j)
= -4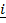 + 12
+ 12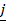 + 15
+ 15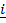 – 9
– 9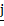
= 11i + 3j ( 11,3)
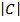 =
= 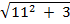
= 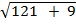
= 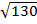
b.d = 2a – 3b
+ c
= 2( -i + 3j ) -3 (5i +- 3i ) + 11i + 3j
= -2i + 6j -15i + 9j + 11 i + 3j
= -2i -15i + 11i + 6j + 3j + 9j
= -6i + 18j
( -6 , 18)
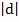 =
= 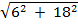
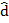 =
= 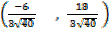
ADDITION OF VECTORS
The sum of any two or more vectors is called the resultant of the given vectors.
here we have 3 laws which govern us.
Resultant is the one which represents the sum of vectors.
1. THE TRIANGLE LAW
The initial point of the second vector is joined to the end points. The first vector, resultant is joined by completing the triangle whose initial point is the initial point of the first vector and its end point concedes with that of the second vector.
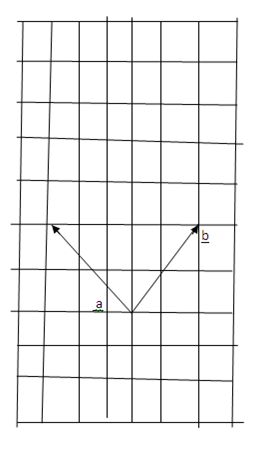
82
= 10
Cos α = 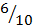
Cos B = 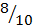
Hence 0.6 and 0.8 are direction cosine of a
Cos α = 0.6
α= 53016′
Exercise:
(1) Evaluate the magnitude and direction of b= -8i + 6j
Solution
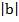 =
= 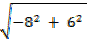
= 10
Cos α= 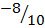 = 0.8
= 0.8
Cos B = 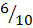
Cos B = 0.6
B = 5303′
2. Calculate the direction cosines of c = 3i + 4j , hence show that the sum of the squares of these direction cosines is one.
Solution
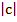 =
= 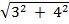
= 5
Cos α = 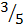 = 0.6
= 0.6
Cos B = 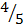 = 0.8
= 0.8
0.62+ 0.82 = 1
1.00 = 1
1 = 1
3. Find the direction cosine of
(a) a = i+ j
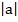 =
= 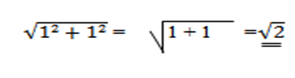
Cos α = 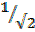 x
x 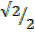 =
= 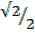
Cos B = 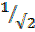 x
x 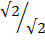 =
= 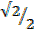
The direction of cosine a is 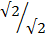
4. given a = ( 1,2 ) b = ( -2,-1) and c = ( 3,7)
Calculate 2a + 3b + 4c
Solution
= 2(1,2) + 3( -2,-1) + 4( 3,7)
= (2,4) + (-6,-3) + (12,28)
= (8,29)
BEARING
1. Two methods used in reading bearing of all angles are measured with reference from the north direction only.
North is taken as 0000 , east as 0900, south as 1800, and west as 2700.
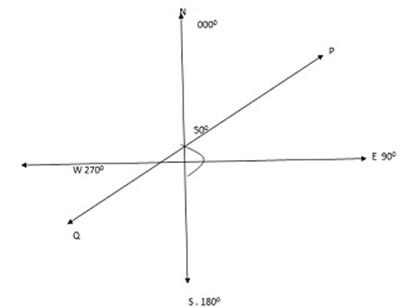
Point p located at a bearing of 0500. Point Q is located at a bearing of 2000.
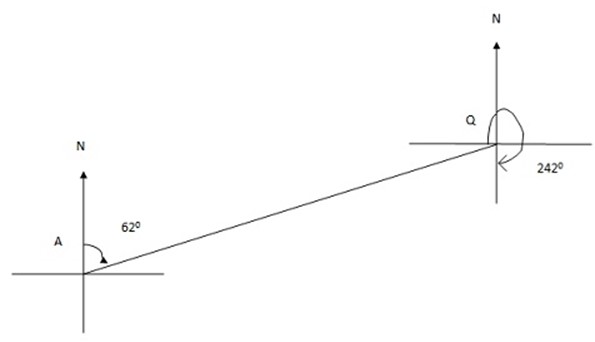
Bearing of point B from point A is measured from north direction at point A to the line joining AB ( bearing of point B from A is 0620)
Bearing of A from B is measured from the north direction at B to the line joining BA.
(Bearing of A from B is 2420)
Application of vectors
Questions:
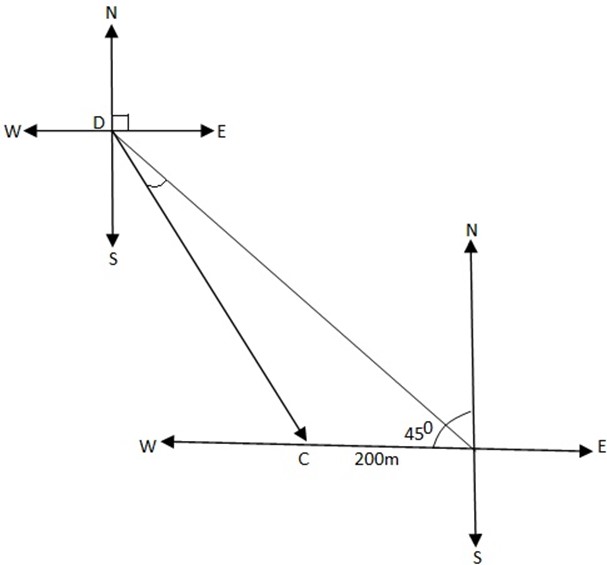
1. a student walks 400m in the direction of S450E from the dormitory to the parade ground and then he walks 100m due west to his classroom. Find his displacement from the dormitory to the classroom.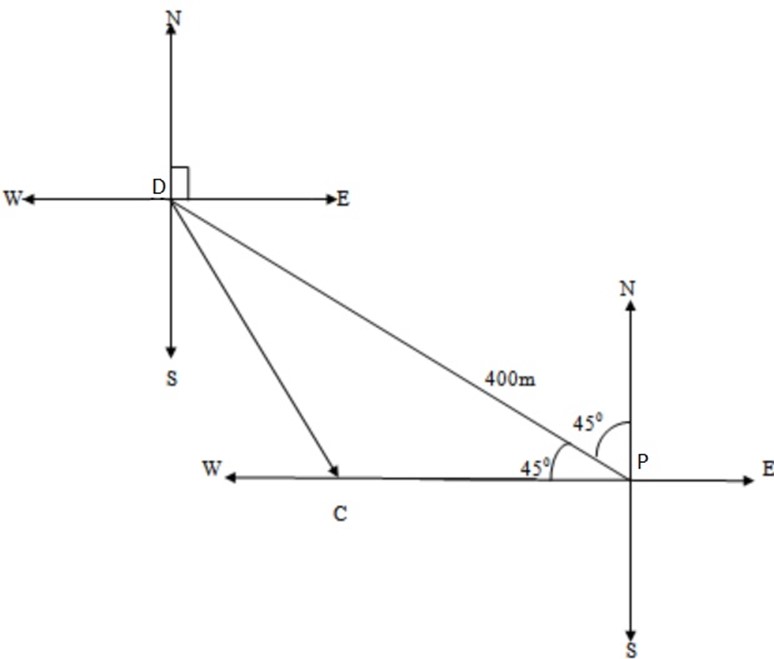
From figure above the resultant is 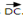 . By the cosine rule.
. By the cosine rule.
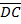 2 = 4002 + 1002 – 2 x 400x 100cos 450
2 = 4002 + 1002 – 2 x 400x 100cos 450
= 160000 + 10000- 80000 x 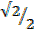
= 170000 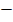 56568.5
56568.5
=113440
From figure above the resultant is 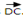 By the cosine rule.
By the cosine rule.

Bearing = S(450 – 120 )E = S330E.
The boy displacement from the dormitory to the classroom is 336.8metres at a bearing of S330E
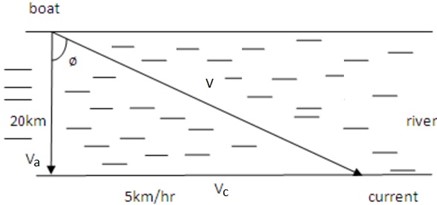
2. A boat crosses a river at velocity of 20km/ hr southwards. The river has a current of 5km/hr due east. Calculate the resultant velocity of the boat.
Solution
Solution
Let the velocity of the boat be v that of the current y and the resultant velocity v
Let ø be the angles between v and vb
Rr = 5i – 20j
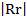 =
= 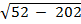
= 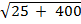
= 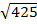
Let θ be the angle between v and vb.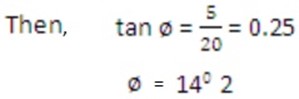
|
No. |
logarithm |
|
(4.25 x 102 )1/2 2.002 x 101 |
2.6284 2 1.3142 |
edu.uptymez.com

3. A student walks 500m in the direction S 450E from the classroom to the basketball ground and then she walks 200m due west to the dormitory. What Is her displacement from the classroom.
Solution
= 650000 – 200,000x 1.414
= 290,000- 282800
=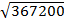
|
No. |
Logarithm |
|
(3.672x 105)1/2 63639 |
5.5649 2 2.782445 |
edu.uptymez.com
= 636
4. An aeroplane flies with the speed of 100km/ hr and the wind is blowing from south with speed 40km/hr.
(a). find the time used by an aeroplane to fly due north the distance 70km.
(b). in what bearing must the pilot set his plane in order to fly due east.
(c). find the resultant speed of an aeroplane to fly east in the nearest km/hr and time taken to fly t he distance 296 km due east.
Solution
(a)
v = 100km/hr + 40km/hr = 140km/hr
Time = d/v
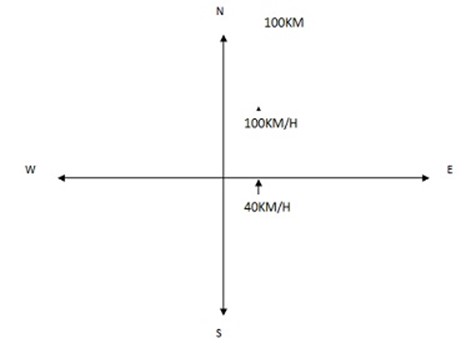
= 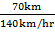
= 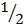 hr
hr
100KM
(b). cos θ= 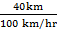
1002 = 402 + X2
10000- 16000= X2
X = 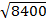
|
No. |
Logarithm |
|
( 8.4 x 103) ½ 9.164x 101 |
3.9243 2 1.9621 |
edu.uptymez.com
Resultant (s) = 91.64 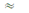 92
92
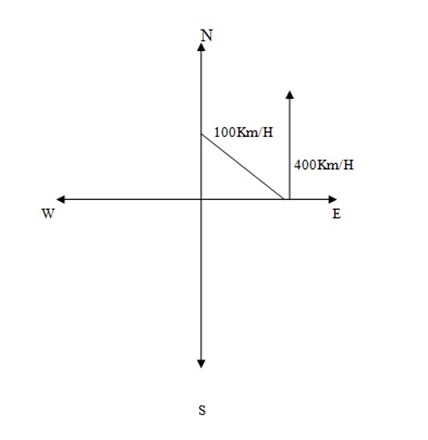
T = D / V
= 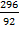
= 3.217
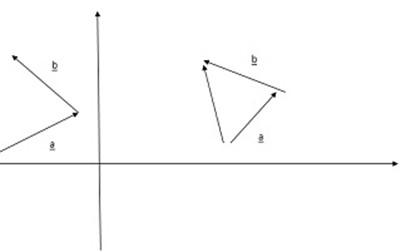
2. THE PARALLELOGRAM LAW
 Two vectors sharing a common initial point P to get the resultant we should complete a parallelogram.
Two vectors sharing a common initial point P to get the resultant we should complete a parallelogram.
Example;
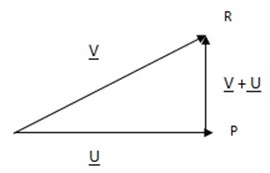
PR = U + V = V + U
3. THE POLYGON LAW OF VECTOR ADDITION.
Here the resultant is obtained by joining endpoint to initial point of the vector one after another.
The resultant is the vector joining the initial point of the first vector to the end point of the second vector.
Exercise 5.3
1. given the vectors p, q, r, s and t in the figure.
Find (a). P+Q
(b). P+Q+R
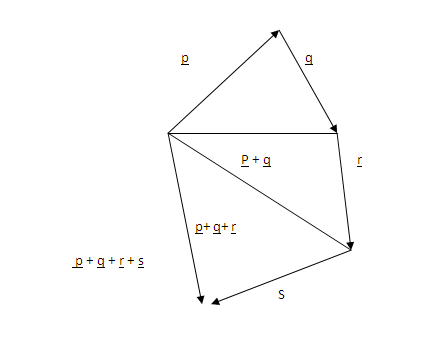
(c). P+Q+R+S
Solution
a.
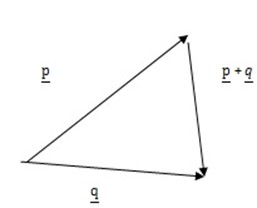
b.
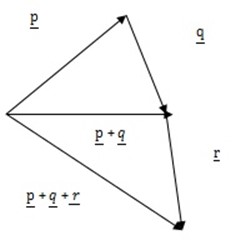
c.
DIRECTION OF A VECTOR
1. DIRECTION COSINE
Consider a vector 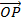 = ( X, Y)
= ( X, Y)
OP makes angle α with the positive direction along the direction of the y-axis
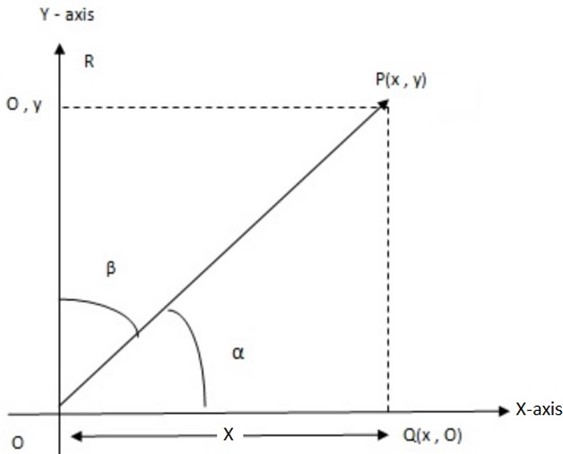
Triangle OQP is right angled at Q
P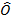 R = O
R = O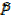 Q (alternate interior angle)
Q (alternate interior angle)
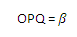
Cos α = 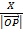
Cos B = 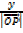
The values of cos α and cos B are the direction cosines of vector 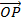
Example
1. If a = 6i + 8j
Find the direction cosines of a , hence
Find the angle that a makes with the positive axis.
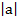 =
=