INDUCTIVE REACTANCE
Inductive reactance is the opposition in which an inductor offers to current flow. It is denoted by XL
Inductance not only causes the current to lag behind the voltage but it also limits the magnitude of current in the circuit.
We have seen above that,
Io = 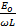
ωL = 
Clearly the opposition of inductance to current flow is ωL. This quantity ωL is called inductive reactance XL of the inductor.
Inductive reactance XL
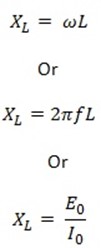
a) From
XL = 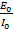
But 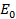 =
= 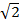
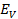 and Io =
and Io = 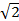
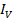
Then,
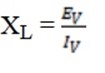
XL = 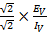
b) For d.c
f = 0
so that,
XL = 2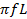
XL = 2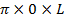
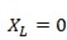
Therefore a pure inductance offers zero opposition to d.c
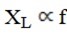
c) XL = 2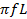
Therefore,the greater f,the greater is XL and vice versa.
d) We can show that the units of XL are that of ohm
XL = ωL = 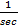 x Henry =
x Henry = 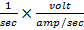 and
and
XL = 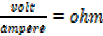
III) Average Power consumed
E =  sin ωt
sin ωt
I = 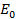 sin (ωt-
sin (ωt- I = –
I = –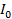 cos ωt
cos ωt
Instantaneous power P
P = EI
P = (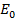 sin ωt) (-
sin ωt) (-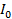 cos ωt)
cos ωt)
P = –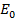
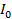 sin ωt cos ωt
sin ωt cos ωt
P = 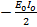 Sin 2ωt
Sin 2ωt
Average power P is equal to average of power over one cycle.
P =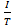
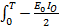 Sin 2ωtdt
Sin 2ωtdt
P = 0
Hence average power absorbed by pure inductor is zero
During one quarter cycle of alternating source of e .m .f. energy is stored in the magnetic field of the inductor this energy is supplied by the source.
During the next quarter cycle the stored energy is returned to the source. For this reason average power absorbed by a pure inductor over a complete cycle is zero.
NUMERICAL EXAMPLES
1. A pure inductive coil allows a current of 10A to flow from a voltage of 230V and frequency 60Hz supply.
Find
i) Inductive reactance
ii) Inductance of the coil
iii) Power consumed
Write down equations for voltage and current:
Solution
EV = 230V
IV = 10A
f =50Hz
i) Inductive reactance XL
XL = 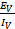 =
= 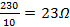
ii) Inductance of the coil L
From
XL =2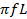

L = 0.073 H
iii) Power absorbed = 0
Also
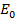 = 230 x
= 230 x 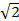
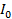 = 10 x
= 10 x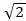
 = 325.27V
= 325.27V 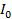 = 14.14A
= 14.14A
ω = 2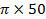
ω = 314
Since in pure Inductive circuit current lags behind the applied voltage by  radians. The equation for voltage and current are,
radians. The equation for voltage and current are,
E = 325 .27 sin 314t, I = 14.14 sin (314t)
2. Calculate the frequency at which the inductive reactance of 0.7H inductor is 220Ω
Solution
XL = 220 Ω
L = 0.7H
f =?
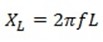
f =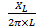
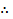 f = 50 Hz
f = 50 Hz
3. A coil has self inductance of 1.4H. The current through the coil varies sinusoidally with amplitude of 2A and frequency 50 Hz
Calculate
i) Potential difference across the coil
ii) r .m .s value of P.d across the coil.
Solution

(i) P.d across the coil
E = L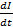
E = L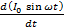
E = L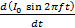
E = L  cos
cos  t,
t,
E = L 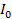 2
2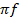 cos2
cos2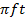
E = 2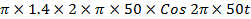
E = 880 cos 100 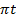
ii) r.m.s value of potential different across the coil
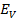 =
= 
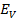 =
= 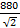
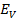 = 622.2V
= 622.2V
4. How much inductance should be connected to 200V, 50 Hz a.c supply so that a maximum current of 0.9A flows through it?
Solution
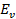 = 200V
= 200V
Io = 0.9A
f = 50 Hz
Peak value of voltage 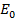
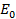 =
=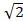
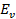
 =
= 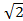
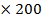
Inductive reactance L
XL = 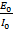
XL = 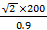
XL = 314.27 Ω
Inductance L,
L = 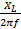
L= 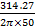
L = 1 H
5. An Inductor of 2H and negligible resistance is connected to 12V, 50Hz supply. Find the circuit current, what current flows when the inductance is changed to 6H?
Solution
* For the First case XL
XL = 2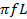
XL = 2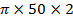
XL = 628 Ω
Circuit current
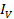 =
= 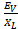
= 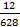
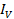 = 0.019A
= 0.019A
* For the second case XL‘
XL‘ = 2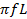
XL‘ = 2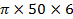
XL‘ = 1884 Ω
Circuit current
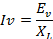
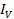 =
= 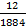
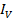 = 0.0063A
= 0.0063A