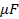FORM 6 PHYSICS: AC THEORY PART 3

A.C CIRCUIT CONTAINING CAPACITANCE ONLY

When an alternating voltage is applied to a capacitor, the capacitor is charged first in one direction and then in the opposite direction.

The result is that electrons move to and fro round the circuit connecting the plates, thus constituting alternating current.

Consider a capacitor of capacitance C connected across an alternating source of e .m. f .

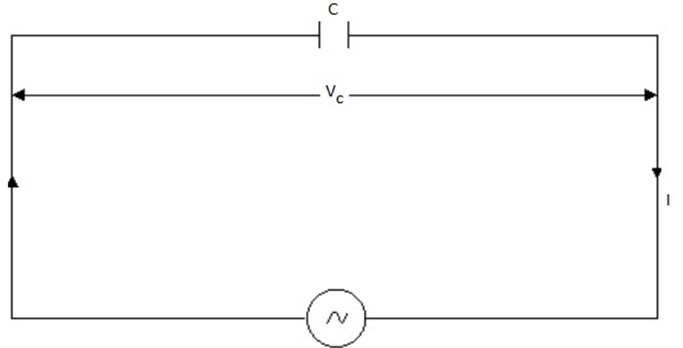
Suppose the instantaneous value of the alternating e.m.f   E is given by

E = 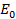sin ωt …….. (i)

If I is the current in the circuit and Q is the charge on the capacitor at this instant, then the Potential difference across the capacitor V_C

          

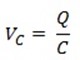
 At every instant the applied e.m.f E must be equal to the potential difference across the capacitor.

    E =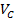                              

                                          

    Q = C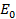 sin ωt

From,
I =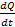

I =

I = Cωcos ωt

I = Cω 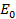sin (ωt + 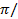2

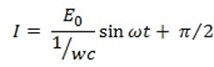
The value of I₀ will be maximum Io when sin (wt+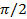) = 1
           

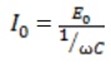
Substituting the value of I_o in equation (ii)

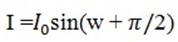
1) Phase Angle

It is clear from equation (I) and (ii) that circuit current leads the applied voltage by π/2 radians or 90Ëš.

This fact is also indicated in the wave diagram.

 

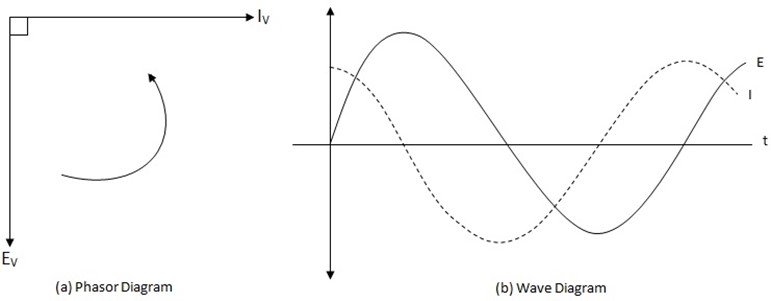
It also reveals that I_v leads E_v by 90°, hence in a.c circuit current in capacity leads the voltage.
This means that when voltage across capacitor is zero, current in capacitor is maximum and vice versa.
When P.d across capacitor is maximum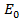, the capacitor is fully charged, i.e circuit current is zero.
Since the rate at which a sinusoidally varying p.d falls is greater as it reaches zero, the current has its maximum value when P.d across capacitor is zero.  Hence, current and voltage are out of phase by 90°.

                      CAPACITIVE RESISTANCE

Capacitive resistance is the opposition which a capacitor offers to current flow.  It is denoted by X_C.

 Capacitance not only causes the voltage to lag behind the current but it also limits the magnitude of current in the circuit.

We have seen above that

=  

 =

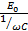
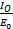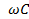
Then

Clearly, the opposition offered by capacitance to current flow is 1/ωC

The quantity 1/ωC is called capacity reactance X_C of the capacitor

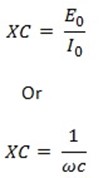
X_C will be in Ω if f is in Hz and C in Farad

a) From

  =

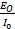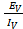
Then

 =

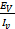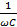
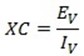
b) For d.c

f = 0
X_C =  =

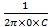
X_C =  

X_C = ∞

Therefore a pure capacitance offers infinite opposition to d.c.  In other words, a capacitor blocks d.c.

c. From
X_C =

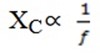
Therefore the greater the f the  smaller is X_C and vice versa

d)  From

Therefore the units X_C are Ohm

(iii) AVERAGE POWER ABSORBED

From

E = 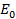sin ωt

I = 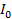sin (ωt+2)

I = 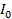cos ωt

Instantaneous power P

P = EI

P = 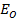Sin ωt. 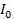Cos ωt

P = 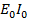(sinωtcosωt)

P = 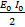Sin 2ωt

∴  Average power P = Average of  P Over one cycle

P =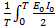Sin 2ωtdt

P = 0

Hence average power absorbed by pure capacitance is zero.
During one quarter cycle of the alternating source of 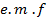 energy is stored in the electric field of the capacitor.

This energy is supplied by the source during the next quarter cycle, the stored energy is returned to the source

                        WORKED EXAMPLES

1. A 318μF capacitor is connected 230V, 50Hz supply.  Determine

i) The capacitive reactance

ii) r.m.s value of circuit current

iii) Equations for voltage and current

Solution

C = 318μF = 318 x 10^-6 F

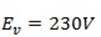
f = 50 Hz

i) Capacitive reactance X_C

X_C =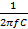

X_C =  

X_C = 10 Ω
ii) r.m.s value of current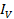

 = =

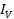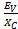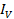= 23A

iii )
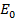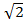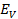
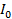= .         = √2 x 23

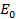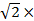= 230 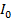      = 32.53A

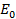= 325.27 V

ω= 2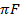

ω = 2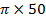

ω= 314

E₀ = 325.27sin 314t and I = 32.53 sin314t

2. A coil has an inductance of 1H

a) At what frequency will it have a reactance of 3142Ω?

b) What should be the capacitance of a condenser which has the same reactance at that frequency?

Solution

a) L = 1H

X_L = 3142Ω

f   = ?

X_L = 2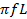

f =    = :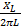

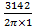f= 500Hz

b) X_C = 3142 ,      f=500 Hz

C =?
X_C =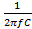

C =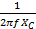  

C =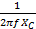

C = 0.11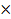 

C = 0.11

3.  A 50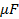  capacitor is connected to a 230V, 50Hz supply.  Determine

i)  The maximum charge on the capacitor

ii)  The maximum energy stored in the capacitor

Solution
The charge and energy in capacitor will be maximum when p.d across the capacitor is maximum.

i)  Maximum charge on the capacitor

Q = C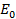

Q = C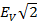

Q = (50x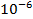) x (230 x)

Q = 16.26 x 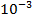C

ii) Maximum energy stored in the capacitor U

U =  C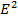

U = 1/2 x (50x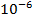) x (230 x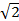 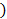     ²

U = 2.65J

4. The Instantaneous current in a pure inductance of 5H is given be

I = 10sin (314t- 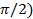amperes

A capacitor is connected in parallel with the inductor.  What should be the capacitance of the capacitor to receive the same amount of energy as inductance at the same terminal voltage?

Solution
The current flowing through pure inductor is

I = 10 Sin (314t)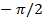

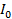= 10A

ω = 314s^-1

Maximum energy stored in the inductor

U_L = 250J ………. (i)

Now

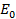= ωL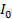

= 314 x 5 x 10

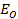= 15700v

Max energy stored in the capacitor of capacitance C

=  

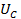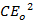
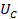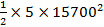= ……….(ii)

Equate the equation (I and (ii)

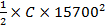=  = 250

C =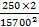

C = 2.03 x F

C = 2.03