FORM 6 PHYSICS: AC THEORY PART 4

A.C CIRCUIT CONTAINING R AND L IN SERIES

Consider a resistor of resistance R ohms connected in series with pure inductor of L Henry.

Let

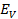= r.m.s value of applied alternating e.m.f

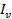=r.m.s value of the circuit current

V_R = 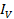R when V_R is in phase with

V_L = 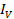 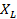 where 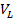leads  by 90º

Taking current as the reference phasor, the phasor diagram of the circuit can be drawn as shown in figure.

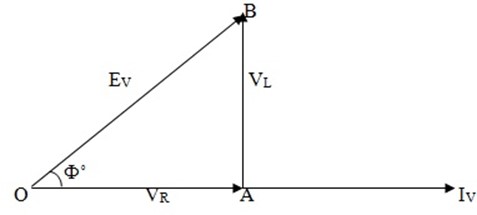
The voltage drop V_R is in phases with current and is represented in magnitude and direction by the phase OA.

The voltage drop V_L leads the current by 90º and is represented in magnitude and direction by the phase AB.

The applied voltage 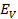 is the phasor sums of these two voltage drops

=  +

=

=

=

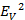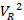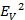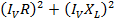
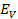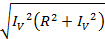
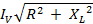
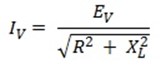
1) Phase Angle

It is clear from the phasor diagram that circuit current 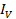lags behind the applied voltage  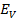by Φº.

Therefore we arrive at a very important conclusion that in an inductive circuit current lags behind the voltage.

NUMERICAL EXAMPLE

      1. Three impedance are connected in series across a 200V, 50Hz  supply. The first impedance is a 10┦ resistor and the second is a coil or 15 ┦ inductive reactance and 5 ┦ resistance while the  third  consists of a 15 ┦ resistor  in series with a 25┦ capacitor

Calculate

i)  Circuit  current

ii)  Circuit phase angle

iii)  Circuit  power factor

iv)  Power consumed

Solution

i)  Total circuit Resistance

R = 10 +5 + 15

R = 30 ┦

Total Circuit reactance

X = X_L – X_C

X = 15 – 25

X = -10 ┦ (capacitive)

Circuit impedance Z

            

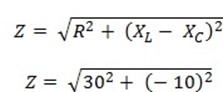
              Z = 31. 6 ┦

Circuit current I_V

        I_V = E v
                 Z

      I _V = 200
               31.6

        I_V = 6. 33 A

ii)  Circuit phase Angle

iii)   Circuit power factor

Power factor = COS θ

          = COS 18 .26º

 Power factor = 0. 949

iv)  Power consumed   P

       P = E_V I_V Cos ∅

       P = (200 x 6.33) x 0. 949

      P = 1201. 4 W

Alt

    P = I_v² R

2.   A 230V, 50Hz supply is applied to a coil of 0.06 H inductance and 2.5 Ω resistance connected in series with 6.8 μF capacitor

Calculate

i.    Circuit  impedance

ii.   Circuit current

iii.  Phase  angle  between  E_V and  Iv

iv.   Power factor

v.    Power  consumed

Solution

i) Inductive reactance X_L

X_L = 2ΠfL

X_L = 2Πx 50 x 0.60

X_L = 18 .85 Ω

Capacitive reactance X_C

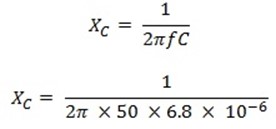
X_C = 468 Ω

Circuit Impedance

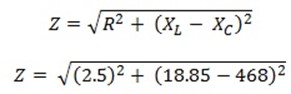
      Z = 449. 2 Ω

ii) Circuit current I_V

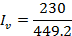
I_V = 0.152 A

iii) Phase angle between E_V and I_V

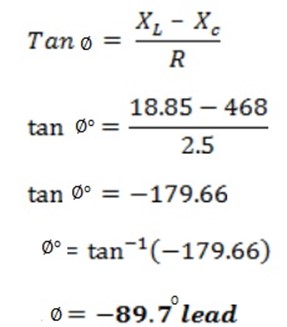
iv)  Power factor

 Cos Φ = 0.0056

v)   Power consumed  P

P = E_VI_S Cos Φ

P = 230.x 0.512 x 0.0056

P = 0.66 W

3.   A resistance R, and inductance L = 0.01H and a capacitance C are connected in series. When an alternating voltage E = 400Sin (3000t- 20⁰) is applied to the series combination, the current flowing is 10√2 Sin (3000t – 650). Find the value of R and C

Solution

The circuit current lags behind the applied voltage by θ

θ = 65⁰ – 20

θ = 45⁰

This implies that the circuit is inductive i.e. 

       X_L > X_C

The net circuit reactance X

         X = X_L –X_C

Now

X_L = ωL

X_L = 3000 x 0.01

X_L = 30 Ω

Also

From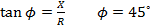

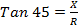
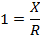
Circuit Impedance Z

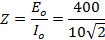
Z = 28.3 Ω

Now

Z² = R² + X²

Z = R² + R²

Z² = 2R²

Z = R √2

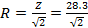
R = 20Ω

Now

X = X_L – X_C

20 = 30 – X_C

X_C= 10Ω

From

C = 33.3 x 10 ^-6 F

4.  A series RLC circuit is connected to an a.c (220V, 50 H) as shown in the figure below

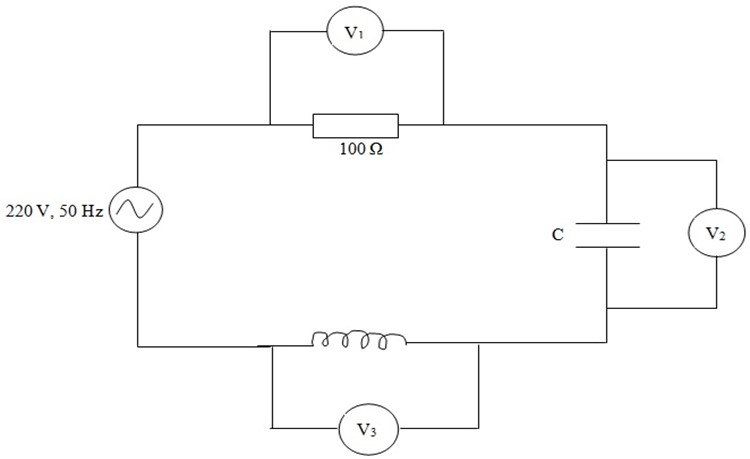
If the reading of the three volt meter V₁  V ₂ and V₃ are 65V, 415V and 204V respectively.

Calculate

i.  The  current in the  circuit

ii.   The value  of inductor L

iii.  The value of  capacitor  C

Solution

Here voltmeters are considered ideal i.e. having infinite resistance.

Therefore, it is a series RLC circuit

i) Circuit current I_V

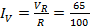
I_V = 0. 65 A

ii) Inductive reactance X_L

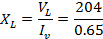
   X_L = 318. 85 Ω

      Inductance   L

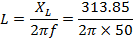
           L = 1H

iii) Capacitive reactance X_C

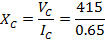
       X_C = 638. 46Ω

Capacitance   C  

  

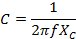
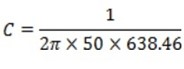
C = 5 x 10^-6 F

5.  A coil of resistance 8Ω and inductance 0.03H is connected to an a.c supply of 240V, 50 Hz.

Calculate

i)  The current the power and power factor.

ii) The value of a capacitance which when connected in series with the above coil causes no change   in the value of current and power taken from the supply

Solution
i) Reactance of the coil X_L

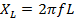
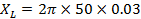
X_L=9.42 Ω

Impedance of the coil Z

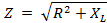
Z = 12. 46 Ω

  Circuit Current I_V

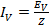
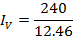
 I_V = 19.42 A

 Power consumed

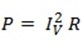
P= (19.42)² x 8

P= 3017 W

Power factor Cos Φ

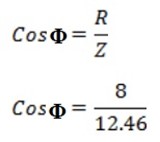
  Cos Φ =  0.65  lag

ii) To maintain the same current and power, the impedance of the circuit should remain unchanged. Thus the value of capacitance in the series circuit should be such so as to cause the current to lead by the same angles as it previously lagged.

This can be achieved if the series capacitor has  a capacitive reactance equal to twice the inductive reactance.

X_C = 2X_L

X_C = 2 x 9 .42

X_C = 18.84 Φ

Now

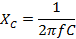
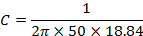
 C = 169 x 10^-9 F