FORM 6 PHYSICS: AC THEORY PART 4

RESONANCE IN R – L – C SERIES A.C CIRCUIT

The R- L – C series A.C circuit is said to be in electrical resonance when the circuit power factor is unity

X_L = X_C

 This is called series resonance.

Resonant frequency

 This is the frequency at which the reactance of the coil has the same magnitude and so giving the current in a circuit its maximum value.
X_L = X_C

where

X_C = capacitive reactance

      X_L= inductive reactance

The frequency at which resonance occurs is called the resonant frequency

The resonance in  R – L – C  series circuit can be achieved by changing  the supply frequency because  X_L and  X_C are frequency dependent

At a certain frequency, called the resonant frequency f_o, X_L becomes equal to X_C and resonance occurs.

At resonance

X_L = X_C

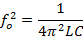
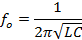
If L and C are in Henry and farad respectively, then ƒ_o will be in Hz

EFFECTS OF SERIES RESONANCE

When series resonance occurs, the effect on the circuit is the same as though neither inductance nor capacitance is present.

The current under this condition is dependent solely on the resistance of the circuit and voltage across it.

(i)The impedance of the circuit is minimum  and equal to the resistance of the circuit.

From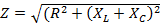   

When Z=Z_R, X_L = X_C

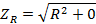
Z_R = R

 At series resonance

(ii)  The circuit current is maximum as it is limited by the resistance of the circuit alone.

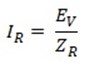
(iii)  Since at series resonance the current flowing in the circuit is very large, the voltage drops across L and C are also very large.

      In fact, these drops are much greater than the applied voltage.

    However, voltage drop across L – C combination as a whole will be zero because these drops are equal in magnitude but 180⁰ out of phase with each other.

RESONANCE CURVE

Resonance curve is the curve between the circuit current and the supply frequency.

 Figure below shows the resonance curve of a typical R-L-C series circuit.

Current reaches the maximum value at the resonant frequency f_o, falling off rapidly on either side at that point.

It is because if the frequency is below f_o, X_C > X_L and the net reactance is no longer zero.

Net reactance X

            X = X_C – X_L

If the frequency is above fo, then X_L > X_C and the net reactance is again not zero.

Net reactance X

X = X_L – X_C

In both cases, the circuit impedance will be more than the impedance Z_R at resonance.

The result is that magnitude of circuit current decreases rapidly as the frequency changes from the resonant frequency.

The effect of resistance in the circuit. The smaller the resistance, the greater is the current at resonance and sharper the resonance curve.

On other hand, the greater the resistance, the lower is the resonant peak.