SOLVED PROBLEMS
1. 1. Find the radius of the first orbit of hydrogen atom. What will be the velocity of electron in the first orbit? Hence find the size of hydrogen atom
Solution
The radius of nth orbit of it atom is given by
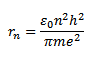
Radius of first orbit of it atom n=1
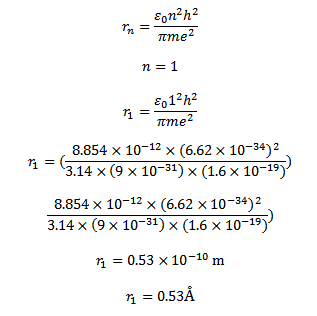
Velocity of electron in the nth orbit of hydrogen atom is given by
 =
= 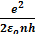
Velocity of electron in the first orbit of hydrogen atom is given by
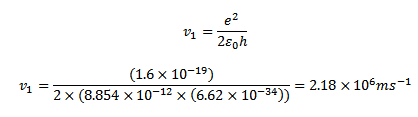
Since there is one electron in hydrogen atom the size hydrogen atom is equal to double the radius of the first orbit
Size of the atom
= 2
= 2 x 0.53Å
Size of an atom =1.06Å
2 2. (a) The hydrogen atom is stable in the ground, state why?
(b) The ionization energy of hydrogen is 13. 6eV what does it mean?
(c) Calculate the wavelength of second line of Lyman series
Solution
If the hydrogen atom is in the ground state (n=1) there is no state of lower energy to which a down ward transition can occur thus a hydrogen atom in the ground state is stable
a) It means that energy required to remove the single electron from the lowest energy state of hydrogen atom to becomes free electron is 13.6eV
b) Second line of Lyman series is obtained when electron jumps from third orbit 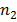 =3 to the first orbit n=1
=3 to the first orbit n=1
According to Bohr’s theory the wavelength of emitted radiation is given by
 =
=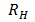
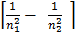
 =
= 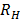
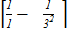
 =
=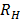 x
x 
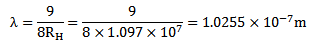
3 3.( a) What is the meaning of negative energy of orbiting electron?
(b) What would happen if the electron in atom were stationary?
Solution
a) The negative total energy means that it is bound to the nucleus. If it acquires enough energy from some external source (a collision for example) to make its total energy zero the electron is no longer bound it is free.
b) If the electrons were stationary they would fall into the nucleus due to electrostatic force of attraction so atom would be unstable i.e. it would not exist
c) For Paschen series we have longest wavelength line 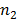 =4
=4
This is a wavelength in the infrared part. Other lines in this series have shorter wavelength bad approach series limit of wavelength to given by This wavelength is also in the hydrogen part. This the range or centre series (820.4nm to 1875nm) is the infrared
4. a) If an electron jumps from first orbit to third orbit will it absorb energy?
b) Name the series of hydrogen spectrum lying in the infrared region
c) Calculate the shortest wavelength of the Balmer series
d) What is the energy possessed by an electron for n=?
Solution
a) Yes it is because the energy level of third orbit is more than that of the first orbit
b) * Paschen series
* Bracket series
* P fund series
Solution
In Balmer series the radiation of shortest wavelength (i.e. of highest of highest energy) is emitted when electron jumps from infinity orbit 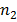 =
=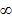 to the second orbit
to the second orbit 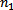 =2 of hydrogen atom.
=2 of hydrogen atom.
5 5. a) The ionization potential of hydrogen is 13.6V what does it mean?
b) Find the longest wavelength in Lyman series
c) How much is the ionization potential of hydrogen atom?
d) The energy of the hydrogen atom in the ground state is 13.6eV. Determine the energies of those energy levels whose quantum numbers are 2 and 3.
Solution
a) The ionization energy of hydrogen is 13.6eV. Therefore, if an electron which has been accelerated from rest through a p.d of 13.6V collides with a hydrogen atom it has exactly the right amount of energy to produce ionization.
This is a common method of producing ionization and therefore the term ionization potential is often used.
b) Solution
In Lyman series the radiation of longest wavelength (i.e. lowest energy) is emitted when electron jumps from second orbit 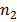 =2 to first orbit n=1 of hydrogen atom
=2 to first orbit n=1 of hydrogen atom
c) The energy of hydrogen atom in the ground state is – 13.6eV. therefore its ionization energy is 13.6eV and ionization potential =13.6V
d) Solution
The energy of an electron in the nth orbit of hydrogen atom is given by
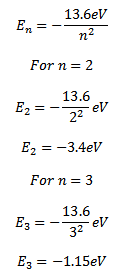
6
6. a) Name the series of hydrogen spectrum lying in the
i) Visible region
ii) Utraviolet region of electromagnetic spectrum
b) Write the empirical relation for Paschen series lines of hydrogen spectrum
c) What are the values of first and second excitation potential of hydrogen atom?
d) Calculate the radii and the energy of three lowest energy allowed orbits for the electron in Lithium ion. What is the energy of a photon that when absorbed causes an electron in Lithium ion to be excited from n=1 to n=3 state?
Solution
a) i) Balmer series
ii) Lyman series
b) The wavelength of the spectral lines in paschen series are given by
c) Excitation energy for first excited state = –3.4 – (-13.6)
=10.2eV
For second excited state
= – (1. 51 – (-13.6)
= 12.1eV
Solution
d) (I ) for a single electron atom or ion the radius of the nth orbit is given
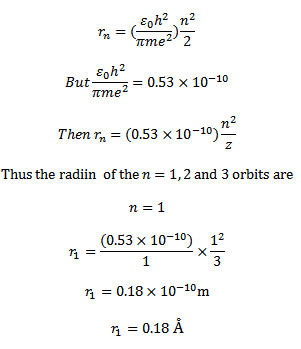
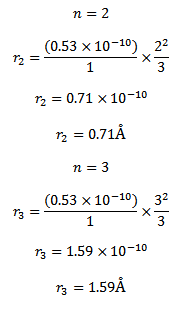
For a single electron atom or ion the energy of electron in the nth orbit is given by
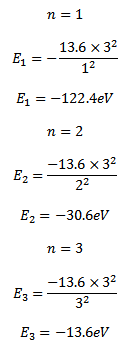
Thus the energy of n=1, 2 and 3 orbits. The photo energy must be equal to the energy needed to excite the electron
E3 – E1 =hf
(-13.6) – (-122.4) =photon’s energy
Photon’s energy = 108.8eV
7. The ionization energy of hydrogen like atom is 4rydbergs
(a) What is the wavelength of radiation emitted when electron jumps from first excited state to the ground state?
(b)What is the radius of the first orbit for this atom?
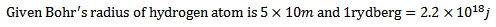
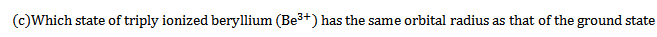
(d) According to Bohr’s theory what is the angular momentum of a electron in the third orbit
Solution
The energy electron in the nth orbit of hydrogen like atom is
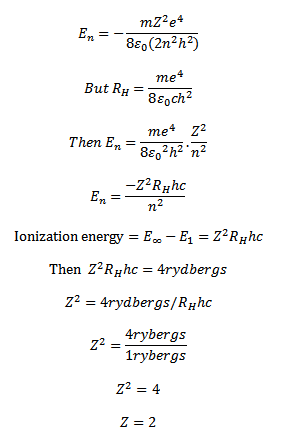
The energy required to excite the electron from n=1 level to n=2
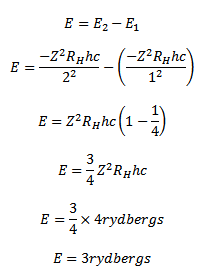
If is the wavelength of the emitted radiations then, Radius of first orbit for this atom
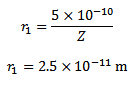
Solution
( b) Radius of nth orbit
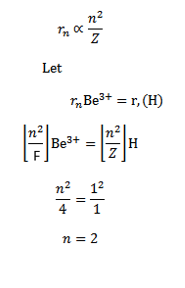

(c) Solution
Angular momentum L of an electron in nth orbit is
L = n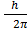
Here n=3
Then
L= 3 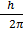
L=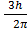
7 8. The energy levels of an atom are shown in figure below.
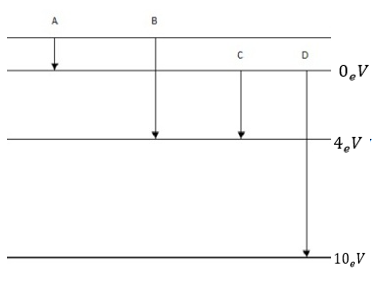
(a)Which one of these transitions will result in the emission of photon of wavelength 275nm?
(b) An electron orbiting in hydrogen atom has energy level of 3.4eV what will be its angular momentum
(c) The total energy of an electron in the first excited state of hydrogen atom is about
– 3. 4eV what is the wavelength?
solution
(a) Energy of emitted photon E
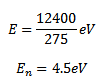
Therefore photon of wavelength 275nm will be emitted for transition B
Solution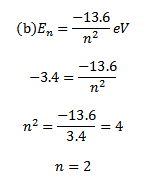
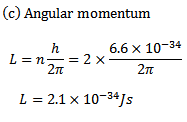
(d) K.E of electron = -(total energy of electron)
K.E of electron =3.4eV
ii) P.E of electron = 2xtotal energy
P.E of electron = -6.8eV
10. (a) How many lines can be drawn the energy level diagram of hydrogen atom?
(b) Use Bohr’s model to determine the ionization energy of the He ion also calculate the minimum wavelength a photo must have to cause ionization

(d) i) In neon atom the energies of the 3s and 3p states are respectively 16.70eV and 18.70eV. What wavelength corresponds to 3p -3s transitions in neon atom?
ii) The wavelength of the first member of the Balmer series in hydrogen spectrum is 6563Å. Calculate the wavelength of first member of Lyman series in the same spectrum
PLANCK’S QUANTUM THEORY OF BLACK BODY RADIATION
The findings in the black body radiation led Max plank in 1901 to postulate that radiant energy is quantized i.e. it is radiated in form of energy packets.
BASIC POSTULATES OF THE PLANK’S THEORY
1. Any radiation is associated with energy.
2. Radiant energy is emitted or absorbed in small packets known as quanta.
3. The energy associated with a quantum is proportional to the frequency f of the radiation
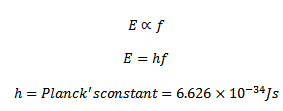
4. The energy is absorbed or emitted only in whole number of quanta
Black Body Radiation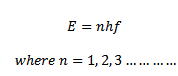
A blackbody is a substance that absorbs all light fall on it and does not reflect any light.
It is not easy to get a black body however a sealed metal box with a very small hole on it is very close to a black body.
From law of physics it follows that a good absorber of radiation also is a good radiator. A black body is supposed to be the best radiator.
When a black body is heated it emits light. The colour of light emitted changes from red to yellow then to white as the temperature is increased.
The change in colour with temperature shows that the frequency changes with temperature.
This in contradiction with the classical wave theory since in the classical wave theory energy is uniformly distributed over the wave form when heating the black body the colour of radiation should stay the same
Only the intensity is supposed to increase with temperature.
DISTRIBUTION OF ENERGY IN THE SPECTRUM OF A BLACK BODY
Lamer and Pringshein investigated the nglish-swahili/distribution” target=”_blank”>distribution of energy amongst the different wavelength of a thermal spectrum of a back body radiation
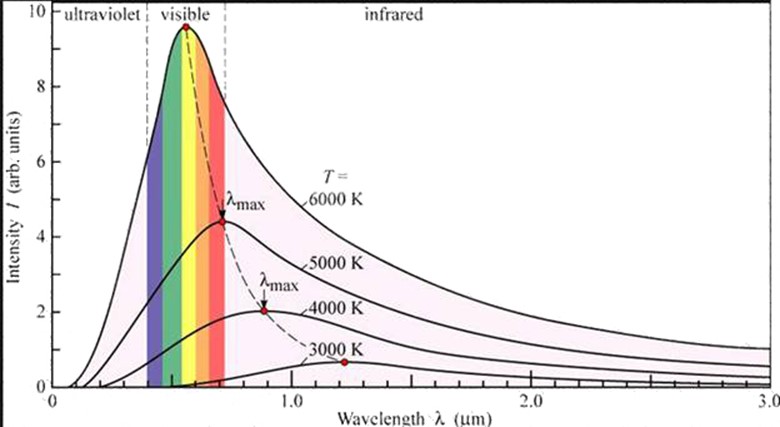
The results obtained by Lamer and Pringshein are shown in figure below
Results:
1. At a given temperature the energy is not uniformly distributed in the radiation spectrum of a hot body
2. At a given temperature the intensity of radiations increases with increased in wavelength and at a particular wavelength λ its value is maximum with further increase in wavelength the intensity of heat radiations decreased
3. With increase in temperature wave length increases, wavelength emission of energy takes place.
The points on the dotted line represent wavelength at various temperatures
4. For all wavelength an increase in temperature causes an increase in the energy emission The area under each curve represents the total energy emitted for the complete spectrum at a particular temperature
5. This area increases in temperature of the body. It is found that the area is directly proportional to fourth power of the temperature of the body
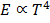
This represents Stefan’s Boltzmann’s law.
Plank’s constant
Plank’s constant is a fundamental constant equal to the ratio of the quantum energy to the frequency of the radiation.
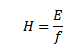
ELECTRON EMISSION
This is the liberation of electron from the surface of a substance.
For electron emission metals are used because they have many free electrons.
If a piece of metal is investigated at room temperature the random motion of free electrons is as shown in figure below
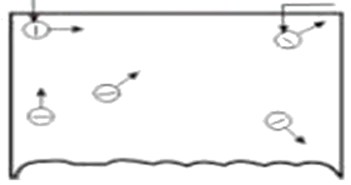
However these electrons are free only to the extent that they may transfer from one atom to another within the metal but they cannot leave the metal surface to provide electron emission.
It is because the free electron that start at the surface of metal find behind them positive nuclei pulling them back and none pulling forward.
This at the surface of a metal a free electron encounters force that prevents it to leave the metal
In other words the metallic surface offers a barrier to free electrons and is known as surface barriers
However if sufficient external energy is given to the free electron its kinetic energy is increased and thus electron will cross over the surface barrier to leave the metal.
WORK FUNCTION OF THE METAL
This is the additional energy required by an electron to overcome the surface barrier of the metal.
Or
This is the minimum energy required by an electron to just escape from the metal surface.
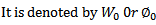

The work function depends on
i) Nature of metal
ii) Conditions of the metal surface
It is measured by a smaller unit of energy called electron volt. (eV) because this is the conventional unit of energy i.e. joule is very large for computations in atomic and nuclear physics.
Electron volt.
One electron volt is the amount of energy acquired by an electron when it is accelerated through a potential difference of IV
Since potential difference V
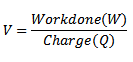
Work done = QV
For an electron
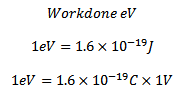
The electron volt is the kinetic energy gained by an electron being accelerated by a potential difference of one volt.
The work function of pure metal varies roughly from 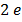 V to
V to 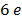 V as shown in table below
V as shown in table below
|
Metal |
Work Function Wo (eV) |
|
Cs |
2.14 |
|
K |
2.30 |
|
Na |
2.75 |
|
Ca |
3.20 |
|
Mo |
4.17 |
|
Pb |
4.25 |
|
Al |
4.28 |
|
Hg |
4.49 |
|
Cu |
4.65 |
|
Ag |
4.70 |
|
Ni |
5.15 |
|
Pt |
5.65 |
edu.uptymez.com
It is clear from the table above that the work function of platinum is the highest while it is lowest for Cesium.
It is desirable that metal used for electron emission should have low work function so that a small amount of energy is required to cause emission of electrons
PHOTOELECTRIC EFFECT
Photoelctric effect is the phenomenon of emission of electron from a metallic surface when radiation of suitable frequency falls on it or is the phenomenon where electromagnetic radiation of certain frequency when incident on certain material liberates electron from the surface of the material.
Photo emission
Photo emission is the emission of electron by electromagnetic radiation.
Photo electrons
These are emitted or rejected electrons from the surface of the cathode.
Photo electric effect is a general phenomenon exhibited by all substances but is most easily observed with metals.
When radiation of suitable frequency the threshold frequency is incident on a metallic surface electrons are emitted from the metal surface.
The threshold frequency is different for metals.
Certain alkali, metals e.g. sodium potassium, calcium show photo electric effect when visible light falls on them.
However, metal like zinc, calcium, magnesium etc show photo electric effect to ultra violet light.
Threshold Frequency
The threshold frequency is the minimum frequency of the incident radiation which is just sufficient to eject photo electron from surface of a metal Or is the minimum frequency of radiation below which no photo electron emission occurs.
It is denoted by 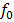
Illuminating a metal surface with light of frequency less than 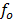 will not cause ejection of photo electrons, no matter now great is the intensity of radiation.
will not cause ejection of photo electrons, no matter now great is the intensity of radiation.
But illumination with a frequency greater than 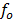 causes emission of photo electrons even if the radiation intensity is very small
causes emission of photo electrons even if the radiation intensity is very small
Threshold wavelength
The threshold wavelength is the maximum wavelength of the incident radiation at which photo electric emission occurs.

It is the wavelength corresponding to threshold frequency
If the wavelength of the incident radiation is greater than threshold wavelength then there will be no photo electric emission.
Photoelectric current is the photo-electrons emitted per second
EXPERIMENTAL STUDY OF PHOTO ELECTRIC EFFECT
Figure below shows the experimental set up for studying the photoelectric effect.

The arrangement consists of an evacuated glass or quartz tube inclusive a photosensitive cathode C and metallic A.
A transparent window W is sealed onto the glass tube which can be covered with different filters to obtain the desired frequency.
The anode and cathode are connected to a battery through a potential divided by which potential difference between anode and cathode can be changed.
The reversing switch RS tends to make anode positive or negative with respect to cathode.
The P.D between anode and cathode is measured by the voltmeter V while photoelectric current is indicated by the micro ammeter.
1.
1.Effect of intensity of light on photo electric current
The anode A is maintained at positive potential with respect to cathode C and a radiation of suitable frequency (above threshold frequency) is incident on cathode C.
As a result photo electric current is set up.
Keeping the frequency of incident radiation and accelerating potential fixed the intensity of the incident radiation is changed in steps.
For each value of intensity of radiations the corresponding value of photo electron current is noted.
If we plot a graph between intensity of radiation and photoelectric current it is found to be a straight line passing through the origin O as shown in figure below

This shows that photoelectric current is directly proportional to the intensity of incident radiation
The intensity of radiation can be changed by changing the distance between cathode C and the source of radiation.
Effect of potential of anode with respect to cathode on photoelectric current
We keep the anode at some positive accelerating potential with respect to cathode C and illuminate the cathode with radiation of fixed frequency f above threshold frequency and fixed intensity I
If we increase the positive potential on anode gradually, it is found that photo electric current also increases a stage comes when the photo electric current becomes maximum.
If we increase the positive potential on anode further the photo electric current does not increase.
This maximum value of photo electric current is called saturation current and corresponds to the photo electrons emitted by the cathode reach the anode A


Now saturation current is of higher value as shown in figure below
This is expected because the greater the intensity of incident radiation the greater is the photo electric current
Stopping potential
Stopping potential is the minimum retarding potential at which photoelectric current becomes zero Or is the potential difference when no electrons are able to reach the anode.
It is also known as stopping voltage or cut-off potential.

Stopping potential is a measure of the maximum kinetic energy of the photo electrons.
Since potential difference V
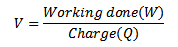
For stopping Voltage Vo

For an electron
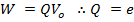
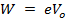
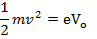
At V0, even the photo electrons having maximum kinetic energy K.E max (i.e. fastest photo electrons) cannot reach the anode A.
Therefore, the stopping potential V0 is a measure of the maximum kinetic energy K.E max of the photo electrons.
eV0 is the work done by the retarding force to stop the photo electron with maximum kinetic energy and is therefore equal to K.Emax.
At V0, it is found that the photoelectric current cannot be obtained even if we increase the intensity of radiation. It is same for different intensities I1, I2 and I3 of incident radiation.
3. Effect of frequency of incident radiation on stopping potential.
We now study the relation between the frequency f of the incident radiation and the stopping potential V0.
For this purpose, we take the radiations of different frequencies but of the same intensity.
For one frequency say f1, of the incident radiation, we plot the graph between photoelectric current and potential of anode A with respect to cathode C at a constant intensity of incident radiation
Keeping the intensity of incident radiation the same, we repeat the experiment for frequency f2 of the incident radiation.
The following is the resulting graph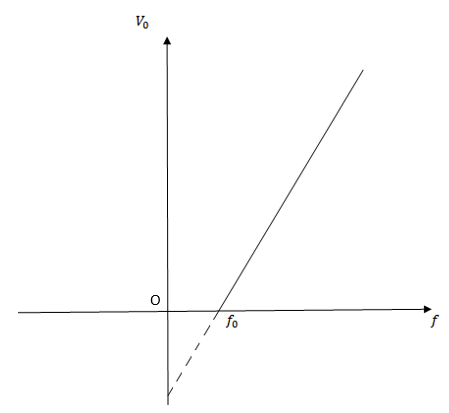
Observations from the graphs
1. The value of stopping potential is different from radiation of different frequencies
2. The value of stopping potential is move in low higher frequency. This implies that the value of maximum kinetic energy depend on the frequency of incident radiation.
The greater the frequency of incident radiation, the greater is the kinetic energy of emitted photo electrons.
3. The value of saturation current depends on the intensity of incident radiation but is independent of the frequency of incident radiation.
If we draw a graph between the frequency of incident radiation (f) and the stopping potential (V0) at constant intensity of radiation, it will be a straight line AB as shown in figure below
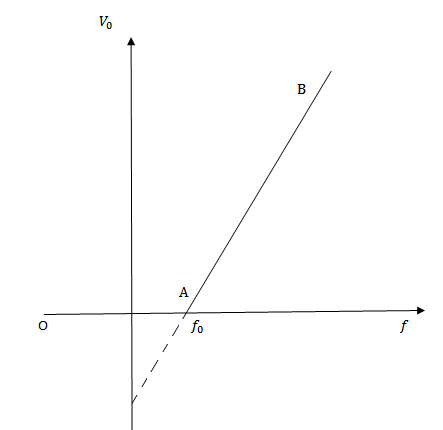
From the graph
At fo, stopping potential V0 = 0. It means that at fo, the photo electric current is just zero (i.e. photo electrons and emitted with zero velocity) and there is no retarding potential.
V0 = 0
This limiting frequency fo is called threshold frequency for the cathode material.
It is a minimum frequency of the incident radiation which is just sufficient to eject photo electrons (i.e. with zero velocity) from the surface of a metal.
Stopping potential is directly proportional to the frequency of incident radiation.
V0 α f
The greater the frequency of incident radiation, the higher is the stopping potential and vice versa.
Experiments show that photo electric emission is an instantaneous process.
As soon as light of suitable frequency (equal to or greater than fo) is incident on the surface of the metal, photo electrons are emitted from the metal surface.
The time delay is less than 10-9 second
LAWS OF PHOTOELECTRIC EMISSION
The above experimental study of photoelectric effect leads to the following laws of photoelectric emission.
i. For a given metal, there exists a certain minimum frequency of incident radiation below which no emission of photo-electrons takes place. This cut off frequency is called threshold frequency fo.
ii. For a given metal and frequency of incident radiation (>fo) the photo electric current is directly proportional to the intensity of incident radiation.
iii. Above the fo, the maximum kinetic energy of the emitted photo-electron is independent of the intensity of the incident radiation but depends only upon the frequency of the incident radiation.
iv. The photoelectric emission is an instantaneous process.
The above laws of photoelectric emission cannot be explained on the basis of light or radiation. This gave death blow to the wave theory of light or radiation.
FAILURE OF WAVE THEORY/CLASSICAL PHYSICS TO EXPLAIN PHOTOELECTRIC EFFECT
The wave theory of radiation failed to explain photoelectric effect. This will become clear from the following discussion.
I. According to wave theory of radiation the greater the intensity of the wave the greater the energy of the wave.
So wave theory does explain why the number of emitted photoelectrons increase as the intensity of radiation is increased.
But it fails to explain the experimentally observed fact that the velocity or kinetic energy of the emitted photoelectron is independent of the intensity of incident radiation.
According to the wave theory, an increasing in the intensity of radiation should increase the kinetic energy of the emitted photoelectrons but it is contrary to the experimentally observed fact.
II. According to wave theory, intensity of radiation is independent of it is frequency it depends upon the amplitude of electric field vector.
Therefore, an increase in the frequency of radiation should not affect the velocity or kinetic energy of the emitted electrons.
But it is observed experimentally that if the frequency of the incident radiation is increased, the kinetic energy of the emitted electrons also increases.
III. According to the wave theory, electrons should always be emitted from a metal by radiation of any frequency if the incident been is strong enough.
However experiments show that no matter how great is the intensity of the incident radiation; no electrons are emitted from the metallic surface if the frequency of radiation is less than a particular value i.e. threshold frequency.
IV. According to the wave theory the energy of radiation is spread continuously over the wave fronts of the radiation.
Therefore, a single electron in the metal will intercept only a small fraction of the wave’s energy.
Consequently considerable time should be needed for an electron to absorb enough energy from the wave to escape the metal surface.
But experiment show that electron are emitted as soon as radiation of suitable frequency falls on the metallic surface.
In other words photoelectric emission is instantaneous there is no delay.
The above discussion is a convincing proof of the inability of the wave theory to explain the photoelectric effect.
EINSTEIN QUANTUM THEORY OF LIGHT
Einstein explained photoelectric effect on the basis of Planck’s quantum theory.
According to Einstein light radiation consist of tiny packets of energy called quanta.
Photon
Photon is the single quantum of light radiation which travels with the speed of light.
The energy of a photon is given by E.
E=hf
where
f –frequency of light radiation
h – Plank’s constant.
Further, Einstein assumed that one photon of suitable frequency (=fo or >fo) can eject only one photoelectron from the metal surface.
He suggested that the energy of a single photon cannot be shared among the free electron in the metal.
Only one electron can absorb the energy of a single photon.
EINSTEIN’S PHOTOELECTRIC EQUATION
According to Einstein, one photoelectron is emitted from a metal surface if one photon of suitable frequency is incident on the metal.
Suppose a photon of suitable frequency f (< than the fo for the metal) is incident on the metal.
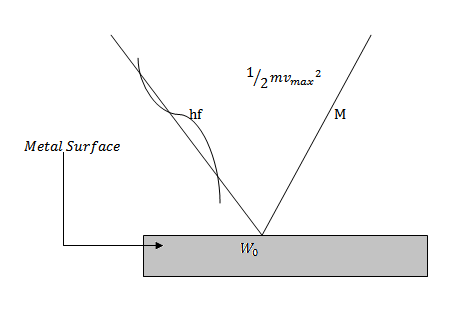
The energy hf of the photon is spent in two ways
I. A part of photon energy is used in liberating the least tight bound electron from the metal surface which is equal to the work function W0 of the metal.
II. The rest of the energy of photon appears as maximum kinetic energy of the emitted electron.
Einstein summarized this idea in what is called the Einstein photoelectric equation.
Photon = work function + maximum kinetic energy
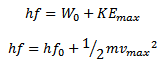
The above equation is known as Einstein’s photoelectric equation

If the frequency of the incident radiation is fo then the emitted photoelectron will have zero velocity.
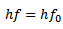
Maximum kinetic Energy of emitted photoelectrons is
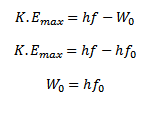
If f < fo, then from above equation K.Emax is negative which is impossible therefore, photoelectrons emission cannot occur if the frequency of incident radiation is less than fo.
If f > fo, then equation above K.Emax α f. This means that max kinetic energy of photoelectrons depends only on the frequency (f) of the incident radiation.
NUCLEAR PHYSICS
RADIOACTIVITY
This is the emission of radiations from heavily elements such as uranium whose nuclei are unstable.
Radiations emitted are called alpha 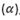 , Beta (β) particles and gamma
, Beta (β) particles and gamma 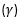 rays.
rays.
RATE OF DISINTEGRATION
The number of atoms of radioactive elements disintegrating per second 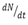 is directly proportional to the number of atom present at that instant.
is directly proportional to the number of atom present at that instant.
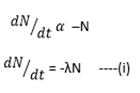
Where λ = decay constant
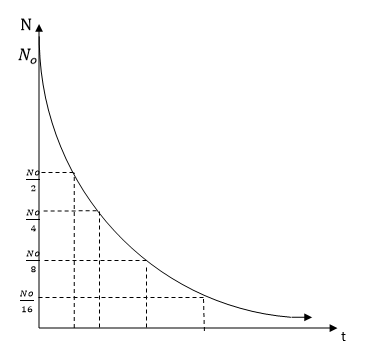
The negative sign (-) indicates that N decreases as time (t) increases.
If N0 is the number of atoms at time t= 0 and N is the number of atoms at time t. then:-
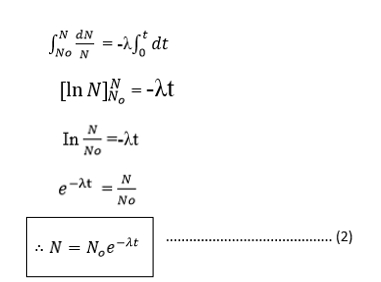
HALF LIFE
The half life time 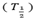 of a radioactive element is the times taken for the atoms disintegrate to half their initial number.
of a radioactive element is the times taken for the atoms disintegrate to half their initial number.
NECTA 1994/1/19
Draw a graph of 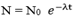
SOLUTION:
This is the graph of radioactive decay in time.

X-RAYS
X-rays are produced by bombarding a target of heavy metal with high energy electron.
NECTA 1984/2/8
The emission of X-rays may be regarded as the inverse of photo electric effect.Explain
SOLUTION
X-Rays which are waves are produced by bombarding a hard metal with electrons(particles)where as in photoelectric effect electron(particles) are liberated from ametal surface by incident radiation(waves)
MODERN X-RAY TUBE

Electron are obtained from the filament by thermionic emission and are accelerated to the anode having small target of high melting point such as tangstem.
X-RAY QUANTITY
Refers to the intensity of X-rays which increases with the number of electrons limiting the target.This depends on the cathode temperature controlled by the heating current
X-RAY QUALITY
Refer to the penetrating power of X-ray and determined by velocity whith which electrons strikes the target.
SOFT X-RAY:
Are those which can penetrate soft objects such as flesh
HARD X-RAY
Are those which can vibrate much more solid material
PROPERTIES OF X-RAY
1.They travel in a straight line.
2.They readily penetrate matter.
3.They affect photographic plates
4.They are not deflected by electric or magnetic field,because they have no charge
They are wave of wavelength 10A
X-RAY SPECTRA
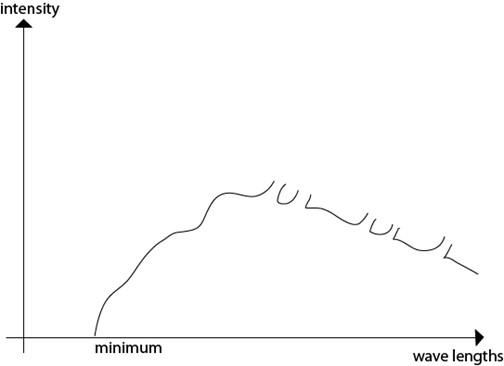
CONTINUOUS SPECTRUM
Explained by electromagnetic theory.
It is due to electrical interaction between the bombarding electrons and the nuclei of the target atom
An electron approaching a positively charged nucleus is accelerated and according to electromagnetic theory accelerated motion is accompanied by emission of radiations in this case x-ray
DISCRETE SPECTRA
These are explained by quantum theory.They are produced when the incident electron interact with electron close to nucleus of the target atom.The bombarding electrons knock off electron in their orbits and the created gaps are filled by electrons in the high energy levels,when they moves in these gaps they produce x-ray photon.
The cut off wavelength or short wave limit(λ min)
This is the minimum wavelength of x-radiations which corresponds to the maximum energy of the X-rays produced by electrons which have given out all their K.Æ on a single encounter with the target nucleus
ENERGY OF X – RAY:
Energy of an electron striking the atom of the target is eV where e = electronic charge.
V = p.d across the X-ray tube.
If a direct collision is made with a target atom and the energy is absorbed then on quantum theory X-rays produced hence a maximum energy hV
Therefore
eV = 1/2mV2 = hV
eV = hc/ λ minimum
λmin = hc/eV

NECTA 1989/1/18
Calculate the wavelength of most energetic X-rays produced by a tube operating at 1.0 x 105V.
USES OF X – RAYS
1.in investigation of suspected bone fractures
2.Detection of lung tuber culosis (feased tissue is denser than a heatthy one).
3.Treatment of cancer (cancer cells are killed by X-rays)
4.Casting and welding joints can be inspected for internal imperfection.
5.It is used in the study of crystal structure refer to Bragg’s law.
NUCLEAR FISSION FUSSION
Nuclear fission is a splitting disintegrating of heavy nucleus such as uranium into two other lighter nuclei (with several neutrons)
Example:

Nuclear fusion
This is the combination of light nuclei to form a heavier nucleus.
Example:

NECTA 1990/2/8
(1)Both fission and fusion are source of energy
Explain.
SOLUTION:
Fission-During disintegration of heavy nucleus such as uranium, energy is released which is
transformed into K.E of fragments.
Fussion-When light nuclei are fused together a large amount of energy is released in term of heat.(eg
in the sun)