An electric current is set up when a net charge Q passes through any section of the conductor in time t.
The charge assumed to be constant: i.e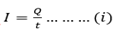 
If the value of the rate flow of charge is not constant the current varies with time and is given by the equation.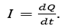
VELOCITY OF CURRENT CARRIES OR DRIFT VELOCITY (V).
The conduction of electricity in metal is due to free electrons. Free electron have the thermal energy and wonder randomly through the metal from atom to atom and hence collide.
The amplitude of vibration are then increased and the temperature of the metal rise.
On the average the electron drift in the direction of the drift in the mean velocity called drift velocity
Consider a metal wire of cross sectional area A and of length L.
Let “n” be the number of electrons per unit volume and “e” is the charge of an electron
The volume occupied by electron is AL
The total number of electrons is nAL
The total charge (Q) in the wire is nALe…….. (1)
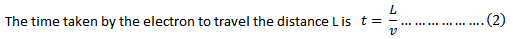
If I is the current flowing through this wire then,
I = Q/t ———————(3)
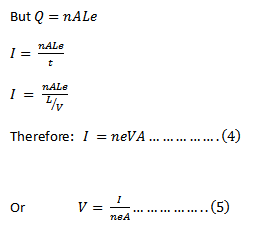
From equation 5
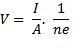
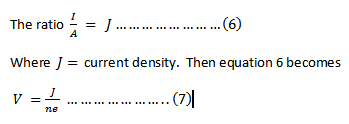
Examples
-
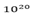Electrons each having a charge passing through point x towards a point y in 0.1 sec. What is the current and its direction?
edu.uptymez.com
2. A conductor with a cross section of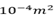 
and electric current of 1.2A. If the number of electrons be 
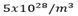calculate the electron velocity.(Take charge of an electron=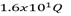
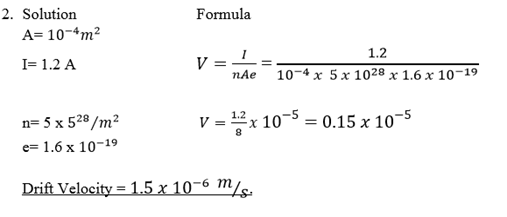
Q3 A uniform copper wire of diameter 0.051mm carries a current 10A. what is the drift velocity of electrons in the wire, assuming the charge of electrons is
1.6 X 10-19 C
RESISTANCE AND RESISTIVITY:
Ohm had shown that by using wires of different lengths and diameters.
Resistance of a wire R is proportional to its length
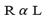
and inversely proportional to its cross section area. A i.e
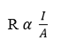
From (1) and (2) we have
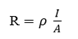
Where is the constant for the material of the wire and it is called. Resistivity.
The resistance of pure metal increases with temperature.
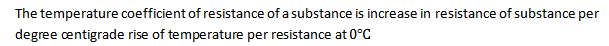
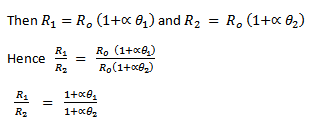
Example
A copper coil has a resistance of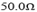 
at 
what its resistance at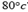 
?
Take the temperature coefficient of copper is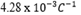 
Solution
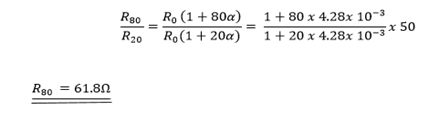
HEAT AND ELECTRICAL POWER
Consider an electrical device k and let potential difference between A and B be V.
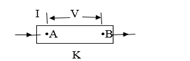
If Q is the charge passing through the ends in a time t then Q = It……….. (1)
Total energy given out by the conductor is W = VQ ………………(2)
Substitute eg (1) into eq (2) we get
W= VIt …… (3)
but workdone = electrical heat developed (H)
hence W= H =VIt …………(4)
Now V= IR so the eqn (4) becomes
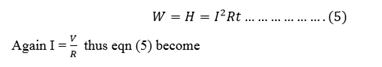
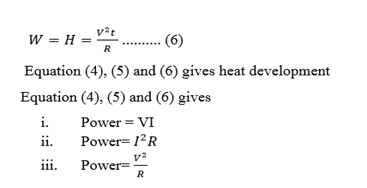
KIRCHHOFF’S LAWS
Some circuits cannot be broken down into set of series and parallel combination of conductors. It is then necessary to make use of generalized form of circuits laws already considered. These laws are known as Kirchhoff’s law
Kirchhoff’s first law:
The algebraic sum of current at any junction in the net work is zero
i.e. ∑ I = 0
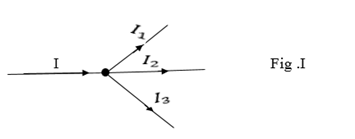
A current is given a positive sign if it flows towards a junction and negative sign if it flows away from the junction.
From figure I above we have
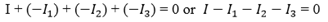
Kirchhoff’s second law:
The algebraic sum of emf’s around the loop is equal to the algebraic sum of all potential differences in that circuit i.e
