This is the production of a magnetic field by current flowing in a conductor.
The magnetic effect of current was discovered by Ousted in 1820. The verified magnetic effect of current by the following simple experiment.
Figure below shows a conducting wire AB Above a magnetic needle parallel to it.
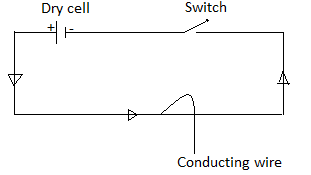
So long as there is no current in the wire, the magnetic needle remains parallel to the wire i.e. there is no deflection in the magnetic needle.
As soon as the current flows through the wire AB, the needle is deflected.
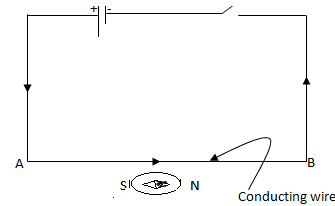
Magnetic needle
When the current in wire AB is Reversed the needle is deflected in the opposite direction
This Deflection is a convincing proof of the existence of a magnetic field around a current carrying conductor.
On increasing the current in the wire AB the deflection of the needle is increased and vice versa.
This shows that magnetic field strength increases with the increase in current and vice versa
It is clear from Worsted’s experiment that current carrying conductor produces a magnetic field around it.
The larger the value of current in the conductor the stronger is the magnetic field and vice versa.
Magnetic field
Is the region around a magnet where magnet effect can be experienced.
OR
Is the space around a current carrying conducting (magnet) where magnetic effects can be experienced.
The Direction of a field at a point is taken to be the direction in which a north magnetic pole would move more under the influence of field if it were placed at that point.
The magnetic field is represented by magnetic lines of force which form closed loops.
The magnetic field disappears as soon as the current is switched off or charges stop morning.
Magnetic flux Φ
is a measure of the number of magnetic field lines passing through the region.
The unit of magnetic flux is the Weber (Wb)
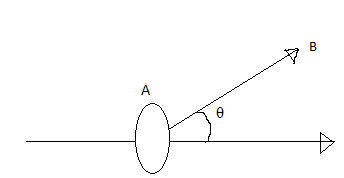
The flux through an area A on figure below the normal to which lies at angle 𜃠to a field of flux density B
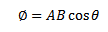
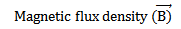
Is a quantity which measures the strength of the magnetic field
It is sometimes called magnetic
It is a vector quantity
The SI unit of Magnetic flux density is Tesla (T) or Wb/m2
Magnetic flux density is simply called magnetic field B
B = θ/A
FORCE ON A MOVING CHARGE IN A MAGNETIC FIELD
Consider a positive charge +Q moving in a uniform magnetic field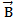 
with a velocity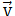 
Let the Angle between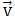 
and 
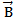be θ as shown
It has been found experimentally the magnetic field exerts a force F on the charge.
The magnitude F of this force depends on the following factors
(i) F α θ
(ii)F α B
(iii) 
Combining the factors we get
Where K is a constant of proportionality
The unit of B is so defined that K = 1
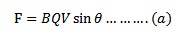
Equation (a) can be written in a vector form as:-
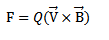
F = the force of the particle (N)
B = the magnitude of the magnetic flue density of the field T
Q = the charge on the particle
V= the magnitude of the velocity of the particle
Definition of 
From
F = BQVsinâ¡θ
If V = 1, Q = 1, θ= 90 then
F = Sin90
F=B
Magnetic field (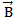 
) at a point in space is equal to the force experienced by a unit charge moving with a unit velocity perpendicular to the direction of magnetic field at that point
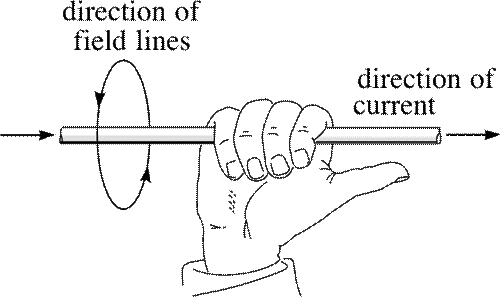
Right Hand Grip Rule
Grip the wire using the right hand with the thumb pointing in the direction of the current the other fingers unit point in the direction of the field.
– For an electron (negatively charged) entering the magnetic field as shown below
The Direction of positive charge will be exactly opposite. Applying Right hand Grip Rule it is clear that Direction of force on the electron will be vertically upward
For a positively charged particle, it will be vertically downward
Direction of magnetic field means from N –pole to S-pole.
SOME CASES OF MAGNETIC FORCE F
Consider an electric charge Q moving with a velocity V through a magnetic field B. then the magnetic force F on the charge is given by
F = BQV
(i) When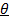 
= 0o or 1800
F = BQV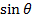
F= BQVSin00 or F = BQV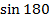
F= 0
Hence a charged particle moving parallel(or Anti parallel) to the direction of magnetic field experiences no force
(ii) When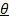 
=900
F = BQV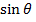
F = BQV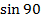
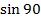=1
F = BQV
Hence a force experienced by charged particle is maximum when it is moving perpendicular to the direction of magnetic field.
(iii) When V=O, the charge particle is at rest.
F = BQV
F=BQ(0)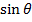
∴F=O
If a charged particle is at rest in a magnetic field it experiences no force.
(iv) When Q = O
F = BQV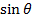
F = 0
Hence electrically neutral particle (eg neutron) moving in a magnetic field experiences no force.
The magnetic force F acts perpendicular to velocity V (as well as B)
This means that a uniform magnetic field can neither speed up nor slow down a moving charged particle; it can charge only the Direction of V and not magnitude of V
Since the magnitude of V does not charge the magnetic force does not change the kinetic energy of the charged particle.
UNITS AND DIMENSIONS OF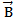 
The SI unit of magnetic field B is Tesla
Now
F = BQV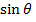
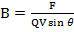
If Q = 1C, V =1m/s, Q= 900 F= 1N
B = 1T
Hence the strength of magnetic field at a point is 1T if a charge of 1C when moving with a velocity of 1m/s at right angles to the magnetic field, experiences a force of 1N at that points.
Magnetic field of earth at surface is about 10 – 4T. On the other hand, strong electromagnets can produce magnetic fields of the order of 2T.
Dimensions of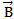 
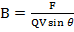
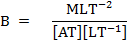
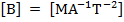
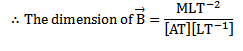
Worked Examples
1. A proton is moving northwards with a velocity of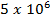 
m/s in a magnetic field of 0.1Tdirected eastwards. Find the force on the proton. Charge on proton = 1.6 x 10 -19C.
Solution
F = BQV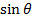
B= 0.1T
V=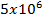 
m/s
F=0.1 X 1.6 X 10-19 X 5 X 106X Sin 90
Q = 1.6 X 10-19C
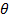= 900
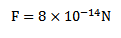
2. An electron experiences the greatest force as it travel at 3.9 x105 m/s in a magnetic field when it is moving westward. The force is upward and is of magnitude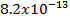 
N what is the magnitude and direction of the magnetic field.
Solution
The conditions of the problem suggest that the electron is moving at right angles
To the direction of the magnetic field
F = BQV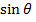
, F = 8.7 x 10 -13N
Q= 1.6 X10 -19C
V=3.9X105m/s
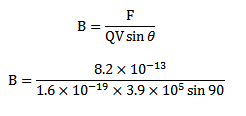
B = 13.14T
By right hand rule per cross product, the direction of the magnetic field is towards northward.
3. An α – particle of mass 6.65 x 10-27 kg is travelling at right angles to a magnetic field with a speed of 6×105m/s. The strength of the magnetic field is 0.2T.calculate the force on the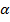 
– particle and its acceleration.
Solution
Force on α – particle F = BQV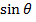
M = 6.65 X10-27Kg
V = 6 x 105m/s
B = 0.2T
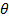= 900
F = BQV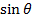
= (0.2 x 2x 1.6×10-19) x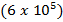 
x Sin90Ëš
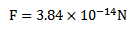
Acceleration of α – particle
F= mÉ’
É’= 
= 
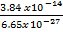
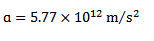
4. A copper wire has 1.0 x 1029 free electrons per cubic meter, a cross sectional area of 2mm2 and carries a current of 5A . The wire is placed at right angle to a uniform magnetic field of strength 0.15T. Calculate the force the acting on each electron.
Solution
I = neA
Drift velocity =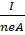 
n= 1×1029m-3 e = 1.6×10-19c A= 2mm2 = 2×10-6m2
I = 5A
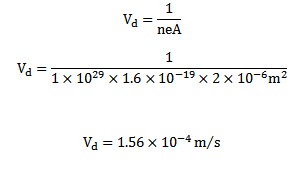
Force on each electron F= BQ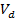
Sin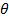
Q= 1.6 x 10-19c
B= 0.15T
Q=900
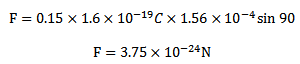
BIOT –SAVART LAW
The Biot – Savart law states that the magnitude of magnetic flux density dB at a point P which is at a distance r from a very short length dl of a conductor carrying a current I is given by.
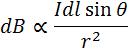
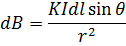
where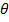 
is the Angle between the short length dl and the line joining it to point P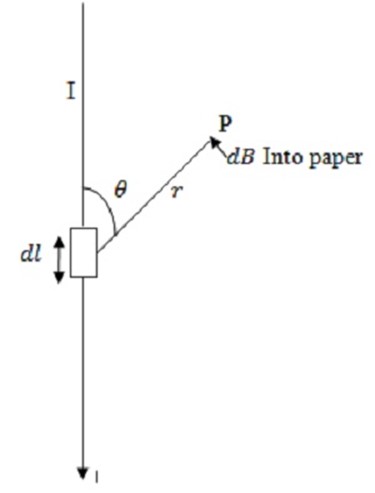
K is a constant of proportionality its value depends on the medium in which the conductor is situated and the system of units adopted.
For free space vacuum or air
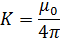
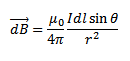
This equation is known as Biot –Savart Law and gives the magnitude of the magnetic field at a point due to small current element
Current element
Is the product of current (I) and length of very small segment (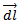
) of the current carrying conductor.
Current element =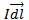
Current element produces magnetic field just as a stationary charge produces an electric field the current element is a vector.
Its Direction is Tangent to the element and acts in the direction of current flow in the conductor
Biot -Savart law holds strictly per steady currents
Direction of B
The direction of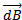 
is perpendicular to the plane containing 
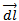and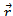 
by right hand rule for the cross product the field is directed inward.
Special cases
(i) When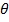 
= 00 or 1800
i.e Point P lies on the axis of the conductor
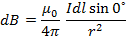
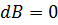
Hence there is no magnetic field at any point on the thin current carrying conductor minimum value.
(ii) When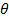 
= 900
When point P lies at a perpendicular position w .r. t current element
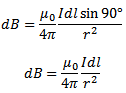
Hence magnetic field due to a current element is maximum in a plane passing through the element and perpendicular to its axis.
Important point about Biot – Savant law
(i) Biot – Savant law is valid per symmetrical current nglish-swahili/distribution” target=”_blank”>distributions.
(ii) Biot – Savant law cannot be proved experimentally because it is not possible to have a current carrying conductor of length dl
(iii) Like coulomb’s law in electrostatics, Biot- Savant law also obeys inverse square law
(iv) The Direction of dB is perpendicular to the plane containing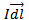 
and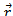 
(v) This law is also called Laplace’s law and inverse square law’
BIOT – SAVART LAW VERSUS COULOMB’S LAW IN ELECTROSTATICS
According to coulomb’s law in electrostatics, the eclectic field due to a charge element dQ at a distance r is given by
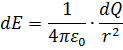
According to Biot – Savart law the magnetic field due to a current element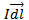 
at a distance r is given by
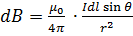
From the above two equations we note the following points of Similarities and Dissimilarities.
Similarities
(i) Both laws obey inverse square law
(ii) Both the fields(magnetic field and Electro static field) obey superposition principles
(iii)Both the fields are long range fields.
Dissimilarities
(i) The Electric field is produced by a scalar source i.e. Electric charge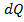
. However the magnetic field is product by a vector source i.e. current 
(ii) The Direction the Electric field is along the displacement vector i.e. The line joining the source and field point. However the direction of magnetic field is perpendicular to the plane containing current element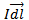 
and displacement vector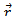 
(iii) In Biot –Savant law the magnitude of magnetic field dB α Sin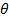
Where 
is the Angle between current element 
and displacement vector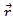 
However there is no angle dependence in coulomb’s law for electrostatics