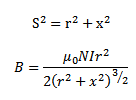MAGNETIC FIELD AT THE CENTER OF CURRENT CARRYING CIRCULAR COIL
Consider a circular coil of radius r and carrying current I in the Direction shown in figure
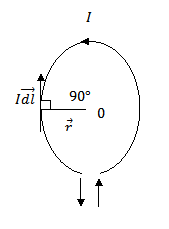
Suppose the loop lies in the plane of paper it is desired to find the magnetic field at the centre O of the coil
Suppose the entire circular coil is divided into a large number of current elements each of length 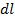
According to Biot – Savant law, the magnetic field 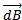 at the centre O of the coil due to current element
at the centre O of the coil due to current element 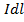 is given by
is given by
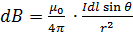 ……………
……………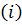
The direction of dB is perpendicular to the plane of the coil and is Directed inwards
Since each current element contributes to the magnetic field in the same direction, the total magnetic field B at the centre O can be found by integrating equation…………(i)
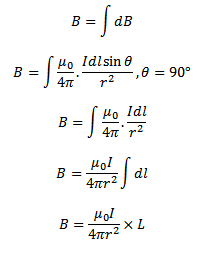
L- Total length of the coil = 2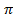 r
r
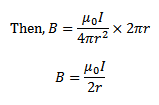
If the coil has N turns each carrying current in the same direction then contribution of all turn are added up.
B=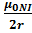
MAGNETIC FIELD DUE TO INFINITELY LONG CONDUCTOR
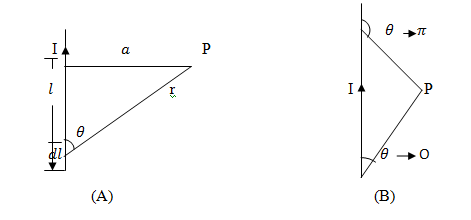
The flux density dB at P due to the start length dl given by equation as
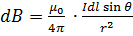
From the figure (A)
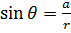 ,
, 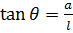
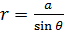
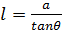
r = 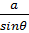
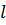 = a cot
= a cot 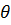
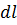 = -a
= -a
Substituting for 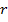 and
and  gives
gives

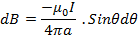
The total flux density B at P is the sum of the flux densities of all the short lengths and can be found by letting d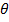 →O and integrating over the whole length of the conductor.
→O and integrating over the whole length of the conductor.
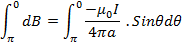
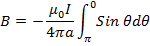
The limits of the integration are 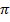 and 0 because these are values of 𜃠at the ends of the conductor
and 0 because these are values of 𜃠at the ends of the conductor
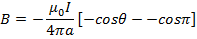
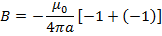

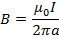
FLUX DENSITY AT ANY POINT ON THE AXIS OF A PLANE CIRCULAR
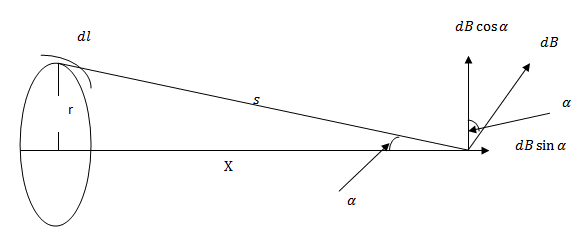

Circular coil with its plane perpendicular to that of the paper
The flux density dB at p due to the short length dl of the coil at X, where X is in the plane of the paper, is given by equation as
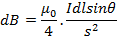
By symmetry, when all the short lengths 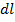 are taken into account the components of magnitude
are taken into account the components of magnitude  sum to zero.
sum to zero.
Each short length produces a component of magnitude 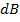 Sin α parallel to the axis and all those components are in the direction shown
Sin α parallel to the axis and all those components are in the direction shown
The total flux density is therefore in the direction of 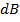 Sin α and its magnitude B is given by
Sin α and its magnitude B is given by
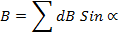
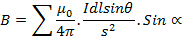
The radius vector XP of each small length is perpendicular to it, so that 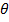 =900 and there pore Sin
=900 and there pore Sin = 1
= 1
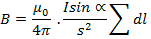
Since,
 = 2
= 2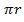 (the circumference of the coil)
(the circumference of the coil)
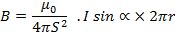
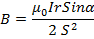 , But
, But 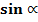 =
= 
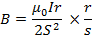
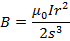
For a coil of N Turns
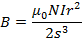
When S= r

Also from the figure