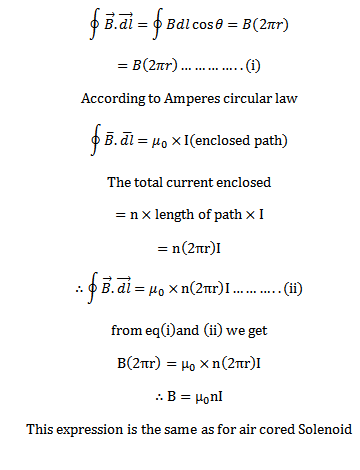AMPERE’S CIRCUITAL LAW
States that the line integral of magnetic field  around any closed path in vacuum/air is equal to
around any closed path in vacuum/air is equal to  times the total current (I) enclosed by that path
times the total current (I) enclosed by that path
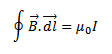

I = current enclosed by that path.
Ampere’s law is an alternative to Biot – Savart law but it is useful for calculating magnetic field only in situations with considerable symmetry.
This law is true for steady currents only.
In order to use law it is necessary to choose a path for which it is possible to determine the value of the line integral
It is because there are many situations where there is no such path that the law is of limited use.
Hence the application of ampere law
(i) Magnetic field due to constraining conductor carrying current
(ii)Magnetic field due to solenoid carrying current
(iii)Magnetic field due toroid
MAGNETIC FIELD DUE TO STRAIGHT CONDUCTOR CARRYING CURRENT
Consider a long straight conductor carrying current I in the direction as shown in the figure below
It is desired to find the magnetic field at a point p at a perpendicular distance r for the conductors
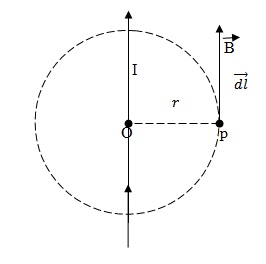
Applying Ampere’s circuital law to this closed path
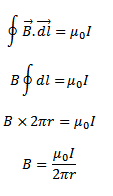
SOLENOID
Is a long coil of wire consisting of closely packed loops
Or
Is a cylindrical coil having many numbers of turns
By long solenoid we mean that the length of the Solenoid is very large as compared to its Diameter.
Figure below shows the magnetic field lines due to an air cored solenoid carrying current
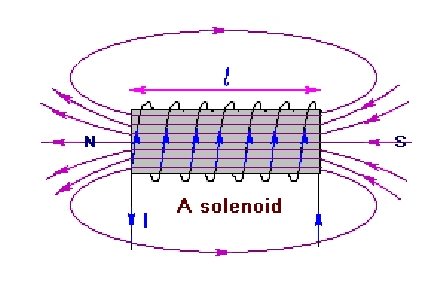
Inside the solenoid the magnetic field is uniform and parallel to the solenoid axis.
Outside solenoid the magnetic field is very small as compared to the field inside and may be assumed zero.
It is because the same no of field line that are concentrated inside the solenoid spread out into very faster space outside
Magnetic flux density due to an Axis of an in finely long Solenoid
Consider the magnetic flux density 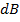 at P due to a section of the solenoid of length
at P due to a section of the solenoid of length 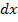
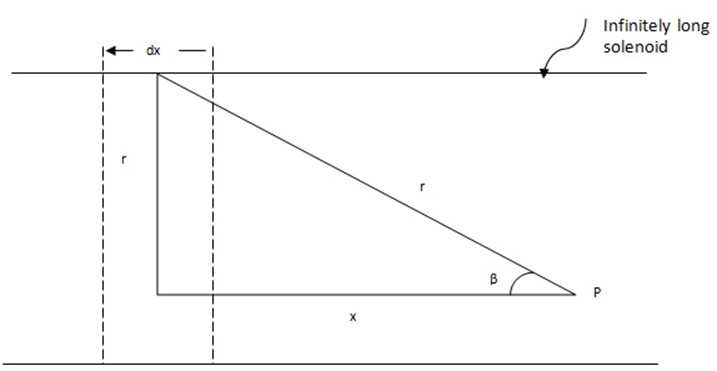
n = number of turns per unit length.
N= number of turns the section can be treated as a plane circular coil of N turns in which case dB is given by
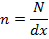
Since dx is small, the section can be treated as a plane circular coil or N turns in which case dB is given by
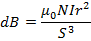
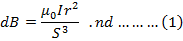
From the figure
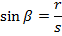
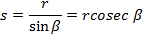
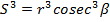
Also
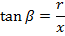
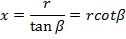
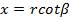
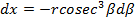
Substituting for 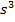 and dx gives,
and dx gives,
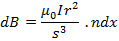
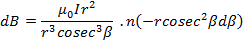
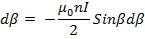

The flux densities at P due to every section of the Solenoid are all in the same direction and therefore the total flux density B can be found by letting dB→o and integrate over the whole length of the solenoid.
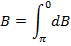
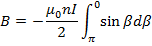
The limits of integration are  and 0 because these values of β at the end of the solenoid.
and 0 because these values of β at the end of the solenoid.

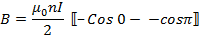
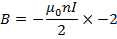
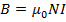
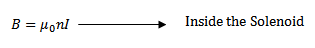
If the Solenoid is Iron-cored of relatively permeability 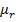 magnitude of magnetic field inside the Solenoid is
magnitude of magnetic field inside the Solenoid is
From
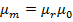
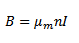
At points near the ends of an air cored Solenoid, the magnitude of magnetic field is

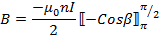

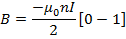
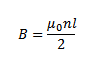
The magnetic field outside a solenoid is zero
Also in a current carrying long solenoid the magnetic field produced does not depend upon radius of the Solenoid.
TOROID
Toroid is a solenoid that bent into the form of the closed ring.
The magnitude field B has a constant magnitude every where inside the toroid while it is zero in the open space interior and exterior to the toroid.
If any closed path is inside the inner edge of the toroid then ther is no current enclosed. Therefore, by Ampere’s circular law B=0.
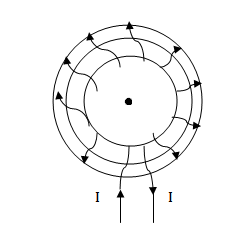
Magnetic field 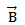 due to toroid
due to toroid
Consider the diagram below
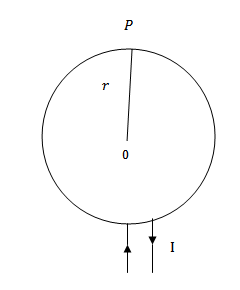
Let r = mean radius of toroid
I = Current through toroid
n = number of turns permit length
B = magnitude of magnetic field inside the toroid
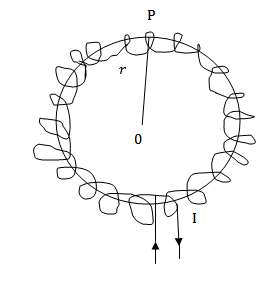
Then