FORCE ON A CURRENT CARRYING CONDUCTOR PLACED IN A MAGNETIC FIELD
We know that a moving charge in a magnetic field experiences a force
Now electric current in a conductor is due to the drifting of the force electrons in a definite direction in the conductor
When such a current carrying conductor is placed in a uniform magnetic field, each free electron experiences a force.
Since the free electrons are constrained in the conductor, the conductor itself experiences a force.
Hence a current carrying conductor placed in magnetic field experiences a force F.
Consider a conductor of the length L and area of cross- section a placed at an angle 𜃠to the direction of uniform of magnetic field B.
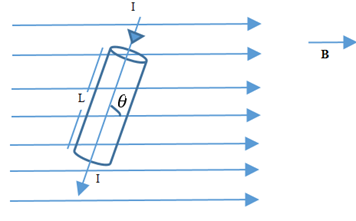
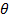– is the angle between the plane of the conductor. The magnetic force experienced by the moving charge in a conductor is F = BQV Sin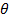
For steady current I = 
Q =I t
F=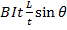 
The velocity for direct current is constant
V= 
F = B I t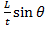
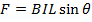
F= Force on the conductor (N)
B= Magnitude of the magnetic flux density of the field (T)
I = Current in the Conductor (A)
L= length of the conductor (M)
The current in the conductor I
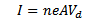
Special cases
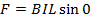
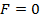
Thus if current carrying conductor is placed parallel to the direction of the magnetic field of the conductor will experience no force.
ii.)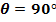 
F = BIL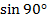
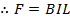
Hence current carrying conductor will experience maximum force when it placed at right angles to the direction of the field.
One Tesla
Is the magnetic flux density of a field in which a force of IN acts on a 1M length of a conductor which is carrying a current of IA and is perpendicular to the field.
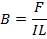
B = Tesla
The Direction of the force
Experiment shows that the force is always perpendicular to the plane which contains both the current and the external field at the site of the conductor
The direction of the force can be found by using Fleming’s left hand rule
Fleming’s left hand rule
States that if the first and the second fingers and the thumb of the left hand are placed comfortably at right angles to each other, with the first finger pointing in the direction of the current then thumb points in the direction of the force i.e. Direction in which Motion takes place If the conductor is free to move.
Maxwell’s Corkscrew rule
States that if a right handed corkscrew is turned so that its point travels along the direction, the direction of rotation of corkscrew gives the direction of the magnetic field.
FORCE BETWEEN TWO PARALLEL CONDUCTORS CARRYING CURRENTS
When two parallel current carrying conductors are close together, they exert force on each other.
It is because one current carrying conductor is placed in the magnetic field of the other
If currents are in the same direction the conductor attract each other and If currents are in the opposite directions conductors repel each other
Thus like currents attract, unlike currents repel.
Consider two infinitely long straight parallel conductors X and Y carrying currents I1 and I2 respectively in the same direction.
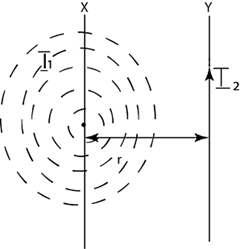
Suppose the conductors are separated by a distance rin the plane of the paper.
As each conductor is in the magnetic field produced by the other, therefore each conductor experiences a force
The current carrying conductor Y is placed in the magnetic field produced by conductor X
Therefore force act on the conductor Y. The magnitude of the magnetic field at any point P on the conductor Y due to current I, in the conductor X is
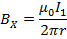
By right hand grip rule ; the direction of B is perpendicular to the place of the paper and is directed inwards.
Now conductor Y carrying current 
is placed in the magnetic field 
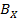produced by conductor X
Therefore force per unit length of conductor Y will experience a force 
given by
= 
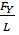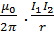
According to FLHR, force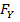 
on conductor Y acts in the place of the paper perpendicular to Y and is directed towards to the conductor X.
Similarly, the Force on conductor X per unit length is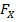 
= ByI1L
But
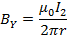
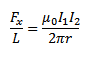
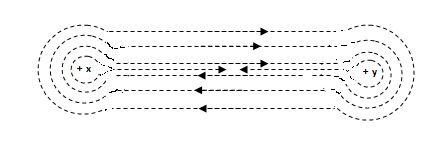
Hence when two long parallel conductors carry currents in the same direction they attract each other. The force of attraction per unit length is
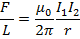
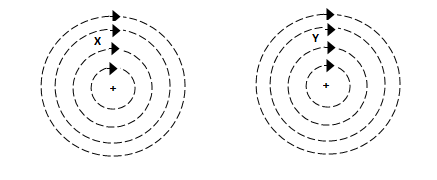
This shows that the attraction between two parallel straight conductors carrying currents in the same direction in terms of magnetic field lines of conductors
It is clear that in the space between X and Y the two fields are in opposition and hence they tend to cancel each other
However in the space outside X and Y the two fields assist each other. Hence resultant field nglish-swahili/distribution” target=”_blank”>distribution will be
If two straight current carrying conductors of unequal length are held parallel to each other then force on the long conductor is due to the magnetic field of the short conductor
I1 = Current through short conductor
l = Length of short conductor
I2 = Current through long conductor
L = Length of long conductor
If r is the separation distance between these parallel conductors
Force on Long conductor = force on short conductor
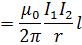
Force on each conductor is the same in magnitude but opposite in direction (Newton’s third law)
DEFINITION OF AMPERE
Force between two current currying conductors per unit length
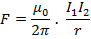
If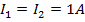 
And r =1m then
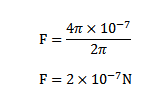
Ampere
Is that steady current which when it is flowing in each of two infinitely long, straight parallel conductors which have negligible areas of cross – section and are 1m apart in a vacuum, causes each conducts to exert a force of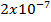 
N on each mete of the other.
WORKED EXAMPLES
1. The plane of a circular coil is horizontal it has 20 turns each of 8cm radius A current of 1A flows through it which appears to be clockwise from a point vertically above it. Find the Magnitude of the magnetic field at the centre of the coil.
Solution
The magnitude of the magnetic field at the centre of the coil carrying current is given by,
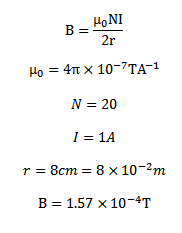
As the currents appears to be clockwise from appoint vertically above the coil the direction of the field will be vertically downward (By R.H.G.R)
2. A wire placed along the South-North direction carries currents of 5A from South to North. Find the magnetic field due to a 1cm piece of wire at a point 200cm North-East from the place.
Solution
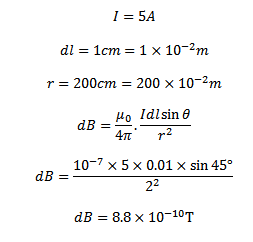
By RHGR, The field is vertically vertical downwards
3. A coil of radius 10cm and having 20 turns carries a current of 12A in a clockwise direction when seen from east. The coil is in North – South plane. Find the magnetic field at the centre of the coil.
Solution
The magnitude of the magnetic field at the centre of the coil
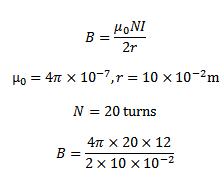
The electron of hydrogen atom moves along a circular path of radius 0.5 x 10-10 with the uniform speed of 4 x 106 m/s. Calculate the magnetic field produced by electron at the centre ( e= 1.6 x 10-9c)
Number the revolution made by the electron in 1 second is
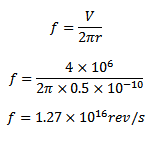
Current =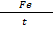 
I = 1.27 X 1016 X 1.6 X10-19
1S
I = 2.04 X 10-3A
Magnetic field produced by the electron at the centre is
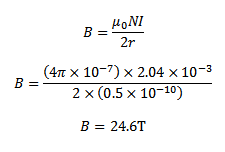
5. A circular coil of 100 turns has a radius of 10cm and carries a current of 5A Determine the magnetic field
(i) At the centre of the coil
(ii) At a point on the axis of the coil at a distance of 5cm from the centre of the coil.
Solution
(i) Magnetic field at the centre of the coil is
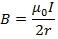
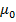= 4
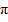x 10-7 TA -1
N = 100 turns
I = 5A
r = 10×10-2m
B = 4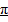
x 10-7x 100 x S
2 X 0.1
B= 3.14 X10-3 T
The magnetic field of the centre of the coil = 3.14 X10-3 T
(ii) Magnetic field on the axis of the coil at a distance X from the centre is
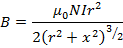
= 4
x 10-7 TA -1
N = 100 turns
I = 5A
r = 10 x 10-2
x = 0.05m
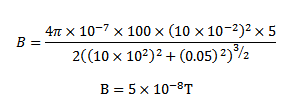
6. An electric current I is flowing in a circular wire of radius at what dose from the centre on the axis of circular wire will the magnetic field be 1/8th of its value at the centre?
Solution
Magnetic field B at the centre of the circular coil is
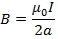
Suppose at a distance X from the centre on the axis of the circular coil the magnetic field is 
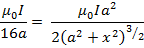
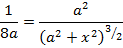
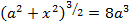
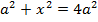
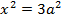
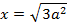
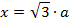
7. In Bohr’s model of hydrogen atom the electron circulates around nucleus on a path of radius 0.51Å at a frequency of 6.8x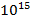
is rev/second calculate the magnetic field induction at the centre of the orbit.
Solution
The circulating electron is equivalent to circular current loop carrying current I given by
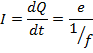
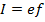
I = 1.6 
I = 1.1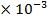
A
Magnetic field at the centre due to this current is
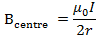
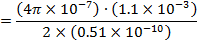
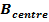= 14T
8. A long straight wire carries a current of 50A. An electron moving at 107ms is 5cm from the wire
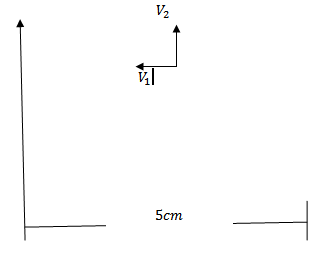
Find the Magnetic field acting on the electron velocity is directed
(i) Towards the wire
(ii) Parallel to the wire
(iii) Perpendicular to the directions defined by I and ii
Solution
The magnetic field produced by current carrying long wire at a distance r
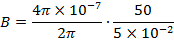
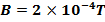
The field is directed downward perpendicular to the plane of the paper
( i) The velocity V1
is towards the wire. The angle between VI and B is 900 force on electron
F= BQV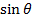
F = 2x 10-4 x 1.6×10-19x107x Sin 900
F = 3.2 x 10-16 N
(ii) When the electron is moving is moving parallel to the wire ,angle between V2 and B is again 90Ëš Therefore, force is again
3.2×10-16N
(iii) When the electron is moving perpendicular to the directions defined by (i) and (ii) the angle between V and B is O
F = O
9. A solenoid has a length of 1 .23 m and inner diameter 4cm it has five layers of windings of 850 turns each and carries a current of 5.57A. what is the magnitude of the magnetic field at the centre of the solenoid
Solution
The magnitude of the magnetic field at the centre of a solenoid is given by
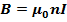
But
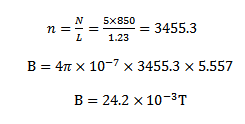
10. A to void has a core ( non – ferromagnetic) of inner radius 20cm and over radius 25cm around which 1500 turns of a wire are wound. If current in the wire is 2A
Calculate the magnetic field
(i) Inside the to void
(ii) Outside the to void
Solution — go to next page…