NUMERICAL
PROBLEMS
1. (1)The magnetic moment of a magnet (10cm x 2cm x 1cm) is 1AM? What is the intensity of magnetization?
I = 5 X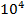 
A/m
2. (2)An iron rod of cross sectional area 4
is placed with its length parallel to a magnetic flied of intensity 1600 A/M the flux through the rod is 4 x 10-4Wb what is the permeability of the material of the rod?
μ = 0.625 x10-3 Wb A -1 m-1
3. (3) A toroid winding carrying a current of 5A is wound with 300turns/miter of core. The core is Iron which has a magnetic permeability of 5000Mo under the given conditions
Find (i) the magnetic intensity H
(ii) Flux density B
(iii) Intensity of magnetization I
i) 1500AT/m
ii) 9.43T
iii) 7.5 X106A/m
4. (4)A specimen of Iron is uniformly magnetized by a magnetizing field of 500 A/m. if magnetic induction in the specimen is 0.2Wb/m2, find the relative permeability and susceptibility
Xm = 317.5
Mr = 318.5
5. Consider a toroid of 1000 turns and mean radius 25cm. what is the B- field in the toroid if there is a current of 2A?
What will be the field when the toroid is filled with Iron per which μ = 100H/m?
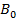= 1 .6 x 10 -3
B = 0.16T
6. An Iron of volume 10-4m3 and relative permeability 1000 is placed inside a long solenoid wound with storms/cm. if a current of 0.5A is passed through the solenoid, find the magnetic moment of the rod.
M = 25Am2
7. The flux through a certain toroid clangs from 0.65m Wb to 0.91M Wb when Air core is replaced by another material. What are
i) The relative permeability
ii) Absolute permeability of the material
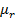= 1. 4
μ= 5.6 x10-7H/m
8. Answer the following Questions
a) Why does a paramagnetic sample display greater magnetization (per the same magnetizing field) when cooled?
b) Why is diamagnetism, in contrast almost independent of temperature?
c) Distinguish between a soft and a hard magnetic material, giving an example of soft magnetic materials are those which can easily be magnetized but do not retain their magnetism (retentively )
An example of soft magnetic material
Is soft Iron i.e. Iron in a reasonably pure state. It is otherwise known as wrought iron
Hard magnetic material
Are those which are difficultly to magnetic but once magnetized, can retain the magnetism per long
These are usually used making permanent magnetic
An example of hand magnetic material is steel which consists of iron and a small % of carbon
MOTION OF CHARGED PARTICLE IN UNFORM MAGNETIC FILED
Consider a charged particle of charge +Q and mass M moving with a velocity V in the plane of the paper.
Suppose this charged particle enters a uniform magnetic filed B which is perpendicular to the plane of the paper and directed outward
Clearly the entry of the charged particle is at right angles to the magnetic field
The force i.e. magnetic force Fm on the charged particle is given by
Fm = BQV
The magnetic force Fm acts at right angle to the plane containing V and B
On entering the magnetic field at M the charged particle experiences a force of magnitude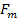 
and is deflected in the direction shown
This force is at right angle to the direction of motion of the charge particle and therefore, cannot change the speed of charge particle it only charge its direction of motion
A moment later, then the particle reaches point N the magnitude of force Fm acting on it is the same as it was at M but the direction of force is different (Fm is still perpendicular to V )
Thus the force is perpendicular to the direction of motion of the charged particle at all times and has a constant magnitude
The magnetic force does not change the speed or kinetic energy of the charge particle it only charges the direction of the charged particle
When the moving charged particle is inside the uniform magnetic field, it moves along a circular path.
When the initial velocity of the particle is parallel to the magnetic field
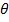= 00
From
Fm = BQV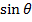
Fm = BQV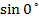
Fm = 0
Thus in this case the magnetic field does not exert any force on the charge particle
Therefore the charged particle will continue to move parallel to the magnetic field then 
= 1800
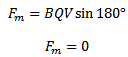
Therefore, the particle will continue to the move in the original direction.
When the initial velocity of the particle is perpendicular to the magnetic field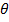 
=900
From
Fm = BQV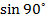
Max. Value Fm = BQV
PARAMETERS OF MOTION
A force of constant magnitude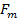 
always acts perpendicular to the direction of motion of the charged particle.
Therefore ,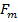 
provides the necessary centripetal force 
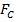to more the charged particle in a circular path in the circle of radius r perpendicular to the field
i) RADIUS OF PATH
The acceleration of a particle moving along a circular path of radius r is given by
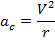
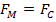
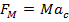
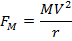
For a given charge mass and magnetic field r 
V. this means that fast particles move in large circles and slow ones in small circles.
ii) TIME PERIOD
The time taken by the charged particle to complete one circular revolution in the magnetic field is its Time period T
From
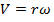
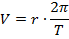
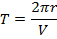
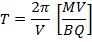
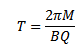
Thus Time period of the charged particle is independent of the speed (V) and the radius of the path
It only Depends on the magnitude of B and charge to mass ratio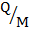 
of the particle .
FREQUENCY
The number of circular revolutions made by the charged particle in one second is its frequency f
f = 
f = 1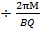
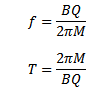
There Frequency of the charged particle is also independent of speed (V) and radius (r) of the path
ANGULAR
FREQUENCY
From
=2πf
But
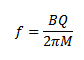
Then
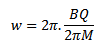
Again Angular frequency of the charged particle is independent of the speed (V) and radius (r) of the path..
Since T, f and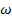 
of a charged particle moving in a magnetic field are independent of its speed (V) and the radius (r) of the path.
In fact all the charged particles with same Q/M and moving in a uniform magnetic field B will have the same value of T, f and w