FORM 6 PHYSICS: ELECTROMAGNETISM PART 5

ELECTROMAGNETIC MOMENT(M)
This is the magnetic torque acting on the coil when it is parallel to a uniform field whose flux density is one tesla.It is the property of the coil is defined as the couple required to hold the coil at right angles to
field.

         Thus, in equation τ=m when B=1I

from 

    

                                                                                                             

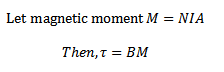
Consider a rectangular coil ABCD placed at an angle  to the magnetic field of flux density B

 

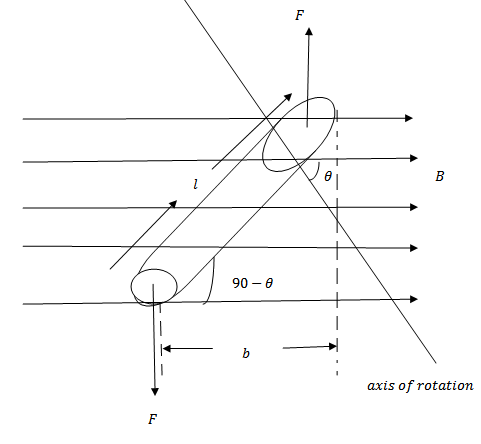
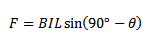
The perpendicular distance between the parallel force is 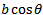 and not b.  Then the magnetic force or compile is given

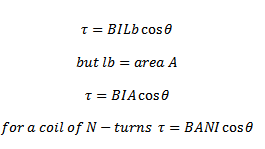
Special cases

(i)                     When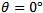   

              Plane of the loop is parallel to the direction of magnetic field

 

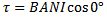
Thus,  the  Torque  on a  current  loop  is  maximum  when  the  plane  of the  loop is  parallel to the  direction of  magnetic field is given by

(ii)                   when 𝜃 = 90⁰

Plane of the loop is perpendicular to the direction of magnetic field

                      

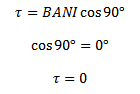
  Thus , the  torque on a current loop is  minimum (zero)  when  the  plane  of the  loop is  perpendicular

(iii)                 When  B = 1T

when B = 1T, then the magnetic torque is numerical equal to magnetic moment

From

 

 B = 1T

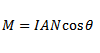
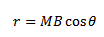
        MAGNETIC TORQUE AT AN ANGLE α BETWEEN THE AXIS OF THE COIL AND NORMAL TO THE PLANE OF THE COIL

We can also express torque in another useful form. If  normal to the  plane  of  coil  makes an  angle  α with  the  direction of the magnetic  field

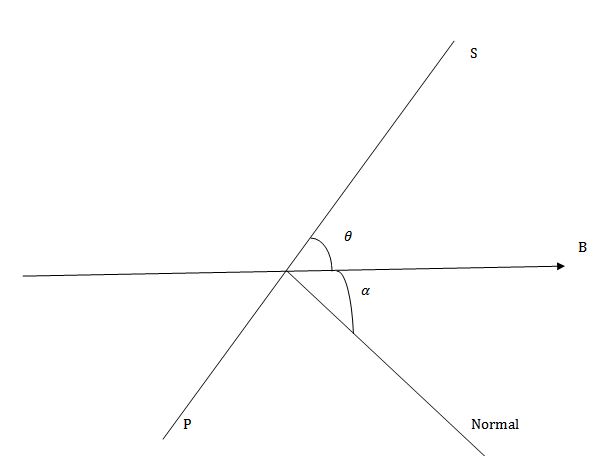
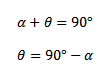
From

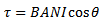
τ = BANI cos (90 – α)

τ = ANIBSin α                  

Since M = IAN

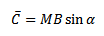
When  a  current carrying coil is  placed  in a  uniform magnetic field, torque acts on it  which tends to  rotate the  coil so that  the  plane of the  coil is  perpendicular   to the  direction of  magnetic field.

WORK DONE BY TORQUE
If the magnetic torque displaces the coil through the small angular displacement

The work done by the torque is given by

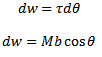
The total work done is obtained by integration the above equation within limits

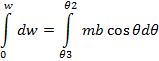
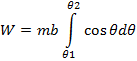
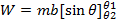
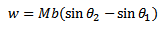
 If the  magnetic  field  displaces the  coil through small angular displacement 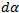 the  work done by  torque is  given  by 

dw = τdα

dw = mbSinαdα

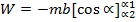
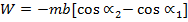
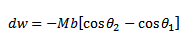
 WORKED EXAMPLES
1.       A vertical rectangular coil of sides 5cm by 2cm has 10 turns and carries a current of 2A. Calculate the torque on the coil when it is placed in a uniform horizontal magnetic field of 0.1T with its plane.

(a)      Parallel to the field

(b)      Perpendicular to the field

(c)      60⁰  to the field

Solution

The area of the coil

A= (5 x 10 ^-2) x (2 x10^-2)

A= 10^-3 m²  

(a)      From

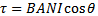
A=10^-3

I = 2A

N=10

B=0.1T

                    τ= 0.1 X10^-3 X10 X2

                         τ = 2 X10^-3NM

(b)

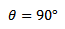
                          τ=BANI

                            τ= 0

(c)

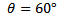
τ = BANICos 𝜃

τ= 0.1 x10^-3 x10x2xCos 60⁰

τ= 10 ^-3NM

2.      2.Given  a  uniform magnetic  field  of  100T in East  to West direction and a 44cm long  wire  with  a  current  carrying capacity  of  at most  10A. what  is the  shape and  orientation  of the  loop made  of  this wire  which yields maximum turning effect  on the  loop?

Solution

 A  current  carrying  planar loop will experience  maximum together  if  its  area to the  direction of the  magnetic  field  for a given  perimeter , a  circle has  the  maximum area.

If 44cm wire is bent into a circular

      2πr = 44

      πr = 22

      22r = 22

        7

      r = 1

      7 

      R = 7cm

Area of loop = πr²

                        = πx7²

                      = 154cm²
=      154×10^-4m²

Magnetic toque τ

                                   

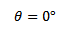
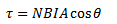
                                   τ = BANI

                                   τ = (154 X10^-4) X 100 X100

                                   τ = 150 T

 3. A circular coil of wire of 50 turns and radius 0.05 carries current of 1A the wire is suspended vertically in a uniform magnetic field of 1.5T. the  direction of magnetic field  is  parallel to the  plane  of the  coil

(a)      Calculate  the  Toque  on  the  coil

(b)      Would  your answer  charged  if the  circular coil is  replaced  by a plane  coil of  some  irregular  shape that  has  the  same  area (all other  particulars  are  unaltered? )

(a)       Solution

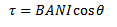
B = 1.5T

A = πr² = π (0.05) M²

A = 7.85 X 10^-3

N = 50

I = 1A

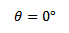
τ = 1.5 X (7.85 X10^-3) X50X1

τ = 0.589NM

(b)       Since torque on  the  loop is  independent  of  its  shape provide  area  (A) remains the  same  the  magnitude  of the  torque will remain  unaltered.

4.       A  circular  coil  of  20turns  and  radius 10 cm  is  placed  in a  uniform magnetic  field  of  0.2T normal to  the  coil. If current in the coil is 5A find.

(i)        Total  torque  on the  coil

(ii)       Total force  on the  coil

⁽ⁱⁱⁱ⁾      Average force on each electron in the coil due to the magnetic field. The coil is made of copper wire of cross-sectional area 10^-5m² and  force of electron  density in the  wire  is  10²⁹m^-3

Solution

(i)                    The  toque on the  coil is  given  by

     

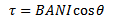
         Since

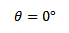
         τ = 0

(ii)     The  net  force  on a planar  current  loop in a  uniform magnetic field  is  always  zero

(iii)     Magnetic  force  on each electron

         F = BeV_d

         F = Be.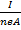

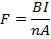
F =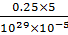 

F= 10^-24N