FORM 6 PHYSICS: ELECTROMAGNETISM PART 6

LAWS OF ELECTROMAGNETIC INDUCTION
While the magnitude of the induced EMF is given by Faraday law. Its direction can be predicted by Lenz’s Law
LENZ’S LAW
The direction of induced 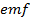is such that it tends to oppose the flux change which causing it and does oppose it if induced current flows

Faraday or Newman’s  laws
The induced is directly proportional to the rate of change of the flux through the the coil.
If E = induced then

NOTE
I). The minus sign express Lenz’s Law
II). Nɸ is the flux linkage in the coil

INDUCED EMF IN A MOVING ROD

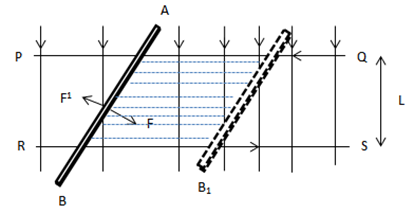
Area swept in 1 second

AB is a wire which can be moved by a force F in a contact with a smooth metal rails PQ and RS. A magnetic field of flux density B acts downwards perpendicular to the plane of the system.
As the wire AB cuts the flux density the 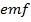is produced by the current I and is in opposition to the motion

Therefore

F= BIL ……………………………………………………..i
Where l is the distance between two rails

And    I = 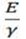  ……………………………………………………………ii
Where 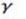  is the resistance of the wire
If the wire is moving with a speed V then  F’ = F  ……………….iii

F’ = 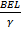……………………………4

Power = = =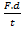 Force x velocity

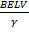= ……………………… 5

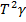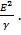
Also power = = = 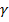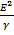…………….6

Equating equation 5 and 6

=

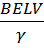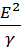
I.e. E = BLV (This is the induced 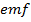in a moving coil)

INDUCED EMF IN A ROTATING COIL

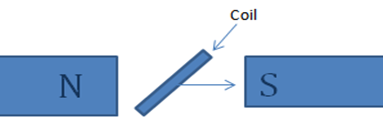
Consider a coil of an area A and its normal makes an angle of 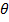with the magnetic field B_Y

The flux linkage with the coil of n turns is expressed as

N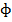 = 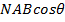………………………………………………………1

The induced emf is given by

E = = – = =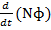
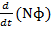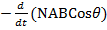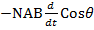
E = since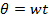

If the maximum value of emf is denoted by _o

Then

E = E_o sinwt where E_o = NABw

A gain w =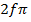

Therefore

1.     

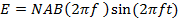
2.      E_o =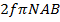

Exercise 1

The magnetic flux Q_B through the loop perpendicular to the plane of the coil and directed into the paper as shown in the diagram is varying according to the equation Q_B = 8t² +5t +5 where Q_B is measured in millimebers and t in seconds

i.                    What is the magnitude of induced 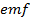in the loop when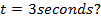

ii.                  What is the direction of the current through R?

Solution

E =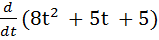

E = 16t + 5

E = 53Mv

Exercise 2

What is the maximum 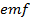induced in a coil of 500turns, each with an area of 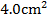, which makes 50reflections per second in a uniform magnetic field of flux density 0.04T?

Solution

B = 0.04T

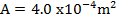
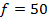
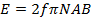
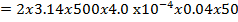
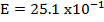
2.5Volts

INDUCED EMF IN ROTATING DISC – DYNAMO

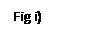
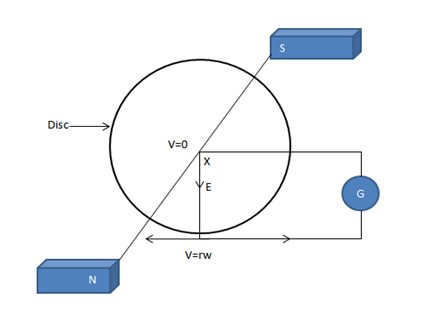
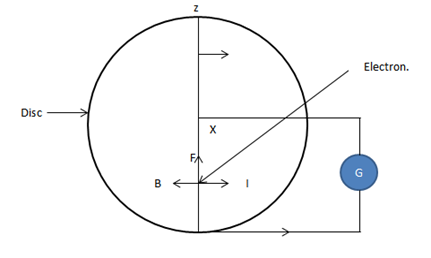
Consider a copper disc which rotates between poles of magnets. Connections are made to its circle and the circumference. An induced emf is obtained between the Centre of the disc and one edge. We assume that magnetic field is uniform over the radius xy

The radius 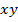continuously cuts the magnetic flux between the poles of the magnet. For this straight conductor, the velocity at the end of x is zero and that at the other end y 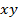where w is the angular velocity of the disk

Average velocity of 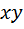is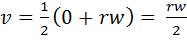

An induced 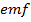in straight conductor is given by

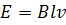In this case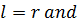

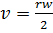
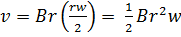^{…………………………………………………….i)}

Since 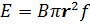…………………………………………ii)

If the disc has the radius r₁ and an axle at the Centre of radius r₂ the area swept out by a rotating radius of the metal disc is 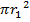– 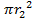= 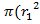– in this case the induced 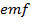would be

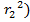–f

The direction of the E is given by Fleming’s right hand rule

As the disc rotates clockwise the radius 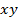moves to the left at the same time as the radius 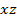moves to right

If the magnetic field covers the whole disk, induced 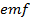in the two radii would be in opposite direction. So the resultant emf between yz would be zero. 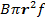The emf between the Centre and the rim of the disc is the maximum 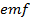which can be obtained

Qn.

A circular metal disc with a radius of 10cm rotates at 10revolutions per seconds. If the disc is in a uniform magnetic field of 0.02T at a right angle to the plane of the disc. What will be the 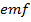induced between the Centre and the rim of the disc?

Solution

B = 0.02T

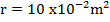
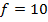
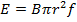
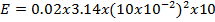
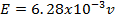
SELF INDUCTANCE (L)

An induced emf appear in the coil if the current in that coil is changed is called self-induction and 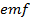produced is called self-induced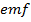

For a given coil produced no magnetic materials nearly the flux linkage 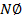proportional to the current I

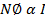Or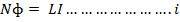

Where L is a constant proportionality which is called self-inductance of a coil

From Faraday’s law in such a coil 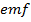the induced

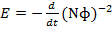
Substitute i) in ii)

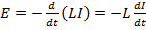or

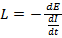
Hence the unit of inductance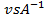. A special name the Henry has been given to this combination of units

Two coils A and B have 200 and 800turns respectively. A current 2Amperes in A produces a magnetic flux of 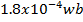in each turn of A, compute:

i.                    Mutual inductance

ii.                  Magnetic flux through A when there is a current of 4.0 Ampere in B

iii.                The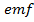 induced when the current in A changes 3A to 1A in 0.2seconds