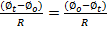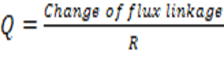SELF INDUCTANCE (L) FOR THE COIL
The induced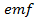
, 
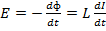
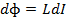(By integrating the equation we have)
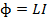
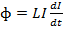
Therefore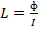 
The self-inductance may be defined as the flux linkage per unit current, when 
is in wabers and I is in amperes then L is in henry:
Magnetic flux density for a long coil is given by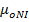 
with an iron core with a relative permeability of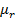
The flux density is given by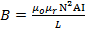 
since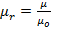 
Thus the flux linkage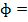 
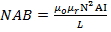
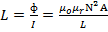(Unit for L is Henry)
ENERGY STORED IN AN INDUCTOR
Because of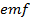 
of the self-induction that act when the current in the coil change, electrical energy must be supplied in setting up the current against the 
.
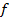If L is the self-inductance of the inductor then the back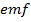 
across it is given by
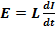…………………………i)
Hence rate at which work is done against the backward emf.
Power = EI…………………………ii)
Substitute equation i) into ii)
Then equation ii) becomes
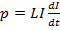
The work done to bring the current from zero to a steady state value Io is
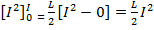
Therefore
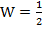
MUTUAL INDUCTANCE (M)
The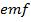 
may be induced by in one circuit by changing current in another. This phenomenon is often called mutual induction and the pairs of circuits which shows it are said to have mutual inductance
The mutual inductance m between the two circuits is defined by the following equation
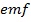Induced in B by changing = M (rate of change of current in A) i.e.
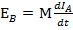
The unit of mutual inductance is Henry the same as that of self-inductance
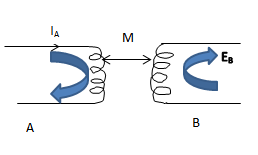
MUTUAL INDUCTION
Since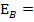 
the rate of change in flux in B then
QUANTITY OF ELECTRICITY INDUCED
Consider a close circuit of total resistance R Ohms which has a total flux linkage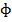 
with magnetic field B. if the flux linkage starts to change
Induced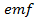
, 
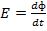but current
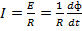
Flux linkage will not change at a steady rate and a current will not be constant. But throughout it changes. Its charge is being carried round the circuit. If a time t seconds is taken to reach a new constant value the charge carried round the circuit in that time is
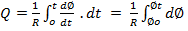
Where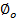 
is the number of linkage at t=o and 
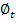is the number of linkage time t
Thus 
