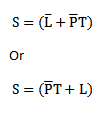LOGIC GATES
SYMBOL
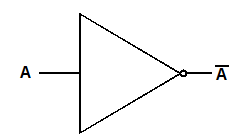
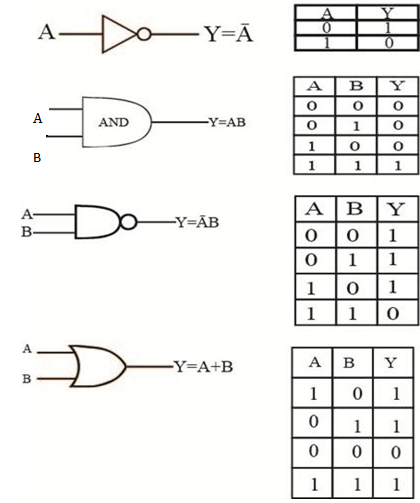
i. NOT GATE(INVERTER)
 he
he
It has only one input and one output.

ii. OR GATE
This can have many number of inputs but only one input. It gives high output if either of the inputs is high or all inputs are high.
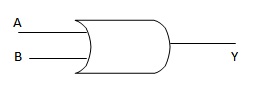
TRUTH TABLE FOR OR GATE

iii. AND GATE
It can have many number of inputs but only only one output. It gives high output when both input are high.
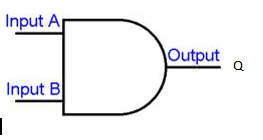
TRUTH TABLE FOR AND GATE
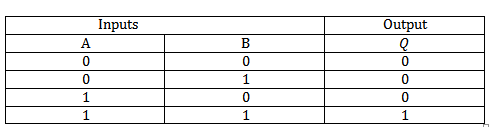
iv. NOR GATE
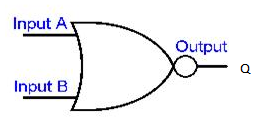
This is equivalent to OR gate followed by NOT gate.All outputs of OR gate are inverted
TRUTH TABLE FOR NOR GATE
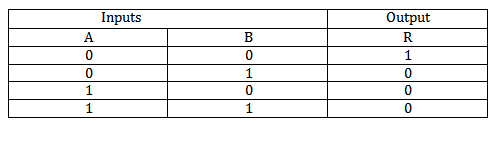
v. NAND GATE
This is the AND gate followed by NOT gate . This is widely used gate . In this case the outputs of AND gate re inverted.
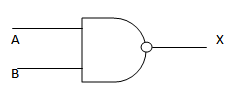
TRUTH TABLE FOR NAND GATE

All logic gates described can be connected together to form different function
(i)They are used to control traffic light
(ii)They are used in communication system
(iii)They are used in arithmetic and data processing
Questions
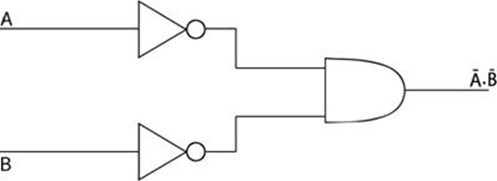
1. Find the expression for Y and form the truth table of the following diagram.
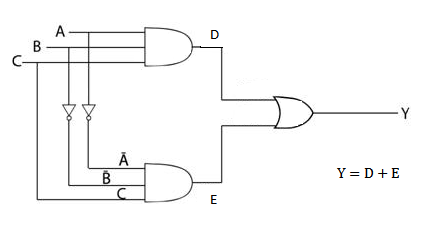
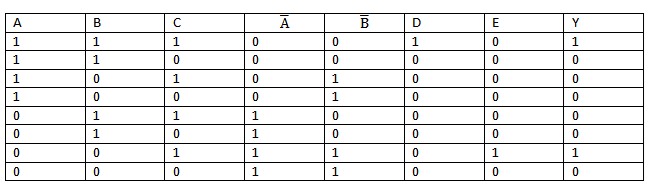
Solution
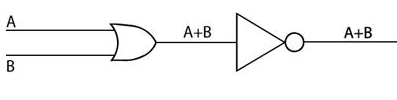
2. From the logic circuit below form the Boolean expression and draw the truth table
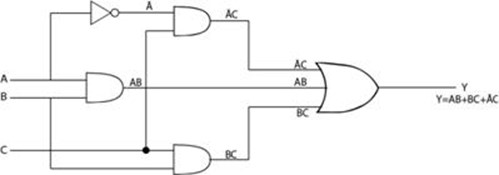
Solution
| Truth Table | |||
| A | B | C | Y |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
edu.uptymez.com
Laws of Boolean algebra
T1: Commutative law
a) A+B=B+A
b) AB=BA
T2: Associative law
a) (A+B) +C=A+ (B+C)
b) (AB) C=A (BC)
T3: Distributive law
a) A (B+C) =AB+AC
b) A+BC= (A+B) (A+C)
T4: Identity law
a) A+A+=A
b) AA=A
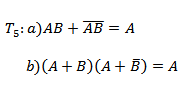
T6: Redundancy law
a) A+AB=A
b) A (A+B) =A
T7: a) 0+A=A
b) 0A=0
T8: a) I+A=I
b) 1A=A
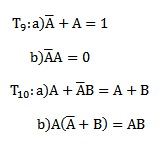
T11: De Morgan’s theorem
Example
1) Prove that
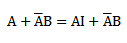
Algebraically
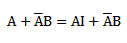
=A (I+B) +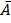 B
B
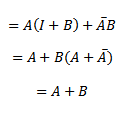
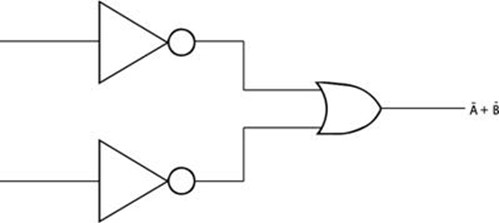
Question
For a lift (L), these are the conditions:
i) The lift door must be closed giving d=1
ii) The appropriate floor button (B) must be pressed B
L= Bd but not L=B+ d
A boiler shut down solenoid (s) will operate if the temperature T reaches 50 and the circulating pump P ise turned off or if the pilot light L goes out.