A fraction is a number that can be written in the form of 
Where a and b are intergers and b 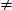 0
0
The number which is written on top of fraction is called Numerator and the bottom is called denominator e.g
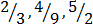
Type of fraction
(i) Proper fractions
– A proper fraction is the one in which the numerator is less than denominator
e.g. 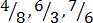 etc
etc
(ii) Improper fractions
– These are the ones which the numerators are greater than the denominator
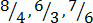 etc
etc
(iii) Mixed fractions or mixed numbers
– These are the ones formed after improper fractions are divided complete
e.g. 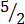 = 2
= 2 , 6
, 6 , 9
, 9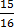
(iv) Equivalent fractions
These are two or more fractions that can be simplified to equal lowest fraction.
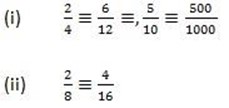
Example: Change the following into mixed numbers
1. 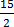 = 7
= 7
2. 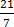 = 3
= 3
3. 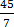 = 6
= 6
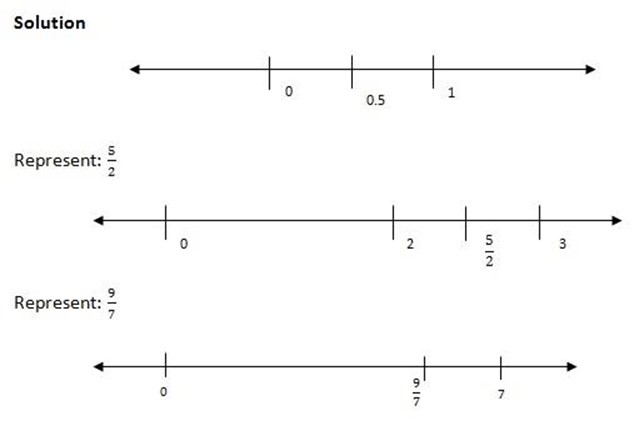
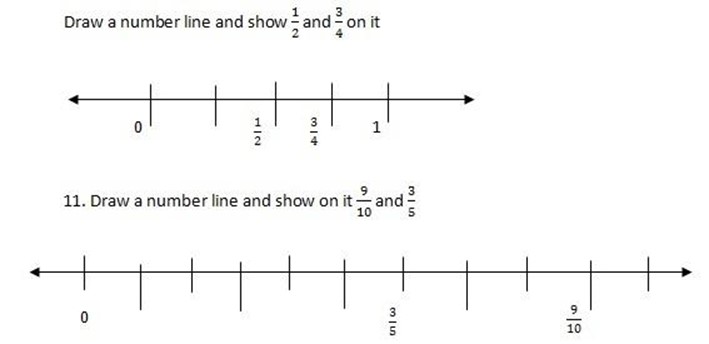
Fractions can be represented on number lines
e.g. represent 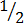 on a number line.
on a number line.
Exercise 1
1. (i)Which of the following are: –
(a) Proper fractions
(b) Mixed fractions
(c) Improper fractions
(ii) List four equivalent fractions
(i) 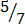
(ii) 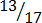
(iii) 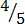
(iv) 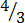
(v) 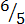
(vi) 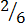
(vii) 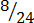
(viii) 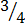
(ix) 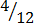
(x) 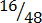
(xi) 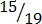
(xii) 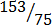
(xiii) 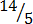
(xiv) 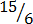
(xv) 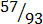
(xvi) 3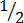
Solution
(a) Proper fraction
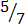 ,
, 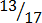 ,
, 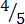 ,
, 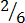 ,
, 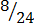 ,
, 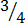 ,
, 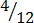 ,
, 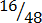 ,
, 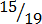 ,
, 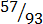
(b) Improper fraction
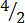 ,
, 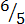 ,
, 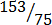 ,
, 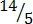 ,
, 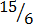
(c) Mixed fraction
1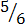 , 3
, 3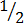
Four equivalent fractions are:-
1. 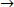
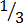

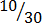 ,
, 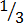

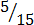
2. 
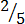

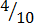 ,
, 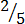

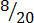
3. 
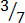

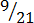 ,
, 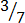

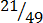
4. 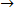
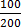

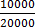 ,
, 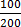

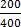
2. Write the following fractions in words
(a) 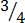
 three quarters
three quarters
(b) 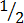
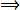 A half
A half
(c) 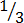
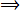 A third
A third
(d) 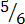
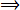 Five over six
Five over six
(e) 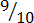
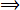 Nine over Ten
Nine over Ten
(f) 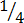
 A quarter
A quarter
2. Write the name of the fraction of the shaded part in figures ABCD and EFGH
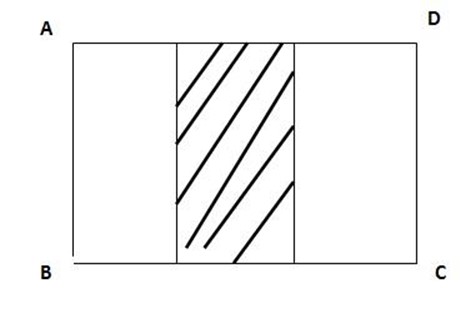

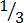 = one over three (A third)
= one over three (A third)
Which is a proper fraction
E H

F G

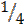 = one over four (A quarter)
= one over four (A quarter)
Which is a proper fraction
Comparison of fraction
Fraction can be compared by using two methods
(i) Number line
(ii) L.C.M of the denominators
(I) Number line
Example 1. show 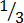 and
and 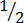 on a number line and then find which is greater than the other
on a number line and then find which is greater than the other


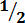
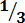
Example 2. Which is greater between 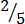 and
and 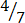 ?
?
Solution:
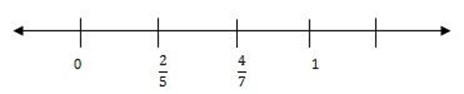

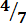
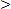
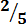
(II) L.C.M of the denominators
Determine which fraction is greater between 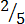 and
and 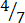
Solution
1st find the L.C.M of 5 and 7
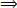 L. C. M of 5 and 7 = 35
L. C. M of 5 and 7 = 35
2nd multiply by that L. C. M each fraction
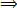

 35 = 14
35 = 14
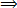

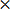 35 = 20
35 = 20
Conclusion, check the one which has given us bigger number after multiplication with L.C.M

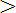

Example: which is greater  or
or 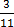 ?
?
Solution:
L.C.M = 44


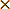 44
44
=99

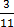
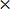 44
44
=12
:- 
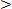
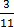
Operations on Fractions
Addition and Subtraction of Fraction
NOTE:
1 .Add the numerator together if each fraction has the same denominator.
2. If the fraction has different denominator, you must find the smallest number that each denominator divides into exactly. (LCM)
3. When adding fractions, do not add the denominator.
Example:
Evaluate the following fractions
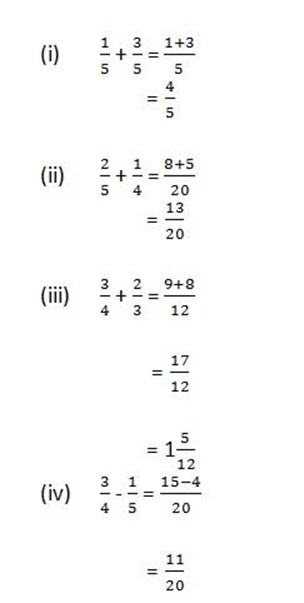
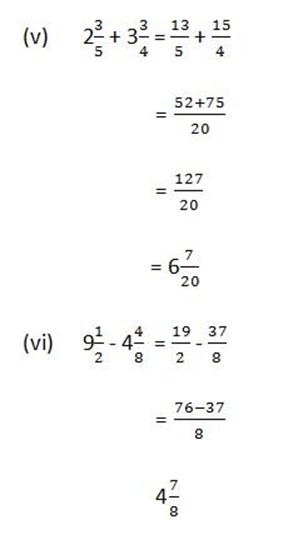
Multiplication
NOTE: 1. Before multiplying a number convert mixed number into improper fractions
2. Multiply the numerators and multiply the denominator.
Examples:
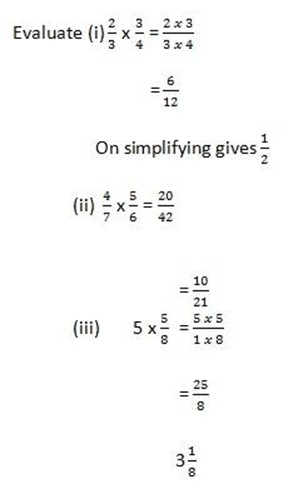
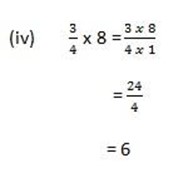
Dividing Fractions
1. When dividing fractions invert the second fraction then multiply the first fraction by the inverted fraction.

2. Before dividing number convert mixed numbers into improper fraction.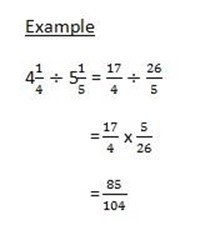

DECIMALS AND PERCENTAGES
Are fractions of tenth, they are written using a point which is a result of division of a normal fraction
E.g. 0.34, 0.5, 0.333——–
In the fraction 0.2546 the place values are
|
Ones |
Tenth |
Hundredths |
Thousandths |
Ten Thousandths |
|
0 |
2 |
5 |
4 |
6 |
edu.uptymez.com
Decimals can be converted into fractions and vice versa
E.g. Change 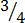 in to decimals
in to decimals
Solution:
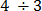 = 0.75
= 0.75
This fraction which ends after dividing is called terminating fraction. Other fractions do not end, these ones are called recurring or repeating decimals.
E.g. 

Conversion of Repeating decimal into fractions
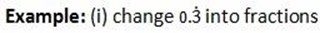
Solution:
0.3 = 0.333…….

Subtract (i) from (ii)
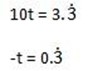
9t = 3.0
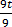 =
= 
t = 
Exercise 1
Insert 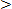 or
or 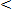 between each pair of fractions questions 4 to 12
between each pair of fractions questions 4 to 12
1.  ,
, 
Solution
L.C.M = 3

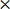 3 = 2
3 = 2

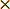 3 = 1
3 = 1

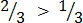
2.  ,
, 
Solution
L.C.M = 63

 63 = 7
63 = 7

 63 = 9
63 = 9


3. 

Solution

 12 = 10
12 = 10

 12 = 9
12 = 9


4.  ,
, 
Solution

 20 = 16
20 = 16

 20 = 15
20 = 15


5. 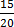 ,
, 
Solution
L.C.M of 20 and 4 = 80
 80 = 60
80 = 60

 80 = 140
80 = 140

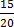
6.  ,
, 
Solution
L. C. M of 4 and 4 = 4

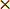 4 = 1
4 = 1

 4 = 3
4 = 3


7.  ,
, 
Solution
L. C. M of 5 and 6 = 30

 30 = 12
30 = 12

 30 = 5
30 = 5


8.  ,
, 
Solution
L. C. M of 9 and 6 = 18

 18 = 16
18 = 16

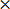 18 = 15
18 = 15

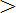

9. Which numbers are denominators in each of the following fractions?
(a) 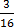 16 is the denominator.
16 is the denominator.
(b) 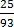 93 is the denominator
93 is the denominator
(c) 3 5 is the denominator
5 is the denominator
10. Which numbers are numerators in each of the following fractions?
(a)  Numerators is 3
Numerators is 3
(b) 3 Numerators is 4
Numerators is 4
(c) 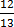 Numerators is 12
Numerators is 12
12. Which is greater
(a)  or
or 
Solution
Find the L.C.M of 5 and 4 = 20

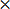 20 = 12
20 = 12

 20 = 15
20 = 15


(b)  or
or 
Solution
Find the L.C.M of 3 and 2 = 6
 x 6 = 4
x 6 = 4
 x 6 = 3
x 6 = 3

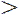

13. What is the condition for a fraction to be called improper?
The numerator is bigger than the denominator.
14. Change the following improper fractions into mixed numbers
(a)  = 1
= 1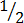
(b) 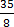 = 4
= 4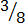
(c) 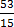 = 3
= 3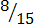
(d) 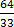 = 1
= 1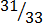
16 15. Change the following mixed numbers into improper fractions
(a) 3 
Solution
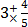
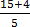
 =
= 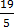
(b) 15 
Solution
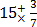
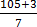
 =
= 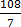
(c) 24 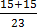
Solution
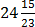
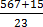
 =
= 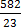
3.3 PERCENTAGES
Percentages are fractions expressed out of 100. That is – are the ones whose denominator is one hundred, they are denoted by (%) called percent
Example: 12% means 12 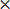
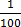 =
= 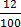
70% = 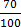 etc.
etc.
Examples: 1. convert the following percentage into fraction
(i) 65%
(ii)75%
(iii) 12  %
%
Solution
(i) 65%
65 
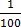 =
= 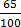 =
= 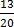
 =
= 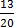
(ii) 75%
75 
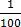 =
= 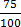 =
= 
 =
= 
(iii) 12  %
%
12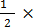
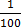 =
= 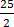
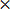
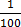 =
= 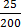
 12
12  % =
% = 
2. Change
(i) 40% into decimal
(ii) 35% into fractions
(iii) 0.125 into percentage
Solution
(i) 40% = 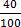 =
= 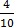
 = 0.4
= 0.4
(ii) 35%
35 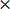
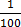 =
= 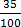
 =
= 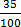
(iii) 0.125
Solution
0.125 = 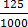
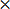 100%
100%
 = 12.5%
= 12.5%
3. Change the recurring decimals into fractions
(i) 0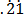
Solution
Let x = 0.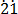 ……………………….. (i)
……………………….. (i)
100x = 21.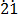 ……………………. (ii)
……………………. (ii)
Take away equation (i) from (ii)
100x = 21.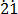
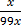 =
= 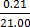
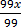 =
= 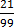
 x =
x = 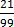
(ii) 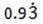
Solution
Let x = 0.9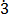 ……………………….. (i)
……………………….. (i)
10x = 9.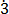 …………………………. (ii)
…………………………. (ii)
100x = 93.3 ………………………(iii)
Take equation (ii) away from equation (iii)
100x = 93.3
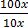 =
= 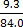
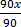 =
= 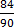
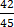
 x =
x = 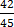
(iii) 0.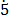 6
6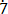
Solution
Let x = 0.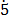 6
6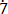 ………………………….. (i)
………………………….. (i)
1000x = 567.567 ……………………. (ii)
Take away equation (i) from (ii)
1000x = 567.567
X = 0.567
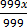
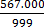
 x =
x = 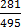
(iv) 0.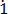 35
35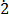
Solution
Let x = 0.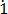 35
35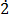 ……………………….. (i)
……………………….. (i)
10000x = 1352.1352 ……………………. (ii)
Take (ii) – (i)
10000x = 1352.1352
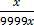 =
= 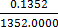
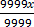 =
= 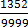
 x =
x = 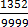
(v) 0.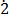 1
1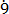
Solution
Let x = 0.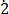 1
1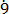 ………………………….. (i)
………………………….. (i)
1000x = 219.219 ……………………. (ii)
Take away equation (i) from (ii)
1000x = 219.219
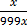 =
= 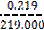
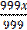 =
= 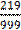
 x =
x = 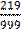
(vi) 0.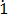 8
8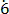
Solution
Let x = 0.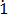 8
8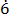 ………………………….. (i)
………………………….. (i)
1000x = 186.186 ……………………. (ii)
Take away equation (i) from (ii)
1000x = 186.186
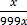 =
= 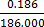
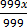 =
= 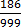
 x =
x = 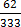
(vii) 0.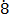 63
63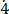
Solution
Let n = 0.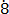 63
63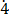 ………………………….. (i)
………………………….. (i)
10000n = 8634.8634 ……………………. (ii)
Take away equation (i) from (ii)
10000n = 8634.8634
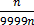 =
= 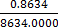
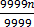 =
= 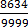
 n =
n = 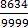
(viii) 0.7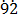
Solution
Let x = 0.7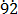 ……………………….. (i)
……………………….. (i)
10x = 0.7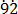 …………………………. (ii)
…………………………. (ii)
1000x = 792.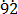 ………………………(iii)
………………………(iii)
Take away equation (ii) from equation (iii)
100x = 792.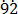
1000x – 10x = 792.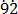 – 7.
– 7.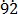
990x = 785
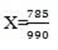
 x =
x = 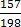
(ix) 0.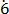 4
4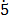
Solution
Let y = 0.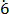 4
4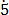 ………………………….. (i)
………………………….. (i)
1000y = 645.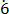 4
4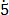 ……………….. (ii)
……………….. (ii)
Take away equation (i) from (ii)
1000y – y = 645-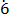 4
4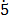
999y=645
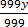 =
= 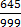
 y =
y = 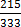
(x) 0.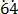
Solution
Let b = 0.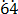 ………………………….. (i)
………………………….. (i)
100b = 64.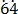 ……………………. (ii)
……………………. (ii)
Take away equation (i) from (ii)
100b – b = 64.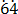 -0.
-0.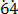
99b = 64
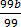 =
= 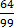
 b =
b = 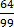
(xi)0.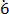 2
2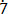
Solution
Let m = 0.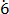 2
2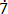 ………………………….. (i)
………………………….. (i)
1000m = 627.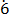 2
2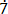 ……………………. (ii)
……………………. (ii)
Take away equation (i) from (ii)
1000m – m = 627.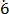 2
2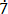 – 0.
– 0.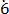 2
2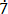
999m = 627
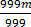 =
= 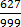
 m =
m = 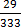
4. In question (i) to (v) change the fractions into decimals.
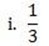
Solution
1 ÷ 3 =
 = 0.33
= 0.33
ii. 
Solution
5 ÷ 6 =
 = 0.833
= 0.833
iii. 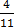
Solution
4 ÷ 11 =
 = 0.3636
= 0.3636
iv. 
Solution
1 ÷ 9 =
 = 0.111
= 0.111
v. 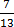
Solution
7 ÷ 13 =
 = 0.538461
= 0.538461

Solution
Let b = 0.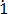 2
2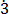 ………………………….. (i)
………………………….. (i)
1000b = 123.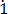 2
2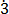 ……………….. (ii)
……………….. (ii)
Take equation (i) away from equation (ii)
1000b – b = 123.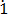 2
2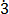 – 0.
– 0.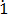 2
2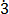
999b = 123
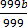 –
– 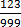
b = 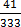
Operations on Decimals
Operations with decimals are similar to operations with whole numbers:
Addition
Note: The decimal points must be in line, put zeros at the end to give the same number of decimal places in each number.


Multiplication
Note:
- When multiplying decimals the answer must have the same number of decimal places as the total number of decimal places in the number being multiplied.
- First carry out the multiplication in the usual way, without any decimal points, then put the point to the total decimal places.
edu.uptymez.com

Division
Note:
It is not easy to divide by a decimal, so you multiply each number by a power of 10 in order that you are dividing by a whole number.
Example:- (i) Find (a) 68.32 ÷ 1.4
(b) 9.66 ÷ 0.23
Solution
(a) 68.32 ÷ 1.4 = 68.32 x 10 ÷ 1.4 x 10
682.2÷14
By long division
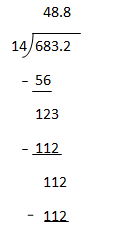
Therefore 68.32 ÷ 1.4 = 48.8
(b)
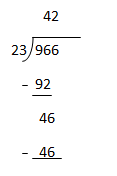
Therefore 9.66 ÷ 0.23 = 42

(c) 7.32 1.2 = 7.32 x 10 1.2 x 10
73.2
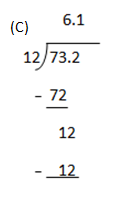
t
Therefore 7.32 ÷ 1.2 = 6.1
Mariam was given 20,000 shillings by her father, she spent 48% of it to buy shoes. How much money remained.
Solution
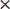 20,000
20,000
=9,600
20,000
– 9,600
11,600
∴ The remained money was 11,600/=
The remained money was 11,600/=


PERCENTAGES APPLIED TO REAL LIFE PROBLEMS
The examples below show the wide range of application
Examples:-
1. In one week, Flora earned 48,000/=, she spent 4,000/= on travel to and from work. What percentage of her money was left?
Solution: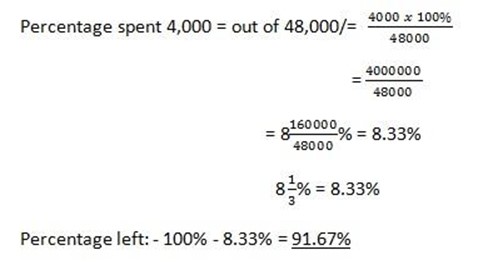
Percentage of a quantity
When finding a percentage of a quantity, it is often helps to change the percentage to a decimal and multiply it by the quantity.
Example:- Find (a) 20% of 840,000


Percentage increase and Decrease
There are two steps to calculate percentage increase (or decrease)
Example: In 1975 the population of a village was 90. It increased by 30% the following year. What was the population in the year 1976?
