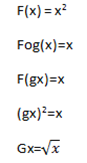ADVANCED MATHEMATICS FORM 5 – FUNCTION AND RELATION

COMPOSITE FUNCTION.

Two functions f and g are said to be composite function of fog= f(g) (x)

NOTE: COMMUTATIVE PROPERTY

Given f(x) = x²+1 and g(x)

=2x.

Find (i) fog(x)

       (ii).gof(x)

Approach f(2x) =2(x²+1)
1.fog(x) = f (g(x)

f(2x) = (2x)² +1

        =4x²+1
2. gof(x) = g f(x)   =

=g(x²+1)=

=2(x²+1)

CONCLUSION

fog gof, hence the compacite function is not commutative

ASSOCIATIVE PROPERTY

Given

F(x)=x²-1, g(x)=3x and h(x) =2/x

 (i)(fog)  oh

(ii)fo (goh)

fog=f (gx)=f(3x)=(3x)²-1

9x²-1

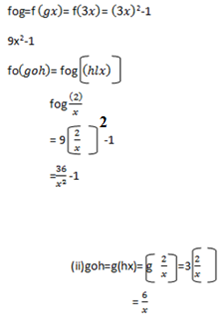
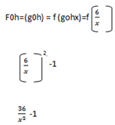
Since fo(goh)=fo(goh) hence the compacite function is associative property

FUNCTION

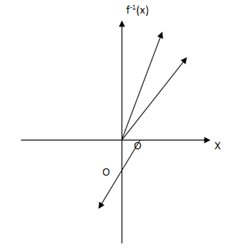
A f unction is a function when the line parallel to the y-axis cuts only once on the curve.

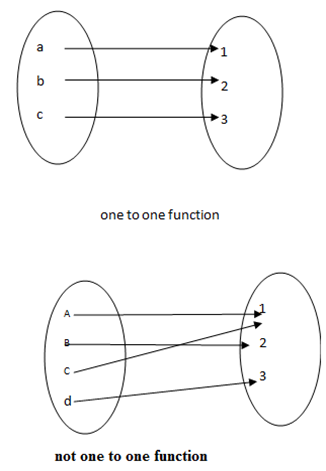
The line parallel to the x-axis cuts the curve only

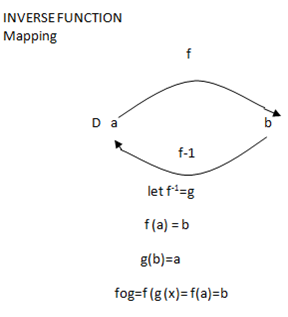
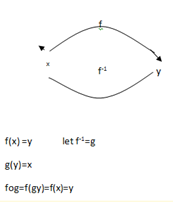
 -An inverse function is the one which each elements from Domain matches exactly in range conversely each element from range matches exactly with Domain

Given f(x)=2x-1

Find f^-1(x)

Approach

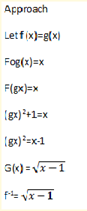
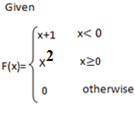
Sketch

(i) f(x) – state its Domain

(ii)f^-1 (x)

soln

f(x)=x+1

suppose f^-1(x) = g(x)

fog=f(gx)=x

gx+1=x

gx=x-1