GRAPHS OF FUNCTIONS
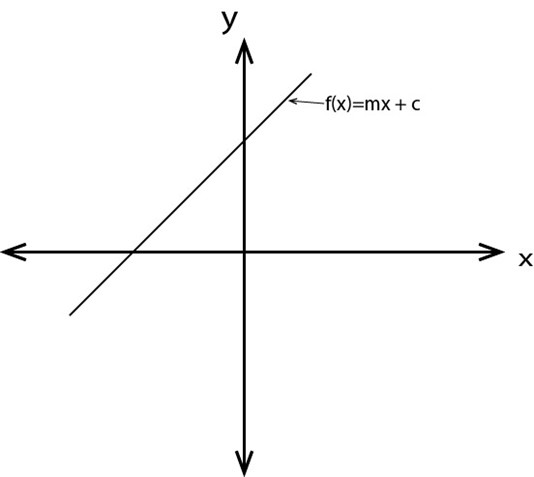
A) Linear function
If the function of the form f (x) = mx +c
M = slope
C = constant
Examples
1.) Draw graphs of the following and give their domain and range
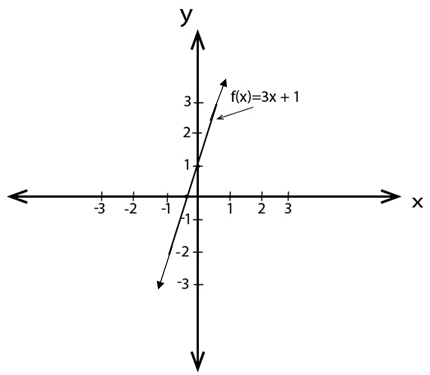
f (x) = 3x +1
Solution
f (x) = 3x+1
Intercept
When x = 0, y = 1
y = 0, x = 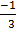
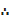 Domain =
Domain = 
Range = 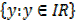
2) f(x) = 6
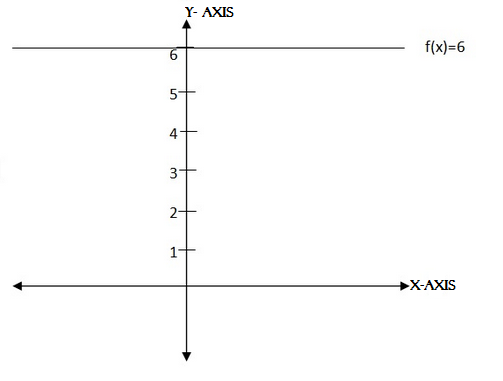
Domain = 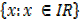
Range = 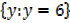
Note
f(x) = a is called the constant function
Exercise
1) Given that f(x)=x2 and g(x)=x
Find the domain and range of
a) f (x) + g(x)
b) f (x) – g (x)
c.) f (x) g (x)
d) f (x) – g(x)
2) Draw graphs of
a.) f(x)= -3x+1
b.) f(x) = 3x-1

d.) f( x ) = ½ – x
Solution
1a) f(x) +g(x)
y = x2 + x
TURNING POINTS OF A QUADRATIC FUNCTION
Step function
Are functions which are not continuous.
Example
Draw the graphs of the following function give its
Domain and range
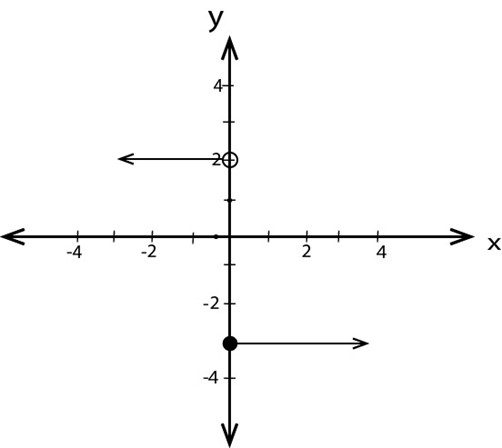
f(x) = 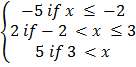
Solutions
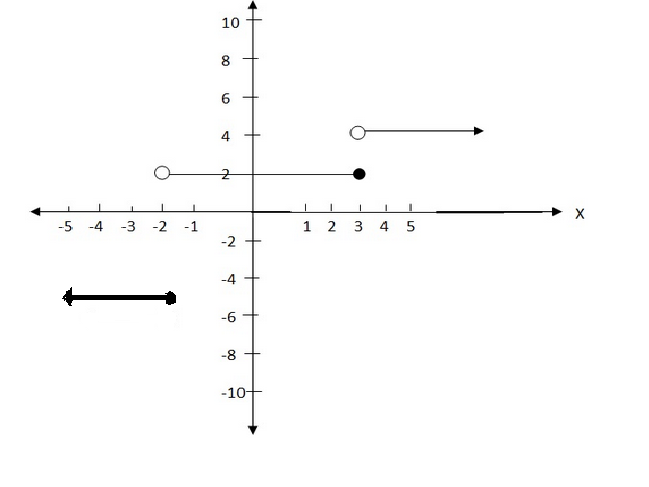
Domain = 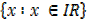
Range = 
C) QUADRATIC FUNCTIONS
Is the function of the form
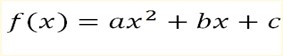
Where a 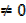
Example
Draw the graph of
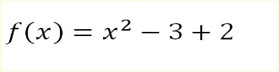
Solution
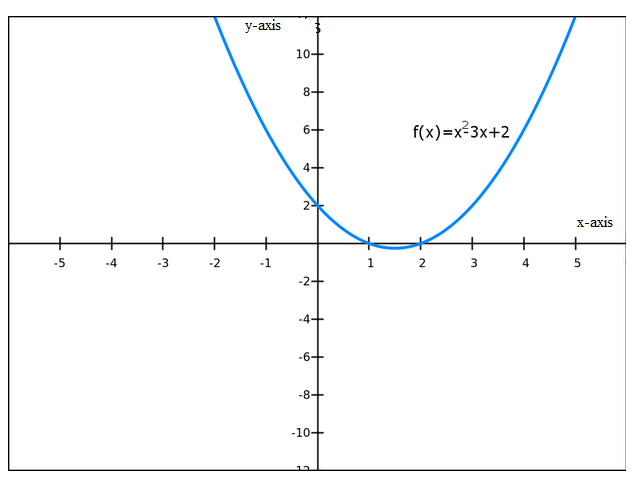
Exercise
1. Draw the graphs of the following functions give the domain ad the range
i) f (x)= 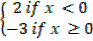
ii) f(x)= 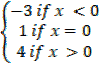
ii) f(x) = 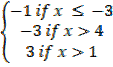
2. Draw graphs of the following functions
a) i) 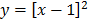
b) ii) 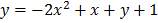
c) iii) f(x)= x2-x
d) iv) g(x)= -4x2-1
Solutions
f (x ) = 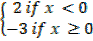
Domain = 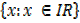
Range = 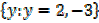
TURNING POINTS OF QUADRATIC FUNCTION
Given the function
f(x)=ax2+bx+c where a, b and c are constants
By completing the square
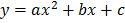
y = 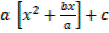
= 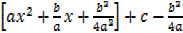
= 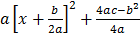
y = 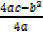
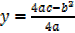
(Case :1)
If a 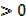 then a( x +
then a( x + 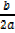 )2≥0
)2≥0
Therefore
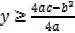
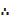 The function is minimum
The function is minimum
When y = 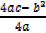 and
and 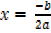
(Case 2)
If a  then a [x +
then a [x +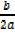 ] 2
] 2
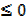
 y =
y = 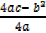
 The function maximum when
The function maximum when 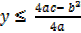 and
and 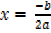
Note
The maximum and the minimum points are the turning points of quadratic function
Examples (1)
Find the turning points of the function
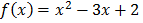 → y = x2 – 3x + 2
→ y = x2 – 3x + 2
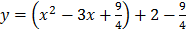
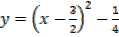
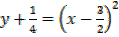
Therefore x = 3/2 , y = – ¼
Therefore turning point = (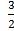 , -1/4)
, -1/4)
Alternatively:
x = -b/2a , y = 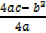
a = 1, b = -3, c = 2
Therefore x = 3/2
y = -1/4
Example 2
Find the turning point of the function
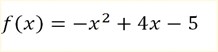
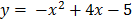
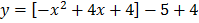
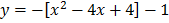
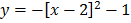
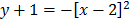
x = 2, y = -1
Turning point = (2, -1)
Example 3
Find the domain and range of the function
p(x)=-x2+4x-5
Solution
Domain = 
Range = 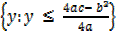
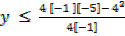
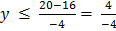
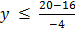 =
= 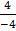
Range
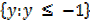
Exercise
1) Find the turning points of the following
a.) f (x) = x2 -4x + 2
b.) f (x) = x2 + 8x + 5
c.) f (x) = 5 -6x – 9 x2
d.) f (x) = 3x2 + 8x – 1
e.) f (x) = x2 -4x – 5
2) Find the domain and range
a.) f (x) = x2 – 4x + 2
b.) f (x)= 3x2 +8x – 1
c.) f (x) = -5 – 6 – 9x2
d.) f (x) = 2 –x – x2
e.) f (x) = x2 – 4x +2
Solution
a) 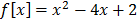

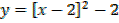
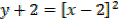
Turning point= ∴ x = 2, y = -2
Turning point=(2,2)
b) 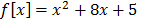
Solution

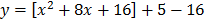

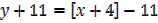
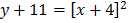
x = – 4
And
y = – 11
Therefore Turning point = (-4, -11)
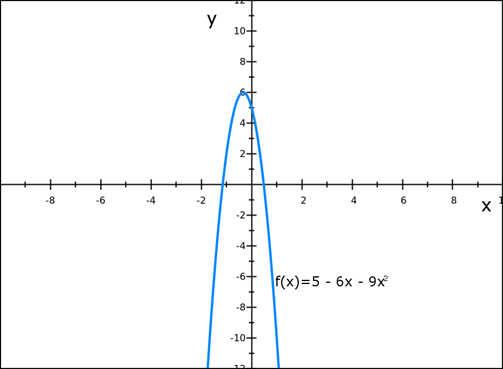
c) f ( x) = 5- 6x- 9x2
Since
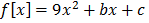

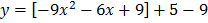
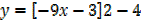
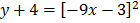
y = -4 , x = 1/3
Turning point = ( 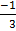 , – 4)
, – 4)
d) f (x) = 3x2 +8x – 1
Solution
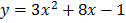
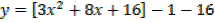
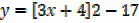
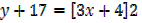
x = -4/3 , y = -17
Turning point =(-4/3, -17)
Alternatively
x = -b / 2a
x = -8/2 [ 3]
x = -8/6
x = -4/3
x = -4/3
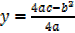
= 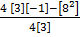

y = -19/3
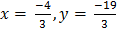
Turning point = 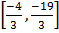
e) f (x) = x2 – 4x -5
Solution
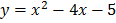
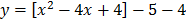
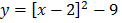
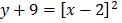
x= 2, y = -9
Turning point =(2,-9)
Alternatively
x = -b/2a
x = -[ -4 ][ 1]
x = 4/2
x = 2

= 
= 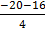
= 
= -9
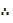 Turning point = (2,-9)
Turning point = (2,-9)
2 a) 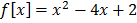
Domain = 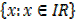
Range = 
y ≥ -8/4
y ≥ -2
Range = 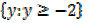
∴ Domain = 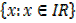
Range = 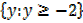
b) f (x) = 3x2 + 8x – 1
Solution:
Domain = 
Range = 
y ≥ 19/3
Range ={ 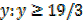 }
}
Domain = 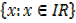
Range = 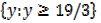
C) f (x) = 5 – 6x – 9x2
Solution
y = -9x2 – 6x + 5
Domain = { x : x ┇IR}
Range = { y : y ≤ 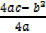 }
}
y 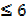
 Domain =
Domain = 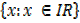
Range = 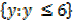
Using intercepts and turning points to sketch the graph of quadratic functions
Example
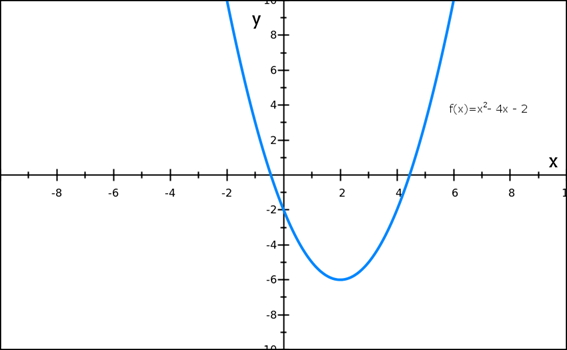
Sketch the graph of
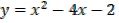
Solution
y – Intercept
When
x = 0, y = -2
x- Intercept
When
y= 0, x2– 4x – 2 = o
x = 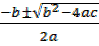
x = 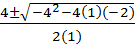
x = 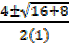
x = 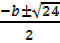
x = 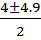
x =  or
or 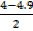
x= 4.5 OR x = -0.5
Turning point
x = 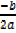
x = 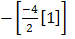
x = 2


= 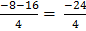
= – 6
Turning points = (2,-6.)
Since a  the function has a minimum value therefore the graph opens upwards
the function has a minimum value therefore the graph opens upwards
Exercise
Sketch the graphs of the following functions using intercepts and turning points
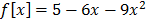
Solution
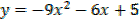
y intercept
When x = 0, y = -5
x intercept
When y = 0, -9x2 -6x +5 = 0
x = 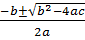
x = 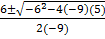
x = 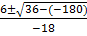
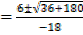
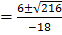
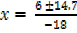
Either x
= 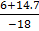 or
or 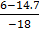
x = 20.7/-8 or -8.7/-18
x = -1.2 or x = 0.5
Turning points
x= -b/2a
x = – [-6/2 [-9]
x =- 1/3 or – 0.3
y = 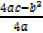
y = 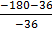
y = 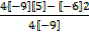
y = 
y= 6
Turning points = (-0.3 , 6)
Since a 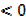 the function has a maximum value therefore the graph opens down wards
the function has a maximum value therefore the graph opens down wards
2) f(x) = 3x2 + 8x -1
Solution
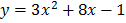
y – Intercept
When x=0, y = -1
x – Intercept
When y = 0, 3x2 +8x-1=0
x = 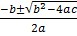
x = 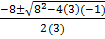
x = 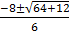
x = 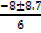
Either
x = 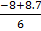 or
or 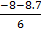
x = 0.12 or -2.8
Turning points
x= -b/ 2a
x = -8/ 2 [3]
x = -8/6
x = -4/3 or -1.3
y = 
y = 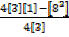
y = 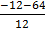
y = 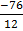
y = -6
Turning points = (-1.3,-6)
Since a 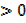 the function has a minimum value therefore the graph opens upwards
the function has a minimum value therefore the graph opens upwards

D) Cubic function
Is a function of a form f (x) = ax3 + bx2 – (x + d) where a, b, c and d are real numbers
a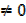
Example
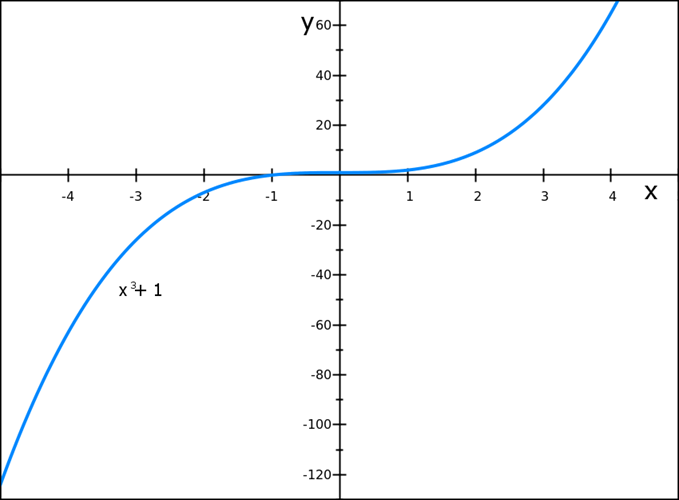
Draw the graphs of f (x) = x3 +1
Solution