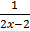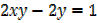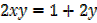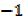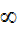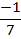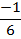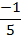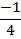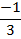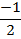E)Rational function
Is the function which can be defined by rational fraction such that both the numerator and denominator are polynomials.
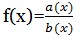
Where b(x)≠0
b 
Or is the function of the form f(x)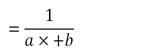
where a and b are real numbers.
Example
Sketch the graph of
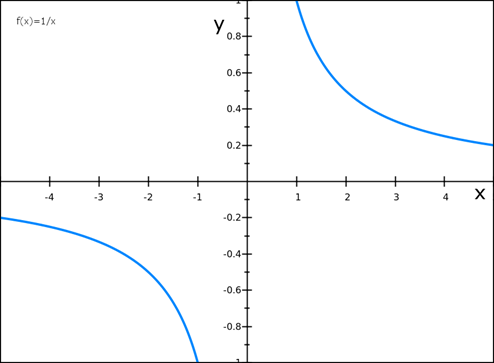
1) f (x) = 1/x
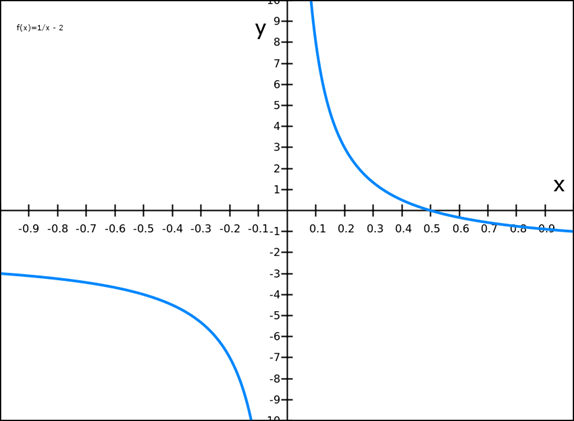
2). f (x) = 1/ x-2
Solution
1) f ( x ) = 1/x
Solution
2) f( x) = 1/x -2
NOTE:
The point where the function is not defined is called the a asymptote
Exercise
Draw the graphs of the following functions
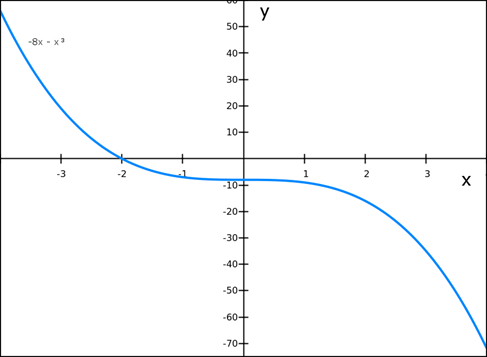
i.) f( x)= -8 – x3
ii.) f(x) = 9 – x –x2– x3
iii.) f(x) = x3 – 3x2 +3
iv.) f(x) = 8 – 3x3
v.) f(x) = 2/x-1
vi.) f(x) = 6/ x-6
vii.) f(x) =1 / x+3
viii.) f(x) = 5/ x+1
Solution
F (x) = -8 – x3
Sketching graphs by using intercepts and asymptotes
Example
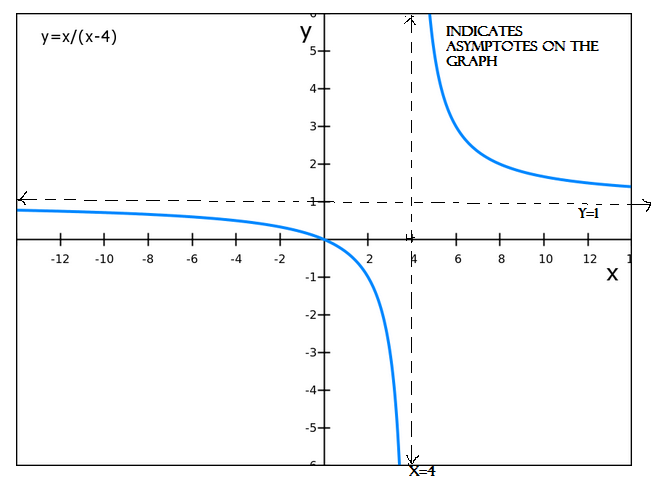
Sketch the graph of
y = 
Steps
1) Find the vertical and horizontal asymptotes
2) Draw the asymptotes on the xy plane by using dotted lines except when they coincide with the axes
3) Test the neighborhood points of the asymptotes to get the direction of the graph
4) Find the intercept [x – intercept and y – intercepts]
5) Join the arrows / points by using a free hand
Solution
∴ Vertical asymptote
Set x – 4 = 0
x = 4
Vertical asymptote is the line where x = 4
Horizontal asymptote
Make x subject
y =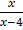 
y[x – 4] = x
yx – 4y = x
yx – x = 4y
x [y – 1] = 4y
x = 4y / y – 1
Set
y – 1= 0
y = 1
Horizontal asymptote is the line where y = 1
y = intercept = 0
x – Intercept = 0
Exercise
Sketch the graphs of the following functions by using intercept and asymptotes
1) y =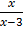 
2) y =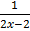 
3) y =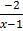 
4) y =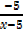 
5) y = 
Solution
y =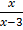 
Vertical asymptote
Set x – 3= 0
X = 3
Vertical asymptote of the line where x = 3
Horizontal asymptote
Set x subject
y =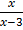 
y [x -3]= x
yx – 3y = x
yx – x = 3y
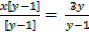
y =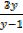 
Set y -1 = 0
y = 1
Horizontal asymptote is the line where y = 1
y – Intercept = 0
x – Intercept = 0
x = 1
2x – 2
Solution
Vertical asymptote
Set 2x-2 = 0
=
x = 1
Horizontal asymptote
Make x the subject
y = 
