ADVANCED MATHEMATICS FORM 6 – HYPERBOLIC FUNCTION

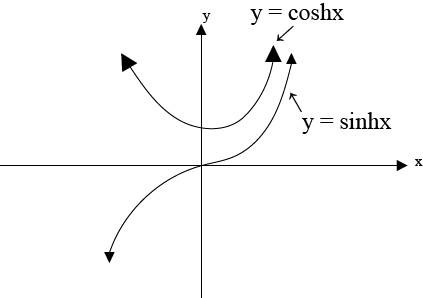
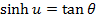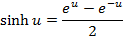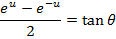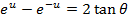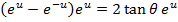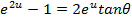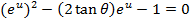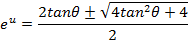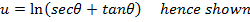COMBINATION OF COSHX AND SINHX

Examples

         1. Show that

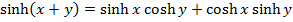
         2. Show that

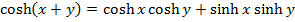
        3.  Show that

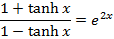
         4. Show that

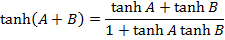
    5.   Find the expression that equation 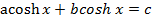  has equal roots

        

         6. Show that the point 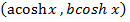lies between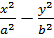

         7. Solve the following
(i)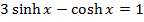

        
8.Solve the following equation  give the roots in terms of  natural logarithms

         if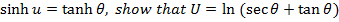

Solution 01

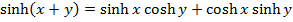
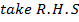
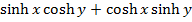
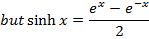
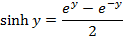
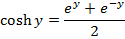
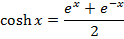
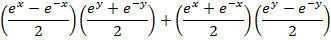
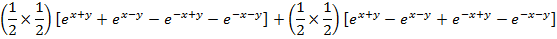
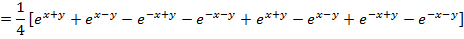
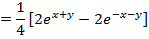
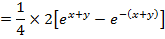
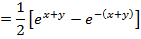
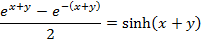
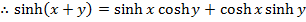
Solution 2  

         










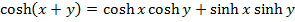
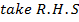
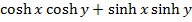
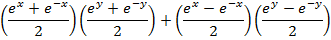
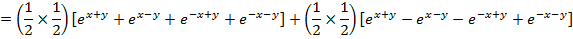
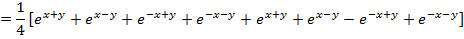
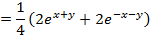
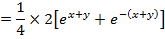
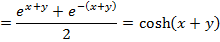
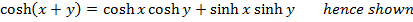
Solution 03

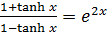
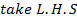
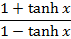
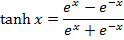
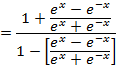
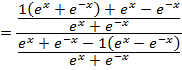
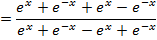
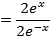
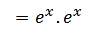
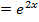
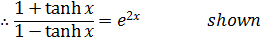
Solution 04

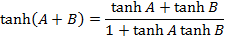
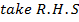
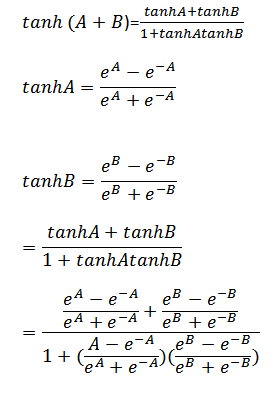
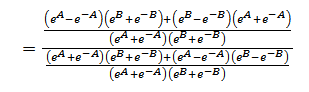
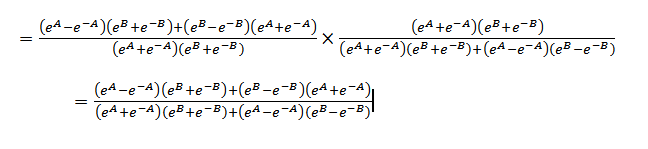
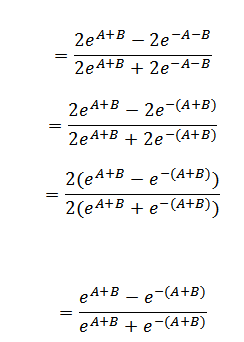
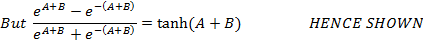
Solution 05

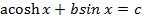
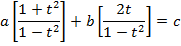
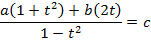
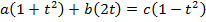
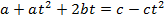
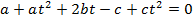
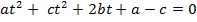
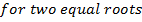
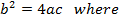
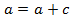
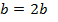
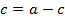
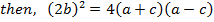
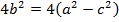
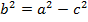
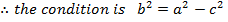
Solution 06

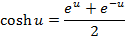
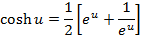
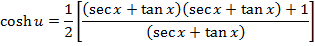
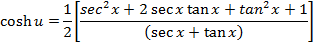
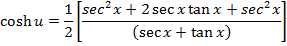
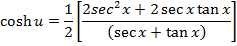
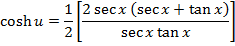
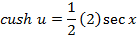
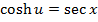
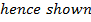
Solution 07

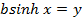
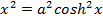
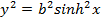
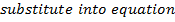
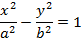
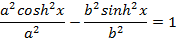
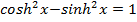
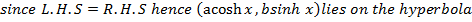
Solution 08

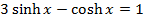
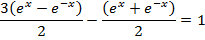
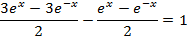
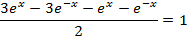
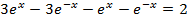
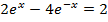
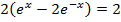
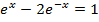
Divide by e^-x throughout.

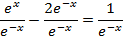
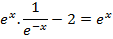
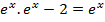
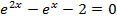
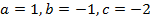
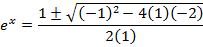
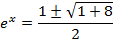
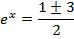
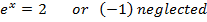
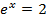
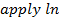
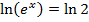
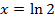
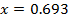
Solution 09

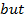
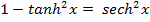
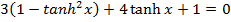
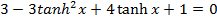
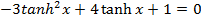
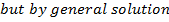
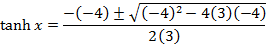
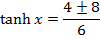
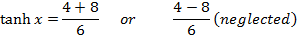
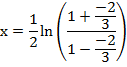
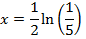
Solution 10