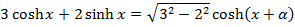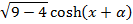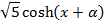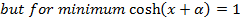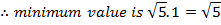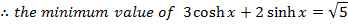OSBORN’S RULE
This is the rule used to change the trigonometrical identification into corresponding analogous hyperbolic identities.
Osborn’s rule states that “whenever a product of two series occurs change the sign of that term “
Examples
1. Change the identity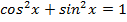 
into analogous hyperbolic identity
Solution
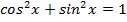
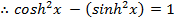
2. Write the analogous hyperbolic identity for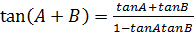 
Solution
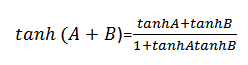
3. Change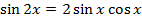 
into a corresponding hyperbolic identity
Solution
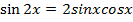
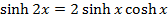
INVERSE OF HYPERBOLIC FUNCTION
The inverse of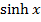 
or 
The inverse of 
is denoted by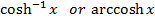 
The inverse of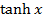 
is denoted by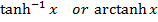 
GRAPHS OF INVERSE OF HYPERBOLIC FUNCTIONS
The graph of the inverse of hyperbolic functions is a reflection of graphs of hyperbolic function on the inverse of y = x
(a)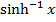 
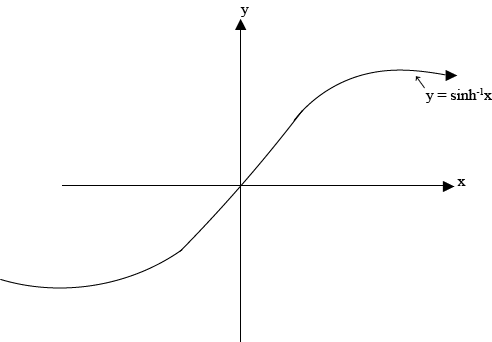
(b)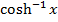 
Concept:
y = 
is not one to one function in such a way it can’t have inverse without restriction otherwise its inverse will not be a function but just a relation. For y =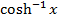
to be a function the domain of y =
should be restricted such that domain is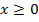 
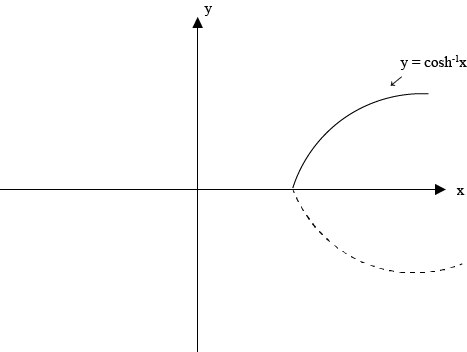
(c)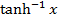 
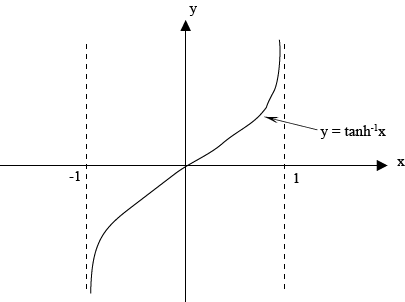
(d) For y =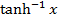
it is defined by only for -1 < x < 1
EXPRESSION OF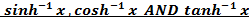
IN LOGARITHMIC FORM
( a) 
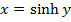
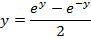
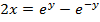
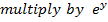
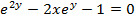
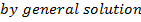
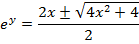
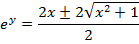
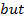
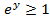
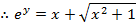
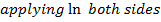
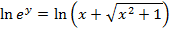
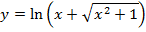
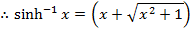
(b b) 
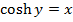
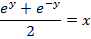
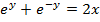
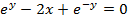
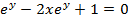
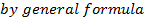
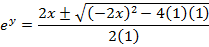
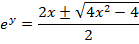
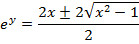
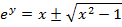
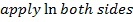
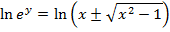
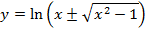
This is the expression for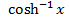
as just a relation and not a function.
For
being in function
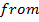
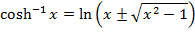
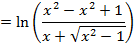
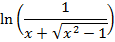
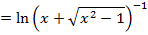
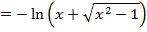
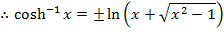
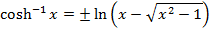
(c c)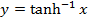 
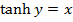
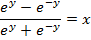
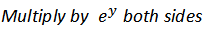
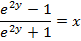
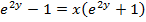
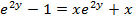
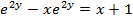
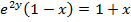
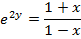
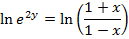
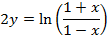
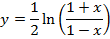
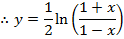
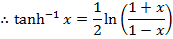
Examples
1. (i)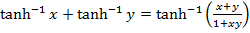 
(ii)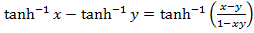
Solution (i)
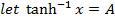
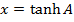
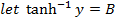
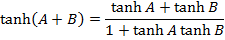
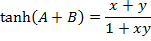
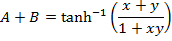
Solution (ii)
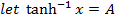
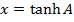
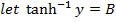
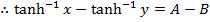
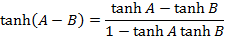
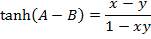
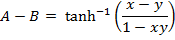
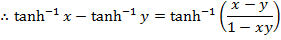
2. Prove that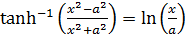 
Solution
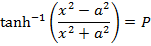
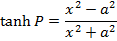
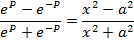
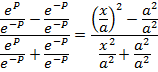
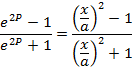
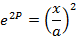
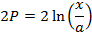
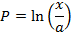
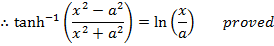
3. If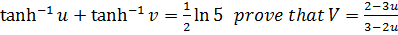 
Solution
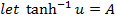
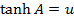
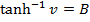
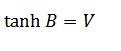
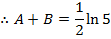
1
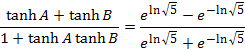
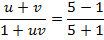
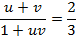
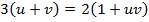
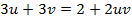
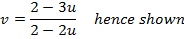
4.. Given that 
Solution
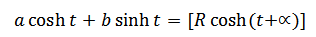
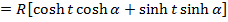
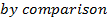
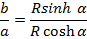
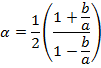
R- FORMULAE
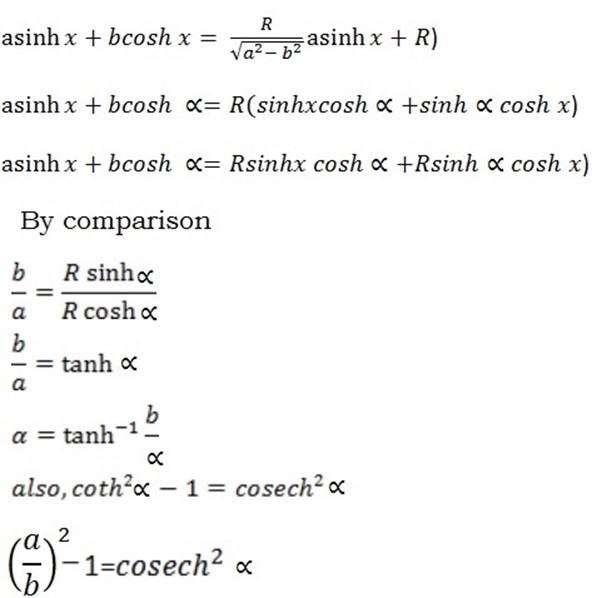
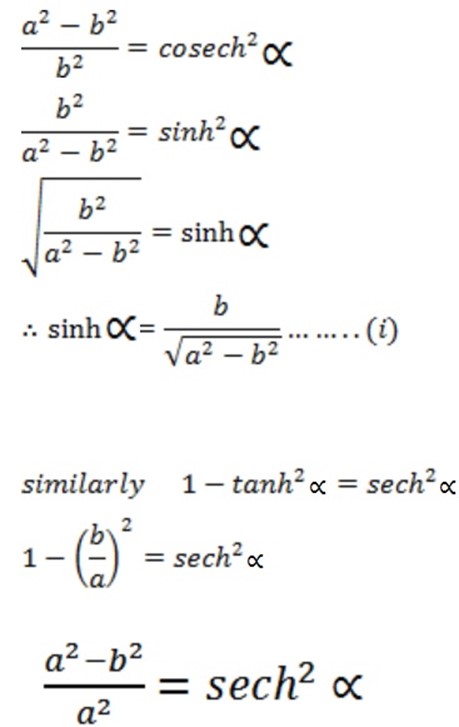
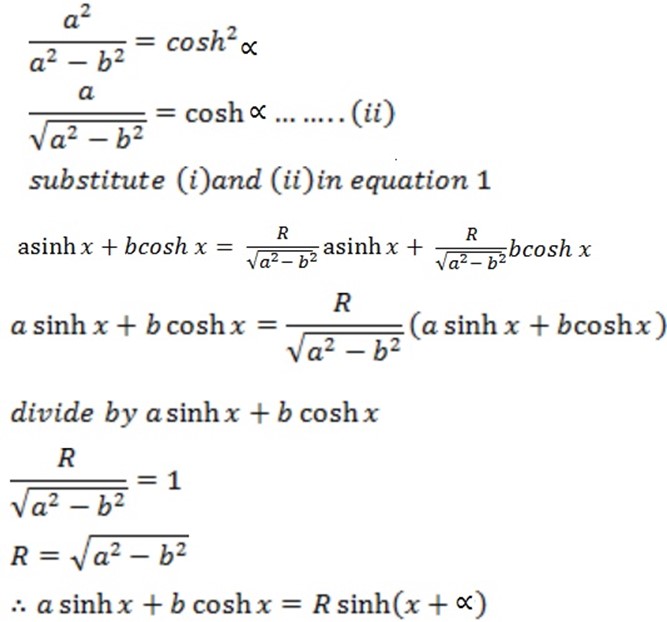
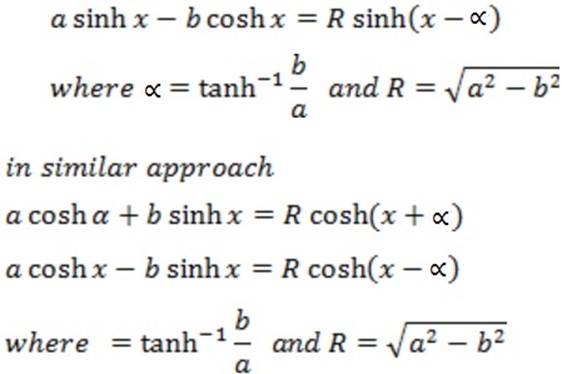
Examples
Find the maximum value of
3 coshx + 2sinh∝
Solution
