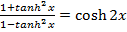CALCULUS OF HYPERBOLIC FUNCTION
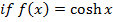
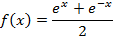
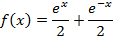
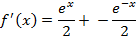
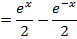
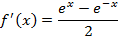
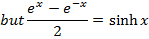
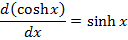
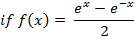
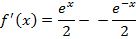
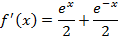
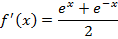
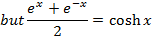
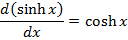
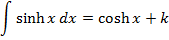
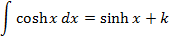
All other types of hyperbolic functions are differentiated or integrated by the concept of the above results
Note;
In calculus of the hyperbolic functions of the Osborn’s rule never operated.
Examples
→Differentiate with respect to x
a) 
b) 
Solution (a)
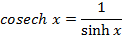
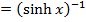
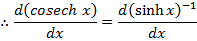
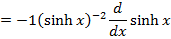
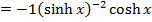
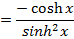
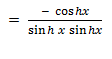
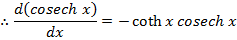
→Differentiate
a) 
b)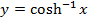 
Solution (b)
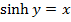
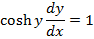
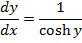
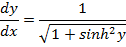
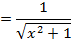
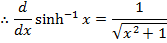
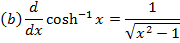
→Evaluate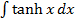 
solution
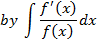
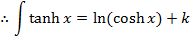
→ Evaluate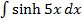 
Solution
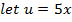
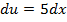
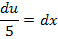
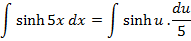
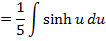
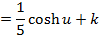
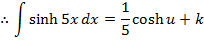
→Evaluate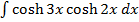 
Solution
→
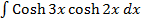
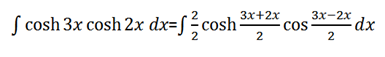
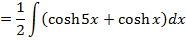
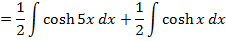
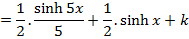
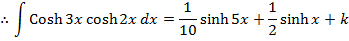
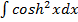
Solution
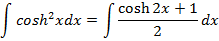
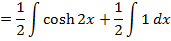
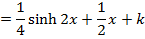
QUESTIONS
1) Express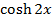 
and 
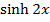into exponential form and hence solve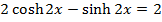 
2) Given that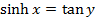 
. Show that 
3) Prove that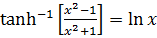 
4) Solve for real values of x. 
5) Prove that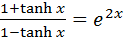 
6) (a) If 
, prove that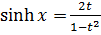 
(b) use the result in (a) to solve the equation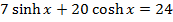 
7) If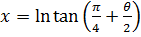 
fin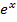d 
and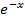 
and hence show that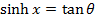 
8) Prove that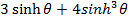 
9) If 
Prove the fact that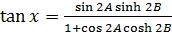 
10) Find the coordinates of the point of intersection of the graph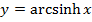 
and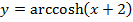 
11) If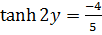 
show that 
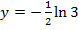and find the value of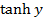 
12) Show that the curve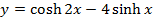 
has just one stationary point and find its coordinates and determine its nature.
13) Prove that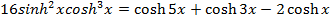 
14) Prove the fact that 
15) Express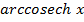 
in logarithmic form hence solve the equation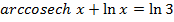 
16) Show that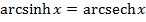 
has only one root and its root is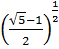 
17) Show that 