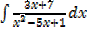Integration :Is the reverse process of differentiation, i.e. the process of finding the expression for y in terms of x when given the gradient function.
The symbol for integration is , denote the integrate of a function with respect to x
, denote the integrate of a function with respect to x
If 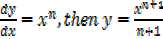
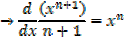
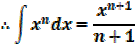
This is the general power of integration it works for all values of n except for n = -1
Example
1. 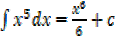
2. Integrate the following with respect to x
(i)3x2
Solution
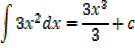
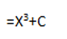
Integration of constant
The result for differentiating c x is c
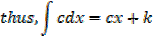
Properties
(1) 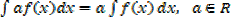
(2) 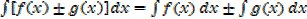
Integration by change of variables
If x is replaced by a linear function of x, say of the form ax + b, integration by change of variables will be applied
E.g. 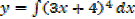
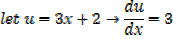
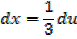
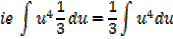
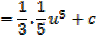
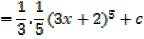
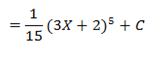
Considering 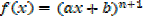 in similar way gives the general result
in similar way gives the general result
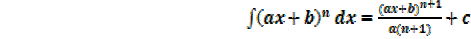
Example
Find the integral of the following
a) (3x – 8) 6 b) 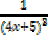
Solution (a)
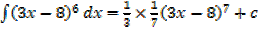
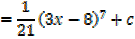
Solution (b)
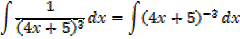
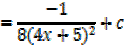
→ If 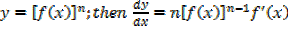
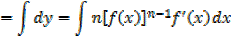
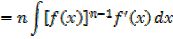
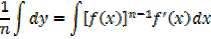
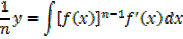
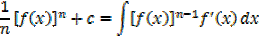
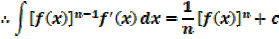
Example
1. Find 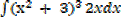
Solution
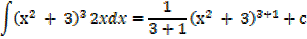

2. Find 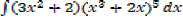
Solution
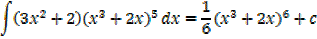
Integration of exponential function
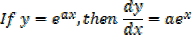
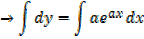
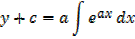
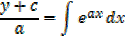
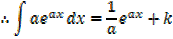

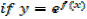

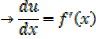
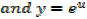
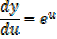
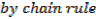
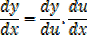
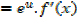

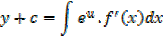
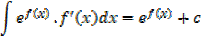
Example 01
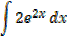
Solution
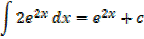
Alternative
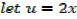
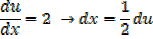
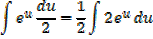
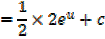
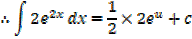
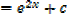
Example 02
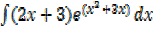
Solution
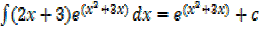
Alternative
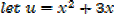
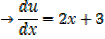
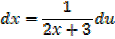
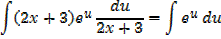
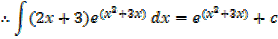
Integrating fraction
If 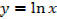
Differentiating with respect to x gives
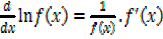
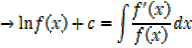
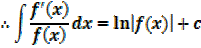
Example
1. 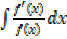 ,given that f(x)=x2+1
,given that f(x)=x2+1
Solution
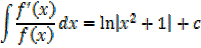
2. Find 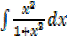
solution

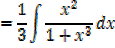

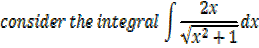
Note: 2x is the derivative of x2 + 1 in this case substitution is useful
i.e. let u = x2 + 1
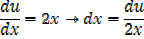
This converts into the form 
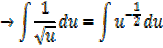
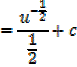
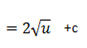
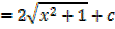

Standard integrals
· 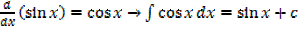
· 
· 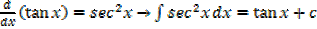
· 
·  →∫sec x tan xdx=sec x+c
→∫sec x tan xdx=sec x+c
· 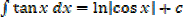
· 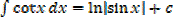
· 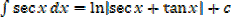
· 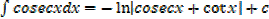
· 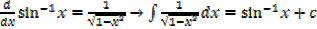
· 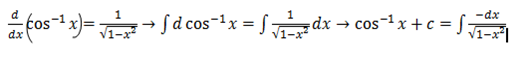
· 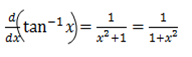
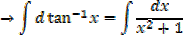
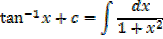
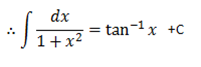
· 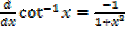
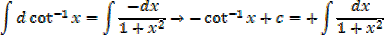
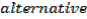
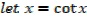
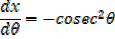
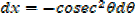
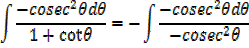
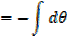
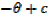
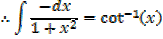
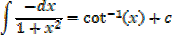
EXERCISE
Find the integral of the following functions
 i)
i) 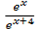
ii) 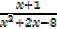
iii) 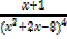
iv) 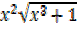
Integration by partial fraction
Integration by partial fraction is applied only for proper fraction
E.g. 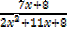
Note that:
The expression is not in standard integrals
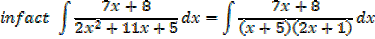
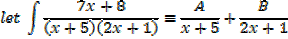
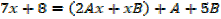
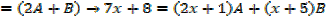


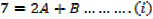
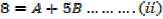
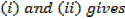
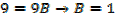



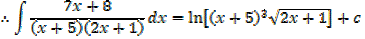
Example 01

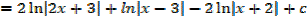
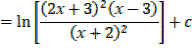
Example 02
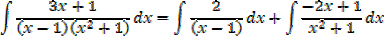
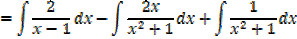
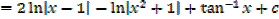
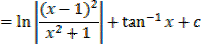
Improper fraction
If the degree of numerator is equal or greater than of denominator, adjustment must be made
Example
1. Find 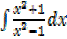
Solution
Both numerator and denominator have the degree of 2
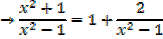
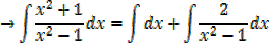

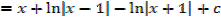
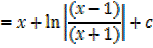
2. 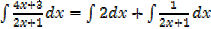
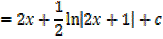
3. 
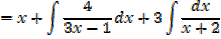
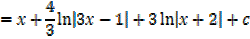
If the denominator doesn’t factorize, splitting the numerator will work
→ Numerator = A (derivative of denominator) + B
Example
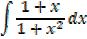
Solution
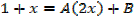
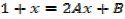
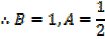
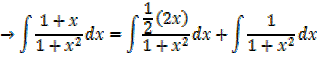

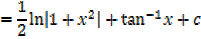
Important
It can be shown that
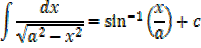
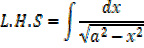
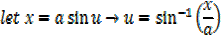

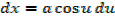
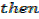
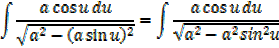
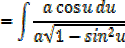
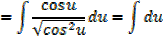
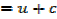
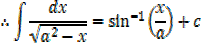
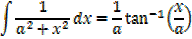

EXERCISE
I. 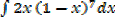
II. 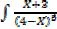
III. 
Integrated of the form

Note that:
1. If the denominator has two real roots use partial fraction
2. If the denominator has one repeated root use change of variable or recognition
3. If the denominator has no real roots, use completing the square
E.g.
I. 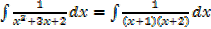
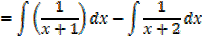

II. 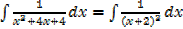
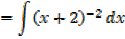
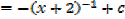
III. 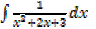
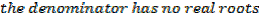
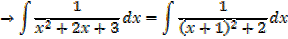
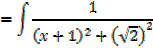
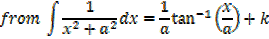
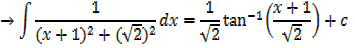
Integral of the form
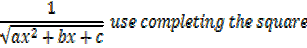
Example
→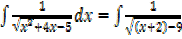
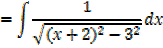
Then hyperbolic function identities is identities is used 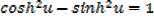
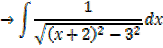
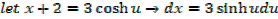
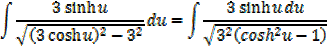
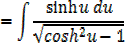
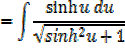
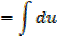
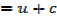
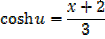
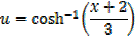
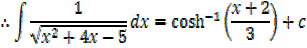
Note that:
If the quadratic has 1 represented root, it is easier
E.g.

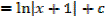
EXERCISE
Find the following
i. 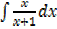
ii. 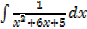
iii. 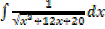
iv. 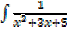
v.