ADVANCED MATHEMATICS FORM 5 – INTEGRATION

APPLICATION OF INTEGRATION

To determine the area under the curve

Given A is the area bounded by the curve y=f(x) the x -axis and the line x=0 and x=b where b> a

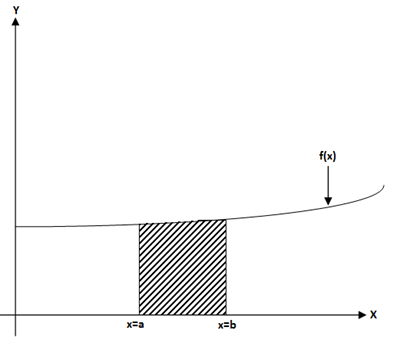
The area under that curve is given by the define definite integral of f(x) from a to b

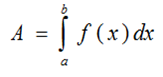
          = f (b) – f (a)

Examples

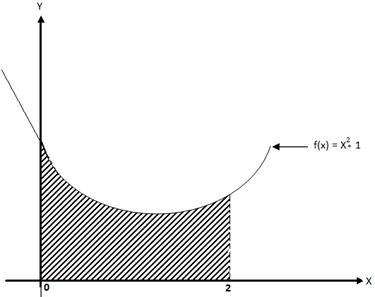
1. Find the area under the curve f(x) =x²+1 from x=0 to x=2

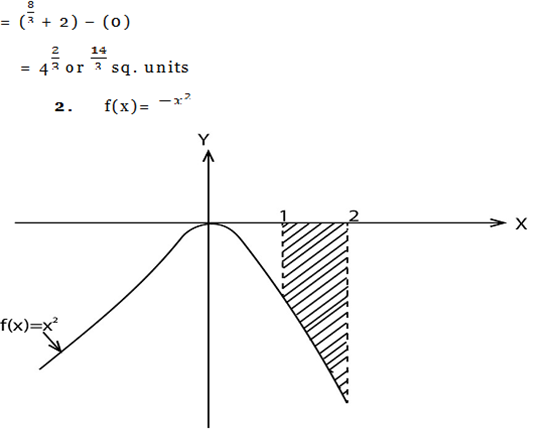
2. Find the area under the curve f(x) = from x=1 to x=2

3. Find the area bounded by the function f(x) =x ²-3, x=0, x=5 and the x- axis

Solution

1. f(x) =  + 1
   

edu.uptymez.com

      y intercept=1

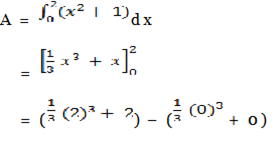
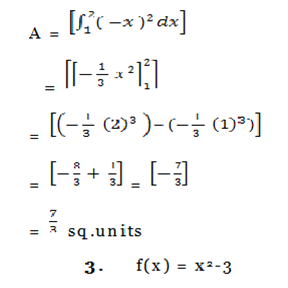
EXERCISE

1.      Find the area between y = 7-x² and the x- axis from x= -1 to x=2

2.      Find the area between the graph of y=x² x – 2 and the x- axis from x= -2 to x=3

Solution

^1.        y =7-x²

Where y- intercept =7

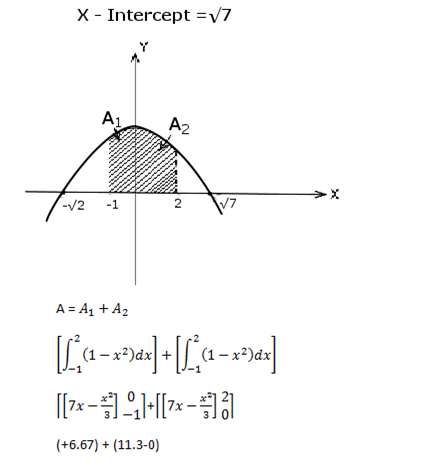
= 6.67 + 11.3

=17.97sq units

Volume of the Solids of Revolution

The volume,V of the solid of revolution is obtained by revolving the shaded portion under the curve, y= f(x) from x= a to x =b about the x -axis is given by

Example 1

Find the volume of revolution by the curve y=x² from x=0 to x=2 given that the rotation is done about the the x- axis

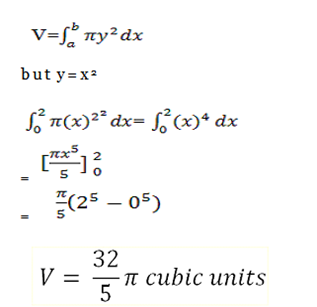
Exercise

1. Find the volume obtained when each of the regions is rotated about the x – axis.

a) Under  y= x³, from x =0 to x=1
b) Under y²= 4-x, from x=0 to x=2
c)Under y= x², from x=1 to x=2
d)Under y= √x, from x=1 to x=4

2. Find the volume obtained when each of the region is rotated about the y-axis.
a) Under y= x², and the y-axis from x=0 to x=2
b) Under y= x³, and the y-axis from y=1 to y=8
c) Under y= √x, and the y-axis from y=1 to y=2

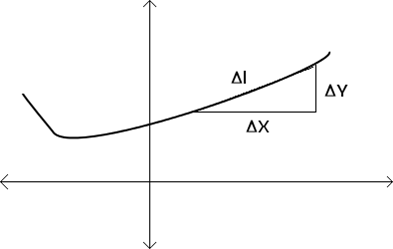
 LENGTH OF A CURVE

                   Consider the curve

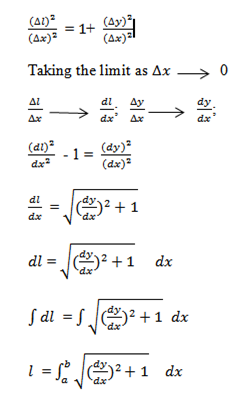
Example

Find the length of the part of the curves given between the limits: