DEFINITE INTEGRAL
The definite integral is given by
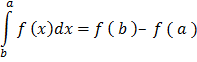
Where a = is the lower limit
b = is the upper limit
Note:
The arbitrary constant is not shown in the definite integral
Examples
1. 
Solution

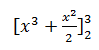
= 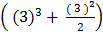 –
– 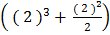
=  –
– 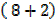
= 31  – 10
– 10
= 21 
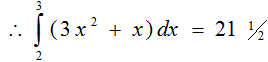
2. 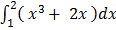
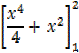
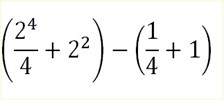
= 8 – 1
= 6
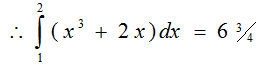
EXERCISE
Find the value of
1. 
2. 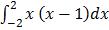
3. 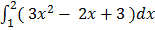
4. 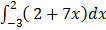
5. 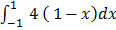
Solution
1. 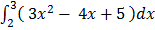
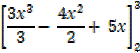
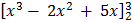
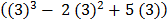 –
– 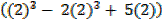
(27 – 18 +15) – (8 – 8 + 10)
(27 – 3) – (8 + 2)
= 14
2. 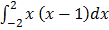
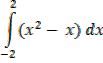
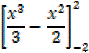
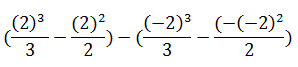
(  – 2) – (-
– 2) – (-  –
–  )
)
(  – 2) – (
– 2) – (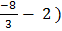
 + 4
+ 4
= 5
3. 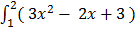
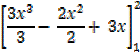
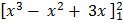
(  – (
– ( 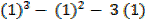
(8 – 4 + 6) – (1 – 1 + 3)
(8 + 2) – (1+2)
= 7
4. 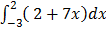
Solution
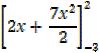
(2(2) +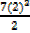 ) – (2(-3) + 7
) – (2(-3) + 7  )
)
(4 + 14) – (-6 +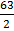 )
)
18 – (25 )
)
= -7
INTEGRATION BY SUBSTITUTION METHOD
Integrate the following with respect to x
1. (3x-8)6
2. 4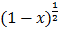
3. x 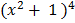
Solution
1. 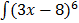 dx
dx
Let u = 3x – 8
du=3dx
 du =
du = 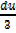
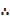
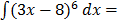
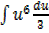
= 
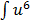 du
du
=  x
x
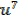 + c
+ c
= 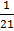
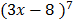 + c
+ c
2. 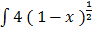 dx
dx
Let u = 1-x
du=-dx
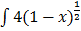 dx
dx
Let u = 1 – x
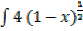 dx =
dx = 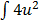 (- du )
(- du )
= -4 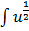 du
du
= 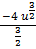 + c
+ c
=-4 x 
 + c
+ c
= 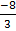
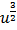 + c
+ c
= – 
 + c
+ c
3 
Let u= 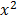 + 1
+ 1
du= 2xdx
dx = 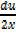
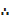
 =
= 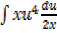
= 
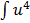 du
du
=  x
x 
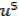 + c
+ c
= 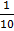
 + c
+ c
= 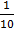
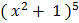 + c
+ c
Exercise
Determine the integral of each of the following
1. 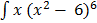 dx
dx
2. 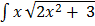 dx
dx
3. 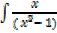 dx
dx
APPLICATION OF INTEGRATION
To determine the area under the curve
Given A is the area bounded by the curve y=f(x) the x -axis and the line x=0 and x=b where b> a
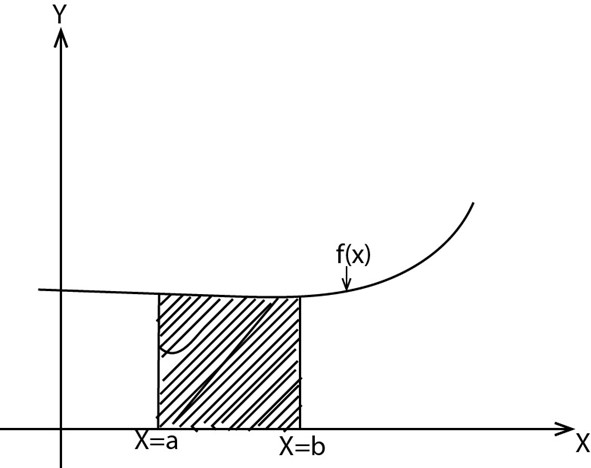
 The area under that curve is given by the define definite integral of f(x) from a to b
The area under that curve is given by the define definite integral of f(x) from a to b
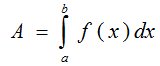
= f (b) – f (a)
Examples
1. Find the area under the curve f(x) =x2+1 from x=0 to x=2
2. Find the area under the curve f(x) = 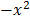 from x=1 to x=2
from x=1 to x=2
3. Find the area bounded by the function f(x) =x 2-3, x=0, x=5 and the x- axis
Solution
1. f(x) = 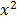 + 1
+ 1
y intercept=1
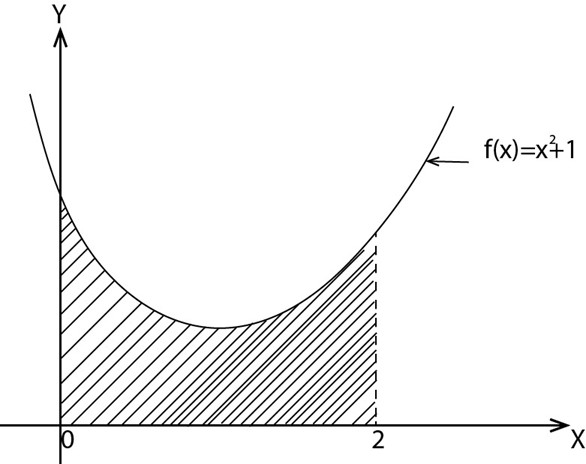
A = 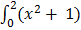 dx
dx
= 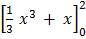
= (
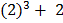 ) – (
) – (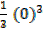 + 0)
+ 0)
= ( + 2) – (0)
+ 2) – (0)
= 4 or
or 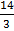 sq. units
sq. units
2. f(x)= 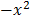
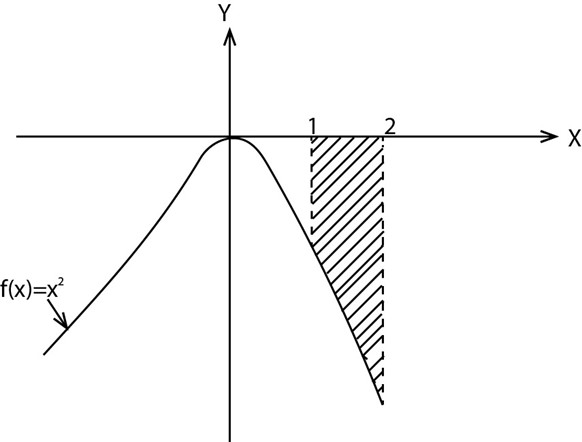
A = 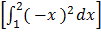
= 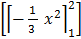
= 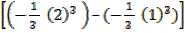
= 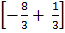 =
= 
=  sq.units
sq.units
3. f(x) = x2-3
Where: y intercept =-3
X intercept =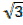 and x=
and x=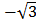
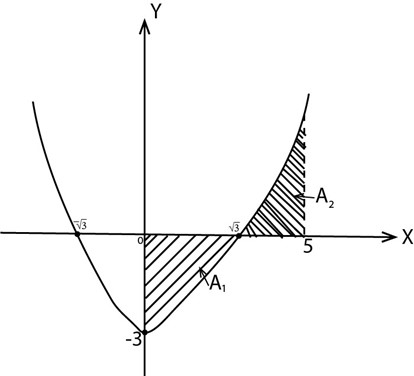
A = A1+A2
=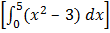 +
+ 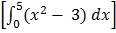
= 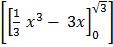 +
+ 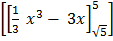
= 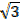 –
– 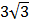 +
+ 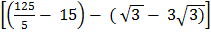
= 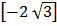 +
+ 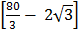
= 2 +
+ 
= 6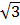 +
+ 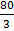 + 6
+ 6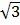
= 12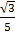 + 80 sq.units
+ 80 sq.units
EXERCISE
1. Find the area between y = 7-x2 and the x- axis from x= -1 to x=2
2. Find the area between the graph of y=x2 x – 2 and the x- axis from x= -2 to x=3
Solution
1. y =7-x2
Where y- intercept =7
X- Intercept =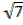
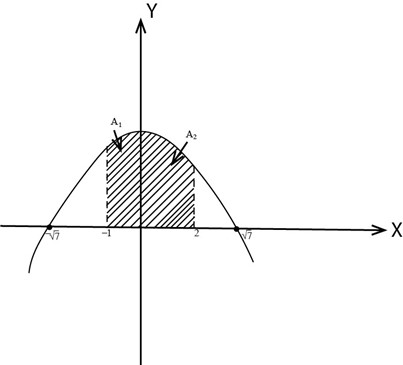
A = A1+A2
=  +
+ 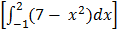
= 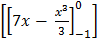 +
+ 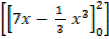
= (+6.67) + (11.3 – 0)
= + 6.67 + 11.3
=17.97 sq units
Volume of the Solids of Revolution
The volume,V of the solid of revolution is obtained by revolving the shaded portion under the curve, y= f(x) from x= a to x =b about the x -axis is given by
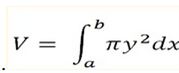
similarly, when the region is rotated about y- axis from y =a to y=b we shall have obtained the volume, V by
.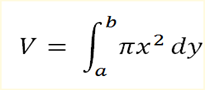
Example 1
Find the volume of revolution by the curve y=x2 from x=0 to x=2 given that the rotation is done about the the x- axis
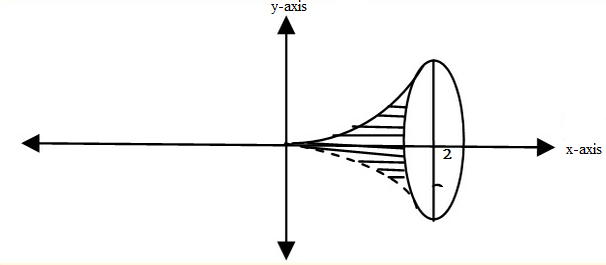
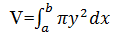
but y=x2
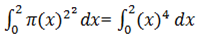
=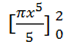
=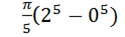
.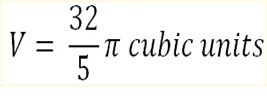
Exercise
1. Find the volume obtained when each of the regions is rotated about the x – axis.
a) Under y= x3, from x =0 to x=1
b) Under y2= 4-x, from x=0 to x=2
c)Under y= x2, from x=1 to x=2
d)Under y= √x, from x=1 to x=4
2. Find the volume obtained when each of the region is rotated about the y-axis.
a) Under y= x2, and the y-axis from x=0 to x=2
b) Under y= x3, and the y-axis from y=1 to y=8
c) Under y= √x, and the y-axis from y=1 to y=2
.