Definition
Is a branch of mathematics which enables one to solve problems which either the greatest or minimum/least value of a certain quantity is required under some given limitations or constraints.
Example
In a big – organization, decision about nglish-swahili/distribution” target=”_blank”>distribution in order to realize maximum profit or reduce costs of production are done by use of linear programming.
Limitation/ constraints are translated by linear inequalities.
Greatest value or least value will be expressed as a function (called the objective function)
Introduction
Drawing of linear inequalities
Example 01
Draw and show the half plane represented by 8x +2y ≥16
Solution
For 8x +2y ≥16; draw 8x + 2y = 16
For x – intercept, y = 0
8x = 16
X = 2
For y – intercept, x = 0
2y = 16
Y = 8
Using (0, 0) as a test point
8(0) +2(0) ≥ 16
0 ≥ 16 (False)

Example 02
Determine the solution set of the simultaneous inequalities
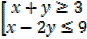
Solution
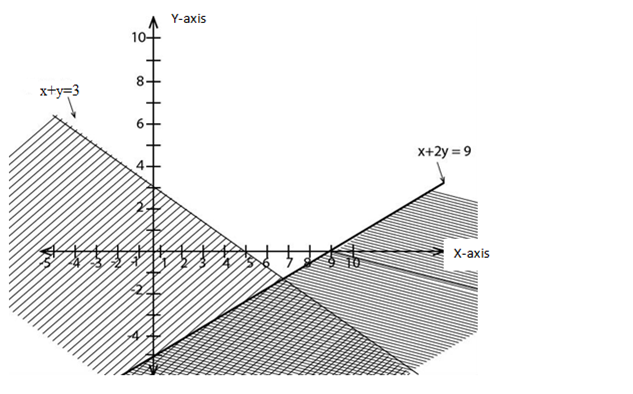
x + y ≥ 3 draw x + y = 3 (full line)
x + y = 3
At x – intercept y = 0 at y – intercept x = 0
x = 3 y = 3
For x – 2y ≤ 9, x – 2y = 9
At x – intercept y = 0 at y – intercept, x = 0
X =9 -2y = 9
Y = 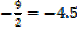
Using (0, 0) as a test point Using (0,0) as a test point
x + y ≥ 3 x – 2y ≤ 9
0 + 0 ≥ 3 0 – (2)(0) ≤ 9
0 ≥ 3 (F) 0 ≤ 9 (T)
The clear part is the solution set
The solution set is called the feasible region
Questions
Draw by shading unwanted regions of the half planes represented by following simultaneous inequalities
(i) y≥ 2x – 1, y ≤ -1
(ii) y≤ 2x – 1, y ≥ x – 3, y ≥ -1
(iii) y < 2x – 1, y ≤ -1
(iv) 6x + 9y ≥ 12
0.4x + 0.1y ≥ 0.2
32x + 10y ≥ 20
Evaluation of a function satisfied by the given set of inequalities
→Example
Find the maximum and minimum value of c = 4x + 3y + 38 subjected to
x + y ≥ 5
0 ≤ y ≤ 6 0 ≤ x ≤ 5
x ≥ 0, y ≥ 0
Solution
For x + y ≥ 5
x + y = 5
When x = 0, y = 5
y = 0, x = 5
For 0 ≤ y ≤ 6
0 = y = 6
Line y = 6
For 0 ≤ x ≤ 5
O = x = 5
Line x = 5
Test points x ≥ 0, shade left of x = 0
(0, 0) y ≥ 0, shade below of x = axis
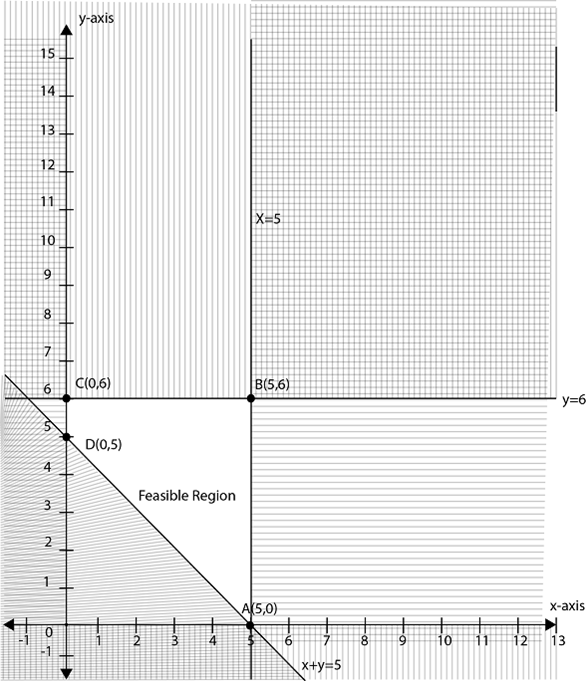
Corner points |
C = 4x + 3y + 38 |
| A (5, 0) | 4 (5) + 3 (0) +38 = 58 |
| B (5, 6) | 4 (5) + 3 (6) + 38 = 76 |
| C (0, 6) | 4 (0) + 3 (6) +38 = 56 |
| D (0, 5) | 4 (0) + 3 (5) + 38 = 53 |
edu.uptymez.com
: . The maximum value of c = 76 and occurs at (5, 6)
The minimum value of c = 53 and occurs at (0, 5)
Questions
1. Find the maximum and minimum values of the given functions and the value x and y where they occur
(i) Z = 4x + 3y
Subject to
x + 2y ≤ 10
3x + y ≤ 5
x ≥ 0, y ≥ 0
(ii) P = 134x + 20y
Subject to
x + y ≤ 160
10 ≤ x ≤ 60
0 ≤ y ≤ 120
(iii) T = 4x +7y
Subject to.
x + y ≤ 18
5 ≤ x ≤ 10
3 ≤ y ≤ 10
x ≥ 0, y ≥ 0
(iv) P = 2x + 4y
Subject to
2x + 3y ≥ 3
-5x + 4y ≤ 0
3x + 4y ≤ 18
X ≥ 0, y ≥ 0.