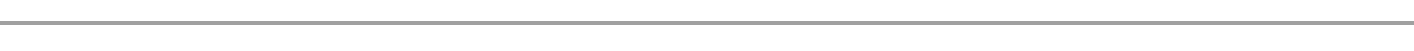BAM FORM 6 – LINEAR PROGRAMMING

Linear programming (Linear Optimization)

Linear programming (optimization) is the youngest branch of mathematics which was developed by George Dantizig in 1940’s. It is the model that consist of methods for solving many day to day life problems that in one way or the other demand the optimization of resources which are scarce.

The actual fact, linear programming is a mathematical procedure which helps to allocate, select, schedule and evaluate limited resources in the best possible way . These limited resources in this case may be money in the form of capital or costs. They can also be raw materials, labour and production equipments.

Generally, linear programming problems always are such that they tend to fulfill a linear statement of the form, mx + ny, called objective function. So if a₁x + b₁y ≤ c₁ and a₂x + b₂yc₂ are the only constraints that restrict the maximization of problems and if also x ≥ 0 and are their non – negativity constraints, then the standard way of reporting (writing) this problem is

            Maximize: m₁x + n₁y

            Subject to:     a₁x + b₁y ≤ c₁

                                    a₂x + b₂y ≤ c₂

                                    x ≥ 0

                                    y ≥ 0

     Similarly, if the problem is not of minimization of the objective function  m₅x ÷ n₅y and a₃x + b₃y ≥ c₃ while a₄x + b₄y ≥ c₄, x ≥ 0 and y ≥ 0 are  bounding constraints, then standard form is:

                        Minimize: m₅x + n₅y

                        Subject to:     a₃x + b₃y ≥ c₃

                                                a₄x + b₄y ≥ c₄

                                                 x  ≥ 0

                                     y  ≥ 0
Note:

1. An objective function is a mathematical statement that defines how best a data fits a particular assertion. It describes the essential characteristics of   the alternative          

2. Constraints are sets of inequalities for a linear programming problem in question, i.e a₁x + b₁y ≤ c₁, a₂x + b₂y ≤ c₂, x ≥ 0 and y ≥ 0 in the standard form for maximization given earlier.

 – If (x, y) happens to be one of the point that satisfies all the constraints, we call it a feasible solution. A set of all feasible solution form what we call a feasible region. The feasible region includes the boundary lines   (lines of equality). If the feasible region is enclosed by a polygon, it is said to be bounded or unbounded (see figure 11.5).

           

            If a feasible region has no point, the constraints involved are inconsistent and the problem does not have solution. The solution of any linear programming problem is given by one (some) of the feasible solution (s).However, these feasible solutions are many, which one should be taken as optimum solution? The following answer that

THEOREM

For a feasible region has no point of a linear programming which is bounded and not empty, the objective function attains either a maximum or a minimum value at the corner points (vertices) of the feasible region. If the feasible is unbounded, the objective function may or may not attain a minimum or maximum value, but if it attain, it does so at the corner points (vertices).

According to the theorem, the optimum solution comes the corner points, ie once you have graphed the constraints in Cartesian coordinate plane, test the corner points objective function, and then identify the optimum solution.

Example 11. 5

Siwatu wants to earn at least 13000/= this week. Her father has agreed to pay her 5000/= to know the lawn and 2000/= to weed the garden in a day suppose Siwatu mows the lawn once, what minimum number of days will she have to spend weeding the garden?

Solution

Let x and y be the number of days Siwatu spends moving the lawn and wedding the garden respectively.

Objective function x + y

For minimization

Subject to: 5000x + 2000y ≥ 13000

                        5x + 2y ≥ 13

Hence, she mows the lawns once, then

x ≥ 1 and x ≥0 y ≥ 0

Linear programming problems associated with this question is as follows

Minimize: x + y

Object to: 5x + 2y ≥ 13

                        x ≥ 1

                        x ≥ 0

                        y ≥ 0

The feasible region of the problem, together with the corner points are shown in figure the feasible region is indicated by shading.

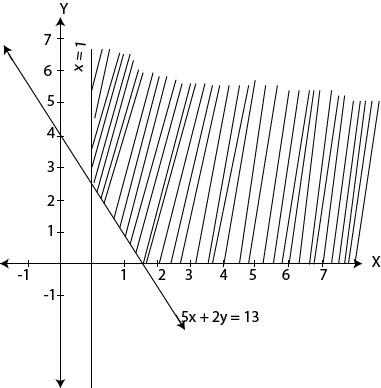
Table 11.4

                                    (5) Is the optimum solution row.

From table 11.4, the optimum solution is (1,4) meaning that to earn the required amount of money, Siwatu will have to work 4 days a week.

Example 11.6

A carpenter makes two kinds of furniture, i.e chairs and tables. Two operations M and N are used. Operation M is limited to 20 days a month while operations N are limited to 15 days per month. Table 11.5 shows the amount of time each operation takes for one chair and one table and the profit it makes on each item.

            Table 11.5

How many tables and chairs should the carpenter make in a month to maximize the income?

Solution

Let the number of chairs and tables be x and y respectively

Object function:

f(x,y) = 20000x + 24000y
2000x + 24000y

2x + 4y 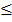 20

x + 2y ≤ 20

Also 3x + y ≤ 15

          x ≥ 0 and y ≥ 0

Thus, the linear programming problems associated with this question is as follow

Maximize: 20000x + 24000y

Subject to: x + 2y ≤ 10

                        3x + y ≤ 15

                       x ≥ 0

                        y ≥ 0

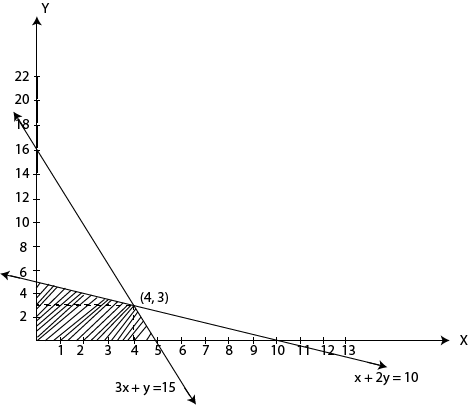
Figure shows the graph of linear programming problem given in example 11.6

Table 11.6

                                 152,000 is maximum value optimum solution row.                               

To maximize the income a month, a carpenter should make 4 chairs and 3 tables

Exercise 11.3

Answer each of the following questions as directed.

1.  a) Are the solutions of linear programming problems unique?                       

Explain

b) What do you understand by the terms    i) Feasible solutions?    ii) Feasible region?  iii) Constraints?    iv) Objective function?

2.   Maximize: 30x + 50y

            Subject to: 2x + 8y ≤ 60

                               4x + 4y ≤ 60 ,x ≥ 0

                                x ≥ 0

3.  Maximize: x + 6y

            Subject to: 5x + 10y ≤ 50

                                x + y ≤ 10

                                x ≥ 0

                                 y ≥ 0

4.  Minimize: 60 – (x + y)

            Subject to: x + y ≥ 3

                               x ≤ 4

                               x + 3y ≥ 15

                               x ≥ 0

                               y ≥ 0

5. Maximize a daily production of Mandazi and Chapati of mama Masawe’s business which is mixture of items M₁, and M₂. The required information is summarized in table 11.7           

Table 11.7

6. A farmer produces and sells onions and tomatoes. His profit being 150000/=and 100000/= respectively. His production involves two workers, M₁ and M₂ who are available for 100 days and 80 days a year respectively. M₁ works in union farms for 6 days in tomatoes farm for 10 days. M₂ works in onion farm for 4 days and in tomatoes farms for 4 days determine production costs that will maximize the production.

7. Mnazimmoja parking lot has a total area of 600M².A car requires 6 M²    and a bus 15 M² of space. The attendants can handle not more than 60  vehicles. If car is charged 2500/= and a bus 7500/=, how many of each should be accepted to maximize the profits? What is the of space left unused?

8. A bus contractor is contracted to transport 500 workers to their working places.For the contract, he has 3 type M buses capable of carrying 50 workers and 4 type N buses capable of carrying 85 workers each. Only     five drivers are available at the moment. If no bus is to repeat, how will the cost be reduced given that running type M bus costs 5000/= and type N bus costs 4000/=? How many drivers should be used?

9. Rose is a shopkeeper of Hilanyeupe. Shop in one occasion, she accepted goods with delivery note of a number of beef cans which was not visible enough. She trusted the supplier so she did not look at the delivery note and she did not bother herself counting. Two days later, she took the delivery note for the beef supplied two days ago and she found that the number was a three digits one with 4 as the middle digit. Owing to this, she concluded that the first digit can be less or equal to six (6) and the third digit can be smaller or equal to 6, and that the sum of the two unknown digits cannot exceed 8. If the difference of 6 times the first digit and the third” is to be big enough, what was the approximate number? (Assuming her conclusion was right)

Revision exercise 11

Solve each of the following graphically stating whether the system is inconsistent, consistent and independent or consistent and dependent.

1. 

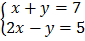
2. 

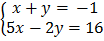
3.

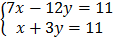
4. 

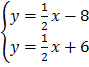
5.  

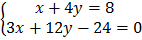
Solving each of the system of linear inequalities that follows

6. 

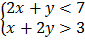
7.  

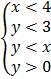
8. 

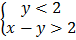
9. 

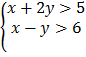
10.  

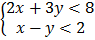
11. 

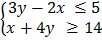
12. 

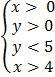
13.  Define the terms

            i) Linear programming

            ii) Bounded linear programming problem

            iii) Unbounded linear programming problem

14.  Maximize: x + 5y

            Subject to:

15. Minimize: 3x + 2y

            Subject to: 0≤ x ≤ 8

                                0 ≤ y ≤ 7

                                x + y ≤ 10

16.   Maximize 10x + 20y

            Subject to: 0< x <9

                               y > 18

                               x + 3y ≤ 75

17.  Maximize: 2500x + 7500

Subject to: x + y ≤ 60

                               x + 5y ≤ 100

                                x ≥ 0,  y ≥ 0

18.  Maximize: 120x + 250y

            Subject to: 0 ≤ x ≤ 300

                               0 ≤ y ≤ 200

                               2x + 3y ≤ 1200

19.A store manager of a certain company finds that he can store a batch of 3 machines in 2 m² and batch of 4 freezers in 4m². He reserved 160m²   altogether for this section of his stock and never allows the number of items to exceed 400. Find the greatest number of items he can accept subject to those conditions? If the machine is sold at 450000/= and a freezer at 225000/=, find the combination of items he should keep to maintain the greatest possible value of stock.

20.A company is intending to buy two equipments, E₁ and E₂, these equipments are to be used for a certain production. More information of these equipments is given in table 11.8

            Table 11.       

The company is prepared to buy at least E₂ equipment as E₁   equipments. At least 360 products must be produced per hour and up to 80m² of the floor space is available find the combination of the equipments that must be bought to maximize the profit will the floor space be left? If yes how much?

21. In a physics examination consisting of paper 1 (p₁) and paper 2 (p₂), both papers were marked out of 100. A candidate is given a mark x for p₁ and mark y for p₂. Someone is considered to have passed if 3x + 5y is at least 210, but candidates must score above 35 marks on p₁ and above 44 marks on p₂, Find the lowest value of x + y for any candidates who passes and give the corresponding values of x and y.