Logic concerns with the study of analysis of methods of reasoning which lead to certain conclusion or statement.
Example
If it rains today, we shall play football. It rained we did not play football
Simple and compound sentence
Consider the following sentence
i) The medians of a triangle meet at a point
ii) The diagonals of any quadrilateral are parallel
i) and ii) are simple sentence
iii) The median of a triangle meet at a point and the diagonal of a quadrilateral are parallel
iii) Is a compound sentence
Other connecting words are: or, but, while
TRUTH VALUE OF A SENTENCE
2 x 3 = 5 has a truth value ” false”
2 x 2 = 4 has a truth value ” True”
The number 23 is prime. “True”
Propositions
A proposition is any statement which is free from ambiguity and having a property, it is either true or false but not both nor neither.
Consider the following sentence;
i) Birds have no wings (p)
ii) The sun rises from the west. (p)
iii) 8 = 6 + 2 (p)
iv) The grass is green (p)
v) I am feeling hungry (not proposition)
TRUTH TABLE
A truth table is a matrix whose entries are truth values
E.g. F T Or T F
A complete truth for conjunction
Note: A conjunction is a compound proposition connected by the word “and”
E.g. the sun rises from the west and 8 = 6 + 2
The above proposition has a truth value false
The proposition having and/ but, if both of the sentence are true, then only truth value will be true.
The word “but” carries the same meaning as the word “and”
QUESTIONS
Find the components or simple sentence of the following conjunctions
a) 3< 5 and three are infinitely many prime numbers.
i) 3< 5
ii) There are infinitely many prime numbers
b) 4 is divisible by 2 and 4 is a prime number
i) 4 is divisible by 2
ii) 4 is a prime number
c) 2 < 3 and 5 < 3
i) 2< 3
ii) 5< 3
d) The sun rises from the west and  is irrational
is irrational
i) The sun rises from the west
ii) 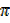 is irrational
is irrational
e) 2 is an odd number and it is false that 5 is even
A complete truth table for conjunction
Let P and Q be any general proposition
Required to find the truth table for P and Q
Now P and Q is written as P ∧ Q
P ∧ Q has truth value only when both P and Q are true
Truth table for P ∧ Q
Negation
A negation is a sentence which has an opposite truth value to the given one
– One way of forming a negation is to put the word ” not” with a verb
Example: 6 is divisible by 3
6 is not divisible by 3
It is not true that 6 is divisible by 3
It is false that 6 is divisible by 3
Given a statement P, its negation is denoted 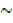 P
P
The complement of ~ P is P
Truth Table for negation
Disjunction
Another word used to combine sentence is the word ” or “
Consider the sentence
i) 43 < 3 ii) 5 > 3
– combining them with the word ” or ” i.e. 43 < 3 or 5 > 3
– The connective word ” or ” is called a disjunction and is symbolized by ” V “
The truth value for disjunction is only false when both the components are false
If P and Q are statement,then P or Q is symbolized as P V Q
P V Q has a truth value false in one case when both P and Q are false
Truth Table for disjunction
Implications
These are statements of the form ” if……..then……”
Example. If a quadrilateral is a parallelogram then the pair of opposite sides are parallel
The phrase “a quadrilateral is a parallelogram” called hypothesis or antecedent
The phrase “the pair of opposite sides are parallel” is called a conclusion or constituent
If P 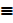 hypothesis
hypothesis
Q 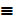 conclusion
conclusion
Then the statement if P then Q its implication in short we write P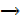 Q
Q
Consider the statement
If 43 < 3 then 5 > 3 T
If 43 < 3 then 5 < 3 T If hypothesis is T and conclusion is F 43 > 3 then 5 < 3 F then the implication is T
→Note: The compound statement P → Q is false only in one case P is true and Q is false.
Truth Table for P 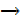 Q
Q
Propositions which carry the same meaning as if P then Q
i) If P, Q
ii) Q if P
iii) Q provided that P
iv) P only if Q
v) P is a sufficient condition for Q
vi) Q is a necessary condition for P
EXERCISE
1. Determine the truth values of the following
a) If 2 < 3 then 2 + 3 = 5 T
b) If 3 < 2 then 3 + 2 = 5 T
c) If 2 + 3 = 5 then 3 < 2 F
d) If 2 + 1 = 2 then 1 = 0 T
2. Find the components of the following compound
i) If 3 < 5 then 10 + m = 9
a) 3 < 5
b) 10 + m = 9
ii) a + b = c + d only if p + q = r2
a) a + b = c + d
b) p + q = r2
iii) If Galileo was born before Descartes then Newton was born before Shakespeare
a) Galileo was born before Descartes
b) Newton was born before Shakespeare
3. Write a truth table for
i) (P ∧ Q) V (P V Q) ii) (P → Q) ∧ P iii) ((P → Q) → Q)
Solutions
i) (P ∧ Q) V (P V Q)
ii) (P → Q) ∧ P
iii) ((P → Q) → Q)
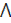 Q
Q