LAWS OF ALGEBRA OF PROPOSITIONS
1. Idempotent laws
a) P V P 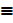 P
P
b) P Λ P 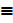 P
P
2. Commutative
a) P V Q 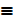 Q V P
Q V P
b) P 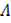 Q
Q  Q Λ P
Q Λ P
3. Associative laws
a) (P V Q) V R  P V (Q V R)
P V (Q V R)
b) (P Λ Q) Λ R  P Λ (Q Λ R)
P Λ (Q Λ R)
4. Distributive laws
a) P V (Q Λ R) 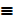 (P V Q) Λ (P V R)
(P V Q) Λ (P V R)
b) P Λ (Q V R)  (P Λ Q) V (P Λ R)
(P Λ Q) V (P Λ R)
5. Identity laws
a) P V f 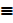 P
P
b) P Λ t 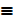 P
P
c) P V t 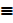 t
t
d) P Λ f  f
f
6. Complementary laws
a) P V ~ P 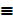 t
t
b) P Λ ~ P 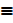 f
f
c) ~ ~P 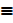 P
P
d) ~ T 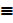 F or t~
F or t~ f
f
e) ~ F 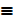 T or f~
T or f~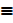 t
t
7. De-Morgan’s law
a) ~ (P V Q) 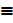 ~ P Λ ~ Q
~ P Λ ~ Q
b) ~ (P Λ Q) 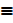 ~ P V ~ Q
~ P V ~ Q
Examples
Using the laws of algebra of proposition simplify (P V Q) ∧ ~ P
Solution
(P V Q) Λ ~ P 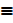 (~ P Λ P) V (~ P Λ Q) ……distributive law
(~ P Λ P) V (~ P Λ Q) ……distributive law
 f V (~ P Λ Q) ………compliment law
f V (~ P Λ Q) ………compliment law
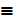 (~ P Λ Q) ………..identity
(~ P Λ Q) ………..identity
Questions
1. Simplify the following propositions using the laws of algebra of propositions
i) ~ (P V Q) V (~P Λ Q)
ii) (P Λ Q) V [~ R Λ (Q Λ P)]
2. Show using the laws of algebra of propositions (P Λ Q) V [P Λ (~Q V R)] 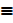 P
P
3. Construct a truth table for [(p → ~q) ∧ (r → p) ∧ r] → ~p
SENTENCE HAVING A GIVEN TRUTH TABLE
Example.1 Find a sentence which has the following truth table
Step: 1. Mark lines which are T in last column
2. Basic conjunction of P and Q
3. Required sentence is the disjunctions of the above basic conjunction
Required sentence (P ∧ Q) V (P ∧ ~ Q) V (~ P ∧ Q)
Example. 2
Find a sentence having the truth table below
Solution
| P | Q | R | – | Basic conjunction |
| T | T | T | T | P ∧ Q∧ R |
| T | T | F | F | |
| T | F | T | F | |
| T | F | F | T | P ∧ ~ Q ∧ ~ R |
| F | T | T | F | |
| F | T | F | F | |
| F | F | T | F | |
| F | F | F | F |
edu.uptymez.com
Required sentence is (P ∧ Q ∧ R) V (P ∧ ~ Q ∧ ~ R)
Example. 3
Find a sentence having the following truth table and simplify it.
SOLUTION
The required sentence is (P ∧ Q) V (~ P ∧ Q) V (~ P ∧ ~ Q)
To simplify;
(P ∧ Q) V (~P ∧ Q) V (~P ∧ ~Q) = (P ∧ Q) V [~P ∧ (Q V ~Q)…..distributive law
= (P ∧ Q) V [~ P ∧ t] ……compliment law
= (P ∧ Q) V [~ P] ……..identity
= (P V ~P) ∧ (~P V Q)…….. Distributive
= t ∧ (~P V Q) ………compliment
= (~P V Q) ………identity
Note
P → Q ≡ ~ P V Q
QUESTIONS
1. for each of the following truth tables (a), (b) and (c) construct a compound sentence having that truth table.
| P | Q | R | (a) | (b) | (c) |
| T | T | T | T | T | F |
| T | T | F | F | T | T |
| T | F | T | T | T | T |
| T | F | F | F | T | F |
| F | T | T | F | F | F |
| F | T | F | F | F | F |
| F | F | T | F | F | F |
| F | F | F | F | F | T |
edu.uptymez.com
Solution
| P | Q | R | (a) | (b) | (c) | Basic conjunction of (a) | Basic conjunction of (b) | Basic conjunction of ( c) |
| T | T | T | T | T | F | P ∧ Q ∧ R | P ∧ Q ∧ R | |
| T | T | F | F | T | T | P ∧ Q ∧ ~ R | P ∧ Q ∧ ~ R | |
| T | F | T | T | T | T | P ∧ ~ Q ∧ R | P ∧ ~ Q ∧ R | P ∧ ~ Q ∧ R |
| T | F | F | F | T | F | P ∧ ~Q ∧ ~ R | ||
| F | T | T | F | F | F | |||
| F | T | F | F | F | F | |||
| F | F | T | F | F | F | |||
| F | F | F | F | F | T | ~ P ∧ ~ Q ∧ ~ R |
edu.uptymez.com
→The required sentence for (a) is (P ∧ Q ∧ R) V (P ∧ ~ Q ∧ R)
→The required sentence for (b) is (P ∧ Q ∧ R) V (P ∧ Q ∧ ~R) V (P∧ ~Q ∧ R) V (P ∧ ~Q∧ ~ R)
→The required sentence for (c) is (P ∧ Q ∧ ~R) V (P ∧ ~Q ∧ R) V (~P ∧ ~Q ∧ ~R)
2. i) construct a truth table for ~ (P → Q)
ii) Write a compound sentence having that truth table (involving ~, ∧ , v)
3. Repeat for the following sentence
i) ~ P → ~Q ii) ~ p  Q
Q
More
question
1. Find a compound sentence having components P and Q which is true and only if exactly one of its components P, Q is true.
2. Find a compound sentence having components P, Q and R which is true only if exactly two of P, Q and R are true.
3. Give an example of sentence having one component which is always true
4. Give an example of a compound sentence having one component which is always false
5. Use laws of algebra of propositions to simplify ~ (p V q) ∧ (~ p ∧ q)
6. Show that p 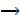 q and ~ p v q are logically equivalent
q and ~ p v q are logically equivalent
7. If Apq 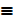 p ∧ q and Np
p ∧ q and Np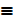 ~ p write the following without ~ and A
~ p write the following without ~ and A
i) ~ (p ∧ q)
ii)~ (p ∧ ~q)
iii) ~ (~ p ∧ q)
iv) ~ (p ∧ ~ q)
QUESTIONS
1. Rewrite the following without using the conditional
i) If it is cold, he wears a hat
ii) If productivity increases, then wages rise
2. Determine the truth value of the following
i) 2 + 2 = 4 if and only if 3 + 6 = 9
ii) 2 + 2 = 4 if and only if 5 + 1 = 2
iii) 1 + 1 = 2 if and only if 3 + 2 = 8
iv) 1 + 2 = 5 if and only if 3 + 1 = 4
3. Prove by truth table
i) ~ (p  q) ≡ p
q) ≡ p 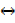 ~q
~q
ii) ~ (p 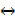 q) ≡ ~ p
q) ≡ ~ p 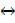 q
q
4. Prove the conditional distributes over conjunction i.e.
[p → (q ∧ r)] ≡ (p → q) ∧ (p → r)
5. Let p denote ” it is cold” and let q denote ” it rains “. Write the following statement in symbolic form
i) It rains only if it is cold.
ii) A necessary condition for it to be cold is that it rains.
iii) A sufficient condition for it to be cold is that it rains
iv) It never rains when it is cold.
6. a) Write the inverse of the converse of the conditional
” If a quadrilateral is a square then it is a rectangle”
b) Write the inverse of the converse of the contra positive of
“If the diagonals of the rhombus are perpendicular then it is a square”