LOGICAL IMPLICATIONS
A proposition P is said to be logically imply a proposition Q if p → Q is a tautology
Example
Show that p logically implies p v q
Solution; Construct a truth table for p → (p v q)
Since column 4 is a tautology then p logically implies p v q
ARGUMENTS
An argument in logic is a declaration that a given set of proposition p1, p2, p3….pn called premises yields to another proposition Q called a conclusion such as argument is denoted by p1, p2….pn
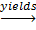 Q
Q
Example of an argument
If I like mathematics, then I will study, either I study or I fail. But I failed therefore I do not like mathematics.
VALIDITY OF AN ARGUMENT
Validity of an argument is determined as follows
→An argument P1, P2, P3… Pn 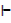 Q is valid if Q is true whenever all the premises P1, P2, P3… Pn are true
Q is valid if Q is true whenever all the premises P1, P2, P3… Pn are true
→Validity of an argument is also determined if and only if the proposition (P1
∧ P2
∧ P3
∧ ….. Pn) → Q is a tautology
Example
Prove whether the following argument is valid or not P, P → Q 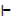 Q
Q
Solution:
Draw a truth table for [P ∧ P → Q] → Q
1. Since in row 1 the conclusion is true and all the premises are true then the argument is valid
2. Since column 5 is a tautology then the argument is valid
QUESTION
Use the truth table to show whether the given argument is valid or not
P → Q, Q → R 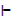 P → R
P → R
Example
Symbolize the given argument and then test its validity
*If I like mathematics, then I will study, either I study or I fail. But I failed, therefore I do not like mathematics.
Solution.
The given argument is symbolized as follows
Let p ≡ I like mathematics
q ≡ I will study
r ≡ I fail
Then given argument is as follows
P → q, q v r, r, 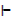 ~p
~p
Testing the validity
[(p → q) ∧ (q ∧ r)∧ r] → ~p
| P | Q | r | P → q | q v r | 3 ∧ 4 ∧ 5 | ~ p | 6 → 7 |
| T | T | T | T | T | T | F | F |
| T | T | F | T | T | F | F | T |
| T | F | T | F | T | F | F | T |
| T | F | F | F | F | F | F | T |
| F | T | T | T | T | T | T | T |
| F | T | F | T | T | F | T | T |
| F | F | T | T | T | T | T | T |
| F | F | F | T | F | F | T | T |
edu.uptymez.com
Since column 8 is not a tautology the given argument is not valid
QUESTIONS
1. Translate the following arguments in symbolic form and then test its validity
i) If London is not in Denmark, then Paris is not in France. But Paris is in France, therefore London is in Denmark
ii) If I work I cannot study. Either I work or I pass mathematics. I passed mathematics therefore I studied.
iii) If I buy books, I lose money. I bought books, therefore I lost money
2. Determine the validity of
i) p → q, ~q 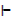 ~p
~p
ii)~p → q, p 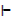 ~q
~q
iii) [p → ~ q], r → q, r 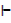 ~p
~p
ELECTRICAL NETWORK
Electrical network is an arrangement of worse and switches that will accomplish a particular task e.g. lighting a lamp, turning a motor, etc
The figure below shows an electrical network
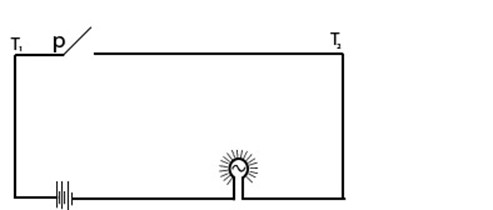
When the switch p is closed the current flows between T1 and T2
The above network simplifies to the following network
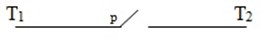
Relationship between statement in logic and network

A SERIES AND PARALLEL CONNECTION OF SWITCHES
A series connection of switches
The following switches are connected in series
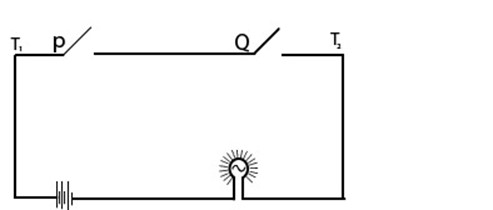
The current flow between T1 and T2 when both switches are closed current flows when p ∧ Q is true
A parallel connection of switches
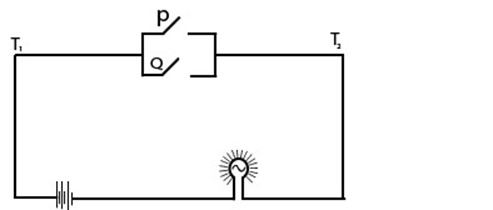
The current will flow when either one of the switches is closed.
Currents flow when P V Q is true
Example
Consider the electrical network below
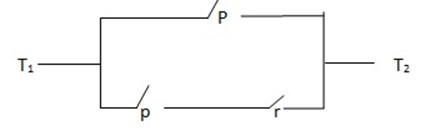
i) Construct a compound statement presenting the network above
ii) Find possible switch setting that will allow the current to flow between T1 and T2
Solution
Note i) current flows between T1 and T2 when switch p is closed i.e. p is true OR
ii) The current flows between T1 and T2 when switch switches q and r are closed i.e. Q ∧ R is true.
The required compound statement is p v (Q ∧ R)
iii) To find possible switch setting, draw a truth table P v (Q ∧ R)
| P | Q | R | Q ∧ R | P V (Q ∧ R) | Current flows yes or No |
| T | T | T | T | T | Yes |
| T | T | F | F | T | Yes |
| T | F | T | F | T | Yes |
| T | F | F | F | T | Yes |
| F | T | T | T | T | Yes |
| F | T | F | F | F | No |
| F | F | T | F | F | No |
| F | F | F | F | F | No |
edu.uptymez.com
Possible switch setting
| P | Q | r |
| Closed | Closed | Closed |
| Closed | Closed | Closed |
| Closed | Closed | Closed |
| Closed | Closed | Closed |
| Closed | Closed | Closed |
edu.uptymez.com
Questions
1. Construct compound statement that correspond to the networks
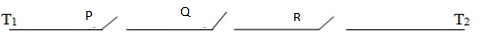
Solution
The current will flow when all three switches p, q, and r are closed i.e. p ∧ q ∧ r
The required compound statement is P ∧ Q ∧ R
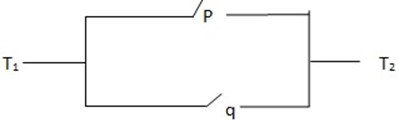
The required component statement is (P ∨ q)
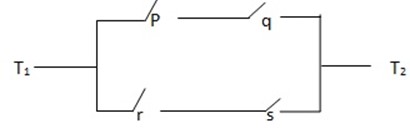
The required compound statement is (p ∧ q) V (r∧ s)
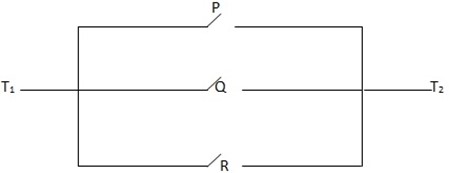
The required compound statement is P V Q V R
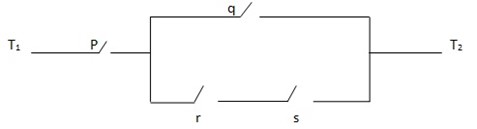
The required compound statement is p ∧ (q V (r ∧ s))
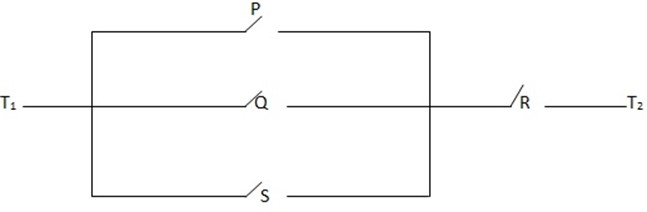
The required compound statement is (P ∨ Q ∨ R) ∧ S
2. In electrical network of (ii) find possible switch setting that will allow the current to flow between T1 and T2
ii) (P ∨ Q) ∧ R
| P | Q | R | P V Q | (P V Q) ∧ R |
| T | T | T | T | T |
| T | T | F | T | F |
| T | F | T | T | T |
| T | F | F | T | F |
| F | T | T | T | T |
| F | T | F | T | F |
| F | F | T | F | F |
| F | F | F | F | F |
edu.uptymez.com
Possible switch settings
From statements to network
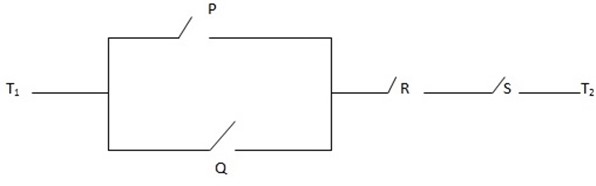
Example
Draw a network for the statement (p v Q) ∧ (R ∧ S)
Solutions
Corresponding network is shown below
Questions
Draw network for the following statements
1. [P ∨Q ∧ (R ∧ S)]
2. [(P ∧ Q) ∧ (R V S)]
3. [P V (Q ∧ S) V (R ∧ T)]
4. (Q V(R V S) V P)
5. [P V (Q ∧ (R ∧ S)]
COMPLEX SWITCHES
These operates as follows
i) When one switch is closed, the other one closes also
ii) When one switch is closed, the other one opens
Refers to the diagram
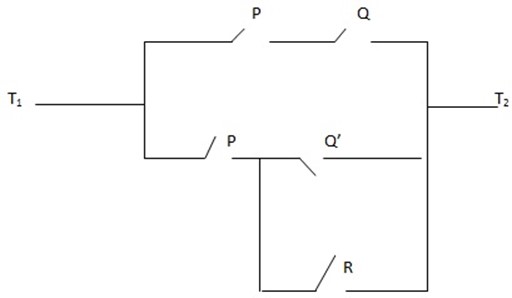
The compound relating to flow of electrical current is given
(P ∧ Q) V [P ∧ (~ Q V R)]
To find possible switch setting that will allow the current to flow between T1 and T2
– Draw a truth table for (P ∧ Q) V [ P ∧ ( ~ Q V R)]
1 2 3 4 5 6 7 8
| P | Q | R | P ∧ Q | ~ Q | ~ Q V R | P ∧ (~ Q V R) | 4 V 7 |
| T | T | T | T | F | T | T | T |
| T | T | F | T | F | F | F | T |
| T | F | T | F | T | T | T | T |
| T | F | F | F | T | T | T | T |
| F | T | T | F | T | F | F | F |
| F | T | F | F | F | F | F | F |
| F | F | T | F | T | T | F | F |
| F | F | F | F | T | T | F | F |
edu.uptymez.com
Possible switch setting
Example
Without using a truth table draw a sample network for the statement
(P ∧ Q) V [ P ∧ (~ Q V R)]
Solution
(P ∧ Q) V [ P ∧ (~ Q V R) ] = P ∧ (Q V (~ Q V R) ….. distributive
= P ∧ (Q V ~ Q) V R ……. associative
= P ∧ (t V R) ….. Complement
= P ∧ t ….. Identity
= P ….. Identity
The statement simplifies to p
The corresponding network is a follows
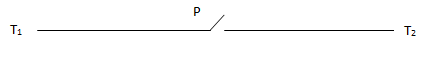
For a statement which on simplifying ends upon F network drawn is as follows

For a statement which upon simplifying yields to T, network is drawn as follows

QUESTION
1. For each of the network shown below. Find a compound statement that represents it
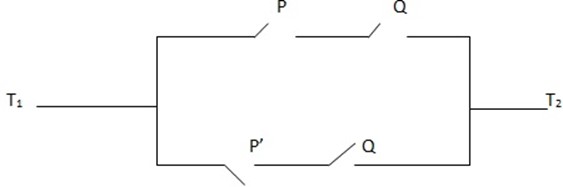
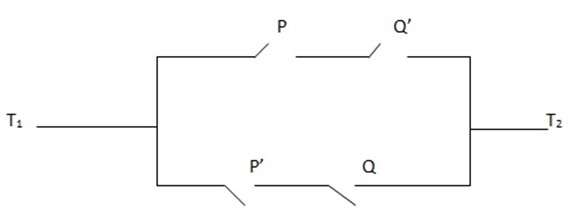
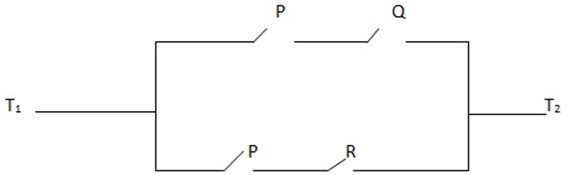
2. (a) Draw network for the corresponding statement
i) (P ∧ ~ Q) ∨ (Q ∧ P)
ii) (P ∧ ~ Q) ∨(Q ∧ ~ R)
iii) P → Q ≡ ~ P ∨ Q
iv) (P → Q) ∧ (p v Q) ≡ (~ P V Q) ∧ (P V Q)
(b) Simplify the statement in 2 (iv) using the laws of algebra of propositions and draw a simple network