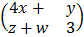is an arrangement of number in rows and columns. Its usually denoted using capital letters
E.g A = 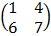 B =
B = 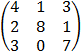 C =
C =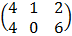
Order: A matrix is said to be of order m x n if it has m rows and n columns.
E.g. Order of A is 2 x 2
Order of B is 3 x 3
Order of C is 2 x 3
Types
– Rows matrix is a matrix with only one row.
e.g. D = (2 1 6)
– Column matrix is a matrix with only one column.
E.g. Д = 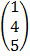
– Square matrix is a matrix with equal number of rows and column
E.g. A = 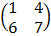 B =
B = 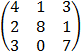
– Identity matrix (T) is a square matrix with all elements in the leading diagonal equals to 1 and the rest are 0.
E.g. I = 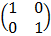
I = 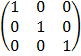
Property
AI = A
Null (zero) matrix (Z) is a matrix with all elements equation to 0 e.g. Z = 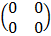
Properties
1) A + Z = A
2) AZ = Z
Operations
i) Addition/ subtraction
This is only possible if the matrices have the same order
E.g. A = 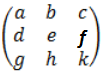 B =
B = 
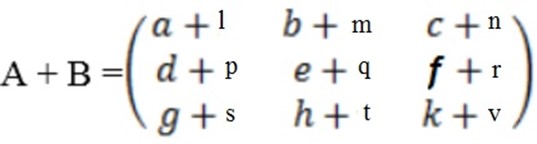
ii) Scalar multiplication
Given a scalar multiplication then
A = t 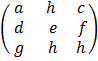
= 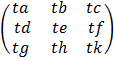
E.g.: Evaluate tP – sQ
Given t = 3 s = ½, P = 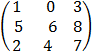
Q = 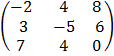
Solution
tP – SQ
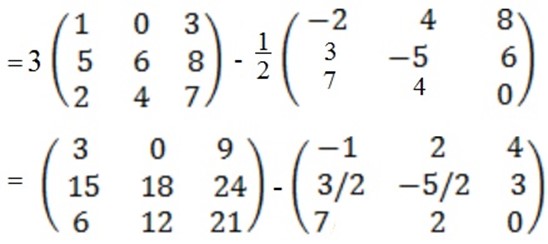
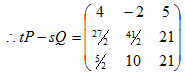
iii) Product
AB is only possible if the order of A is m x n and that of B is n x p and the resulting matrix will be of the order m x p.
e.g. i) 
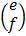
2 x 2 2 x 1
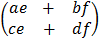
ii) 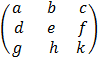
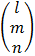
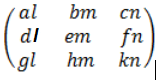
E.g. 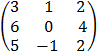
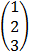
3 x 3 3 x 1
= 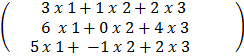
= 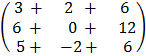 =
= 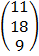
iv) 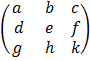
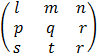
3 x 3 3 x 3
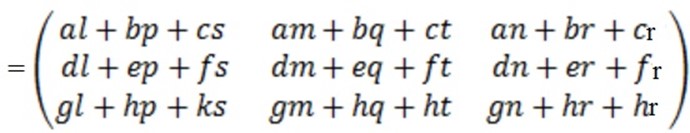
E.g. 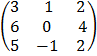
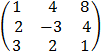
3 x 3 3 x 3
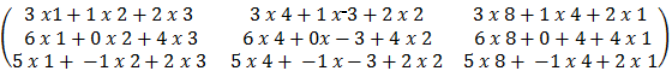
=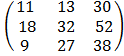
Determinant of a 2 x 2 matrices
Given A =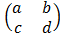
Determinant of A = 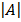
= 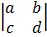
= ad – cb
If the determinant A = 0 then A is singular matrix
E.g. which of the following is singular or non singular matrix
A = 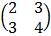
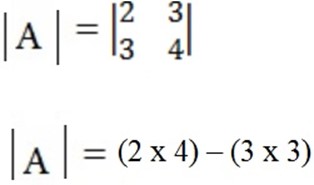
8 – 9 = -1 Non – singular matrix
B = 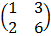
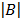 = 1(6) – 2(3)
= 1(6) – 2(3)
= 6 – 6
= 0 Singular matrix
C = 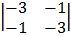
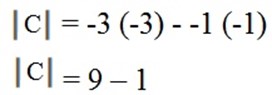
= 8 Non – singular matrix
Inverse of a 2 x 2 matrix
Given A = 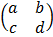
The inverse of A = A-1
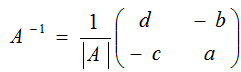
E.g. A = 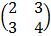
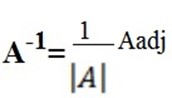
 = 2 (4) – 3(3) = -1
= 2 (4) – 3(3) = -1
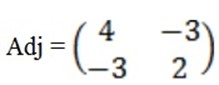
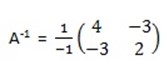
A-1 =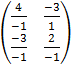
A-1 =
Solving system of simultaneous equations in 2 unknowns
Given the following equations
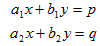
In a matrix form
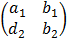
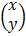 =
= 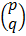
Determinant method
1. (Cramer’s rule)
Solving for x
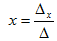 where
where
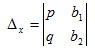 and
and 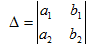
Solving for y
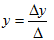 where
where
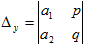 and
and 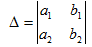
E.g. solving the following using Cramer’s rule
x + y = 3
x – y = 1
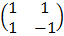
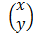 =
= 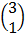
A= 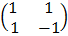 Δ =
Δ =
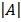 = 1 (-1) – (1)= -2
= 1 (-1) – (1)= -2
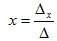 where
where 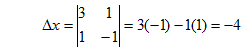
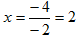
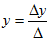
Δ =
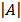 = 1 (-1) – (1)= -2
= 1 (-1) – (1)= -2
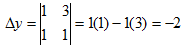
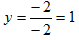
 =
= 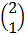
2. Inverse method
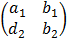
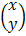 =
= 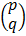
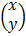 = A-1
= A-1 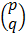
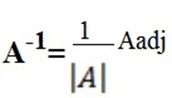
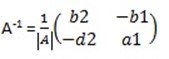
E.g. x + y = 3
x – y = 1
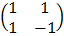
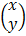 =
= 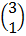
A = 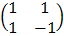
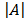 = -1(1) – 1 (1) = -2
= -1(1) – 1 (1) = -2
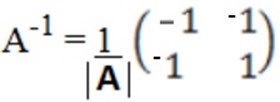
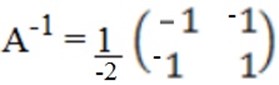
A-1 = 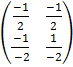
A-1 = 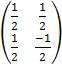
 =
= 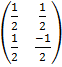
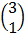
= 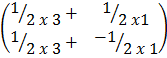
= 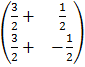
= 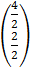
= 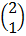
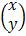 =
= 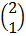
Determinant of a 3 x 3 matrix
Given A = 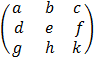
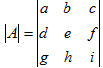
= a 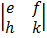 – b
– b 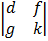 + c
+ c 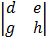
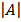 = a (ek – fh) – b (dk – fg) + c (dh – eg)
= a (ek – fh) – b (dk – fg) + c (dh – eg)
E.g Find 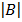 given B =
given B = 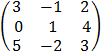
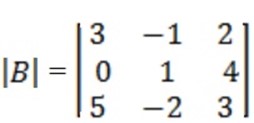
= 3 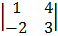 – (-1)
– (-1) 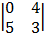 + 2
+ 2 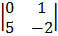
= 3 (3 + 8) + 1(0 – 20) + 2 (0 – 5)
= 33 – 20 – 10
= 3
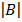 = 3
= 3
Transpose


E.g, B = 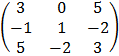
BT = 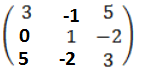
Co factors
A =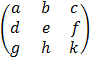
A co factor of an element in a 3 x 3 matrix is given by determine determinant of a 2 x 2 matrix which is formed by removing elements in the same row and column with given element and multiply by 1 or -1 according to the following procedure.
Produce 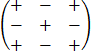
E.g. C = 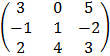
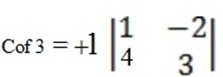
= (3 + 8) = 11
Cof 0 -1 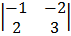
= -1 (-3 + 4) = -1
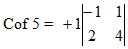
= + (-4 – 2) = -6
Cof (-1) -1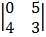
= -1 (0 – 20) = 20
Cof 1 + 1 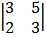
= 1 (9 – 10) = -1
C0f -2
-1 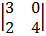
= -1 (12 – 0) = -12
Cof 2
1 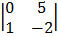
= 1 (0 – 5) = -5
Cof 4
-1 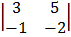
= -1 (-6 + 5) = 1
Cof 3
1 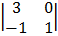
= 1 (3 + 0) = 3
Matrix of Cofactors
A = 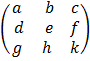
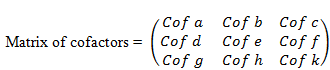
Adjoin of A = adj, AT = the transpose of matrix of Cofactors
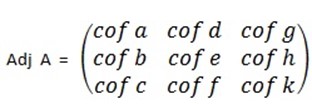
Inverse of A
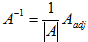
Summary
Procedure for finding inverse of a 3 x 3 matrices
i) Find the determinant
ii) Find the cofactors
iii) Form the matrix of cofactors
iv) Form the adjoint
v) Find the value
Solving simultaneous equation in 3 unknown
1. Determinant method (Cramer’s rule)
Given that a1x + by + c1z = p
a2x + b2y c2z= q
a3x + b3y c3z = r
In a matrix form we have
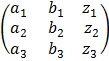
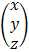 =
= 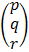
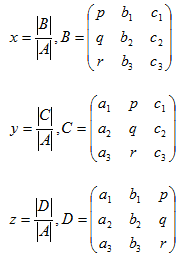
E.g. using Cramer’s rule Solve x + 2y + z = 6
2x + y – z = 3
3x – y + 2z = 5
Solution
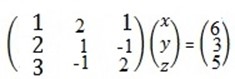
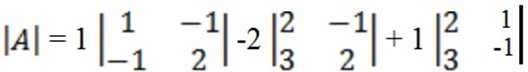
= 1 (2 – 1) – 2 (4 + 3) + 1 (-2 – 3)
= 1 – 14 + -5 = -18

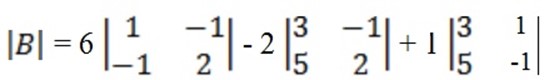
= 6 (2 – 1) – 2 (6 + 5) + 1 (-3
= 6 – 22 + – 8
 = -24
= -24
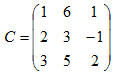
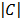 = 1
= 1 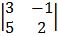 – 6
– 6 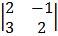 + 1
+ 1 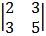
= 1 (6 + 5) – 6 (4 + 3) + 1 (10 – 9)
= 11 – 42 + 1
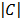 = -31 + 1 = -30
= -31 + 1 = -30
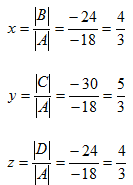
II. Inverse method
a1x + b1y + c1z = p
a2x + b2y + c2z = q
a3x + b3y + c3z = r
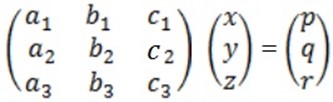
A 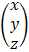 =
= 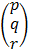
AA-1
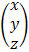 = A-1
= A-1
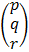
I 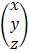 = A-1
= A-1
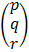
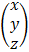 = A-1
= A-1
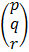
E.g: solving using inverse method
x + 2y + z
= 6
2x + y – z = 3
3x – y + 2z = 5
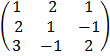
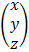 =
= 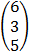
A =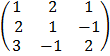
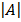 = 1
= 1 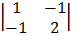 – 2
– 2 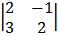 + 1
+ 1 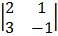
= 1 (2 – 1) – 2 (4 + 3) + 1 (-2 – 3)
= 1 – 14 + (-5)
= -13 – 5
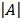 = -18
= -18
A = 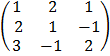
Cof 1 = + 1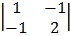 cof 2 = -1
cof 2 = -1 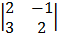
= +1 (2 – 1) = 1 (4 + 3)
= 1 = -7
Cof 1 = + 1 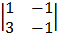 cof 2 = -1
cof 2 = -1 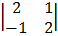
= + (-2 – 3) = -1 (4 + 1)
= -5 = -5
Cof 1: + 1 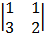 cof -1 = -1
cof -1 = -1 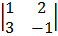
= +1 (2 – 3) = -1 (-1 – 6)
= -1 = 7
Cof 3: + 1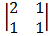 cof -1= -1
cof -1= -1 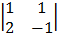
= + 1 (-2 – 1) = -1 (-1 – 2)
= -3 = 3
Cof 2: + 1 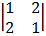
= + 1 (1 – 4)
= -3
Matrix of cofactors, C
C = 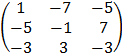
Note: Adj A = CT
Adj A = 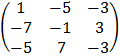
Inverse of A
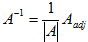
A-1 = 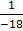
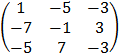
A-1 =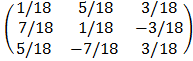
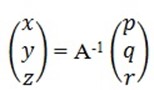
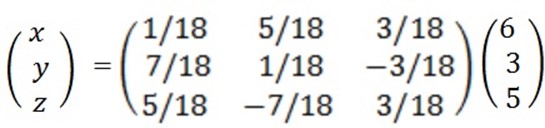
= 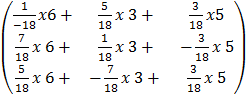
= 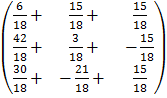
= 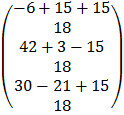 =
= 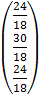
= 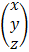 =
= 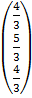
Exercise
1. a) Given A = 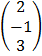 , and B =
, and B = 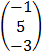 , Find A + B
, Find A + B
b) If A = 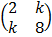 is singular find the value of k
is singular find the value of k
c) Find the inverse of B = 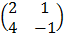
d) Solve 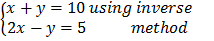
2. Using i) Determinant
ii) Inverse, solve for x, y and z
3x – y + z = 2
x + 5y + 2z = 6
2x + 3y + z
= 0
3. a) solve
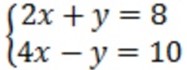
i) Using determinant
ii) inverse
b) If A =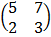 , B =
, B = 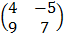 and
and
C = 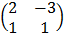
Show that (A + B – 2C) is singular
c) Solve x + y + z
= 6
3x – 2y – z
= -1
2x + 4y + 3z = 19 Using i) determinant
ii) Inverse
4. Solve, 2x – 3y + z = 3
-x + 4y + 3z = 16
3x + 2y – 2z = 1
5. A transformation is given by the matrix M where M = 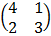 Find the (a) image of (-2, 5) under M (b) Inverse of M.
Find the (a) image of (-2, 5) under M (b) Inverse of M.
6. If T is linear transformation such that T = 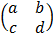 and T (x, y) = (3y, 5x), Find T hence evaluate T (1, 2)
and T (x, y) = (3y, 5x), Find T hence evaluate T (1, 2)
b) Use inverse method to solve
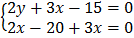
7. a) Given A = 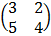 . B =
. B = 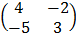 , Find AB and BA
, Find AB and BA
b) Find the value of x,y,w and z
3 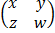 =
= 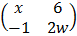 +
+