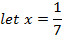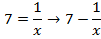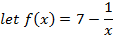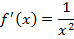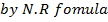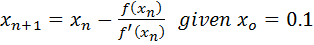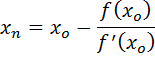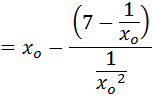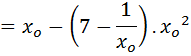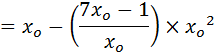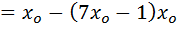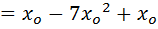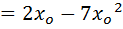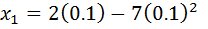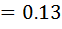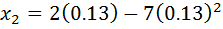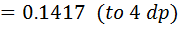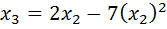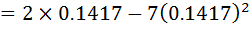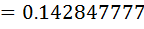Introduction
Numerical methods can be used to find roots of a function
→We find roots of a function by;
1. Direct method
2. Iterative method
ERROR
An error can be defined as the deviation from accuracy or correctness
Error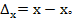 
Where;
X = is the exact value of a number
X0 = is an approximate value of a number
Example
If X0 = 3.14 and x=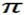 
then
.
= 
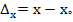
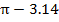
=0.001592654
TYPES OF ERROR
A) Systematic error
This is a predictable error or constant caused by imperfect calibration of measurements instruments or something is wrong from the measuring instrument
B) Random error
Unpredictable error caused either by weather or anything else.
Sources of errors
1. Experimentation error/modeling error
2. Truncation error/terminating error
E.g.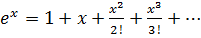 
You can see that the series is terminated at power of 3
3. Rounding off numbers
4. Mistakes and blunder
ABSOLUTE AND RELATIVE ERROR
Absolute error
Is the difference between the measured value of a quantity X0 and its value
Absolute error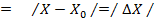
Relative error
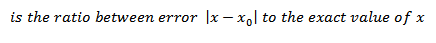
i.e. Relative error =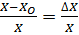 
A relative error gives an indication of how good measurement is relative to the size measurement is relative to the size of the thing that measured.
Example
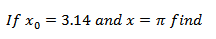
i) Absolute error
ii) Relative error
iii)Percentage error
Solution
i. Absolute error = /X – X0/
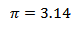
= X – X0
∆x = 0.001592654
ii. Relative error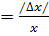 
= 
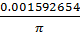
= 0.000050696(9dp)
iii. Percentage error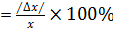 
= 0.000050696 x 100%
= 5.0696 x 10-2%
Roots by iterative methods
Iterative method is used to find a root of function by approximations repeatedly.
If f(x1), f(x2) < 0 the root lies between X1and X2
Newton’s Raphson formula
The formula is based on the tangent lines drawn to the curves through x-axis
Consider the graph below
Suppose f(x) = 0 has a root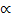 
that x is an approximation for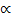 
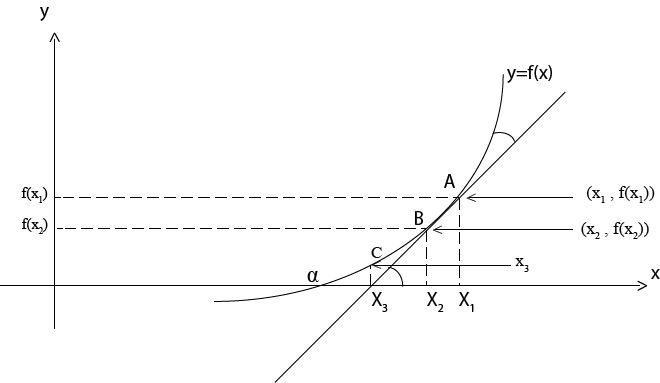
Choosing a point which is very close to  let be X1
X1→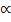
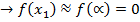
A line AB is drawn tangent to the curve at a point A where A(X1, f(X1))
X2 is the point which is very near to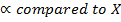 
1
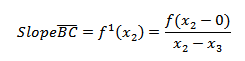
This slope is equal to the tangent of the curve at X=X1
i.e.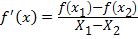 
But At B f(X2) = 0
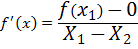
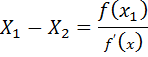
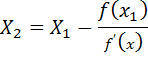
X3 will be the best approximation
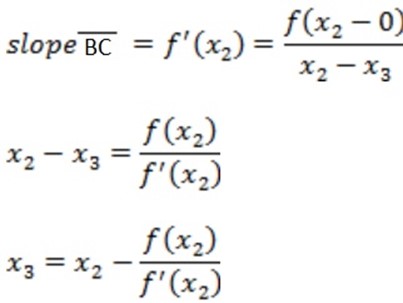
In general N-R formula can be written as
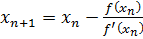
Example
Show that the equation X3 – X2 + 10x – 2 = 0 has a root between x = 0 and x = 1 and find the approximation for this root by carrying out 3 iterations
Solution
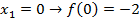
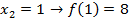
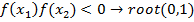
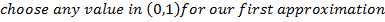
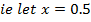
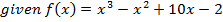
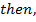
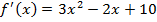
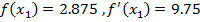
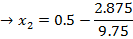
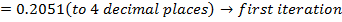
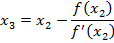
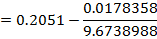
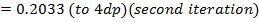
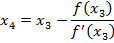
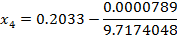
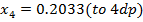
Application of N-R Formula
1. Find approximation for roots of numbers suppose we want to approximate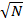 
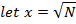
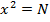
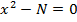
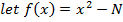
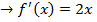
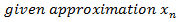
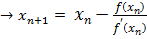
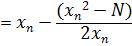
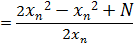
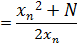
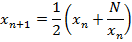
Example
B y using 2 iteration only and starting with an initial value 2, find the square root of 5 correct to four decimal place
Solution
Let x=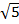
X2=5
X2 – 5 = 0
Let f(x) = x2 – 5 by N.R formula
f'(x)= 2x
Given X1=2
Then
First iteration
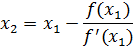
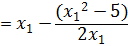
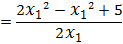
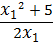
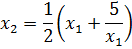
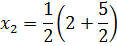
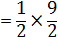
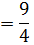
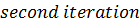
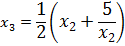
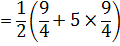
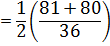
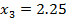
Example
Apply the N.R formula to establish the root of a number A
Solution
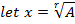
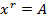
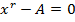
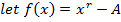
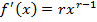
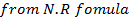
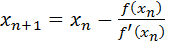
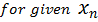
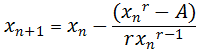
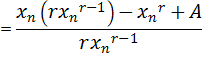
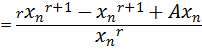
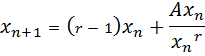
Finding approximations for reciprocals of numbers
Suppose we want to approximate 
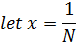
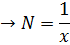
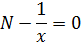
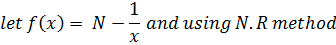
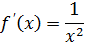
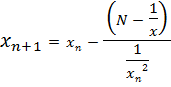
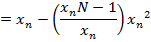
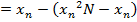
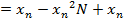
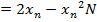
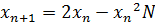
Example
Use N.R formula to find the inverse of 7 to 4, and perform 3 iteration only starting with Xo=0.1
Solution
