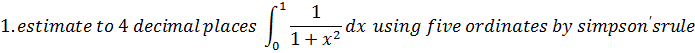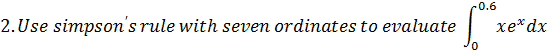SECANT METHOD
The secant method requires two initials values X0 and X1
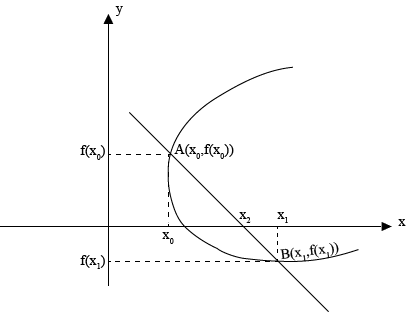
Line AB is a secant line on the curve f(x)
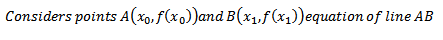
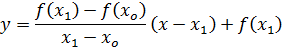
We find the roots of this, the value of x such as that y=0
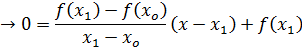
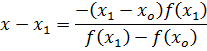
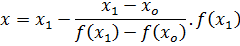
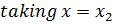
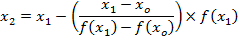
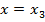
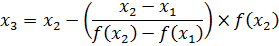
In general secant formula is given
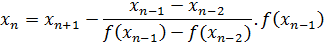
Comparison with Newton’s method
-Newton’s converges faster (order 2 against ≈1.6)
– Newton’s requires the evaluation of f and f1 at every step
-Secant method only requires the evaluation of f
Example
Calculate in 3 iteration the root of the function f(x)= x2-4x+2 which his between
X0=0 and X 1=1
Solution
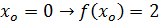

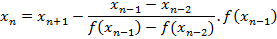
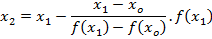
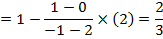
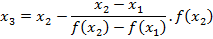

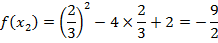

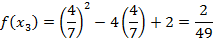
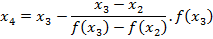

NUMERICAL INTEGRATION
Definite integral 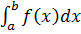 is used to determine the area between y= f(x), the x -axis and the ordinates x = a and x = b
is used to determine the area between y= f(x), the x -axis and the ordinates x = a and x = b
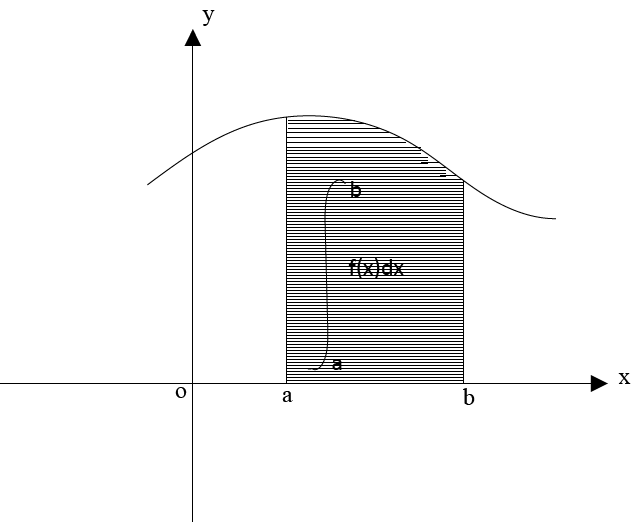
An approximate value for the integral can be found by estimating this area by another two methods
A. Trapezium rule
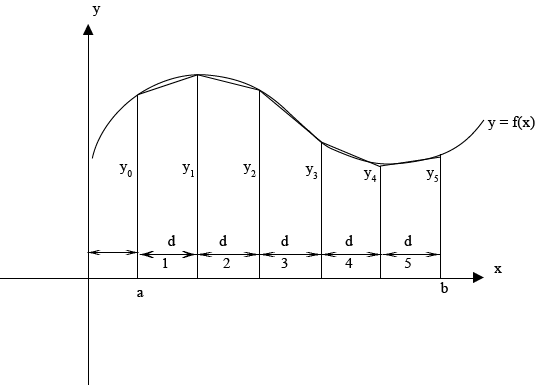


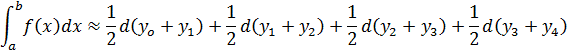
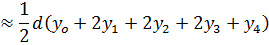
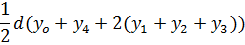
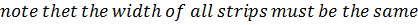
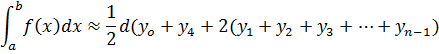
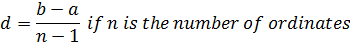
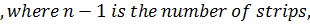
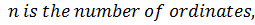
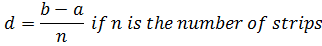
Example
Estimate to 4 decimal places 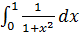
Using five ordinates by the trapezium rule
Solution
Taking five ordinates from X = 0 to X = 1
5 – 1 = 4 number of strips
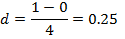
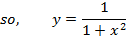
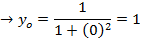
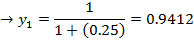
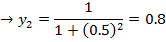
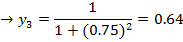
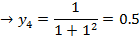
| X | 0 | 0.25 | 0.5 | 0.75 | 1 |
| Y | 1 | 0.9412 | 0.8 | 0.64 | 0.5 |
edu.uptymez.com
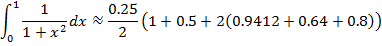
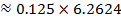
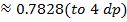
Simpson’s rule
Simpson’s rule is another method which can be used to find the area under the curve y= f(x) between x = a and x = b

A quadratic equation is fitted (parabola) passing through the three points i.e through A,B,C
Then

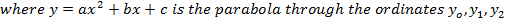

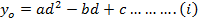
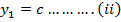
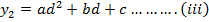
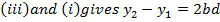
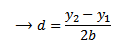


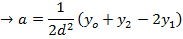
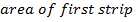
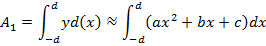
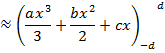
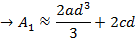
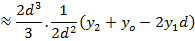


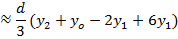
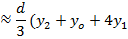
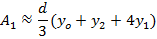
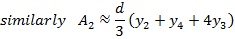
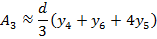
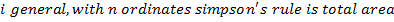
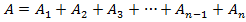
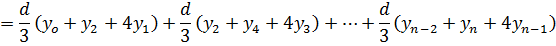
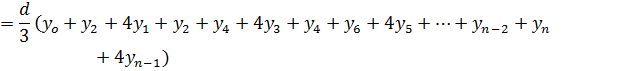
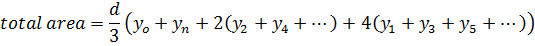
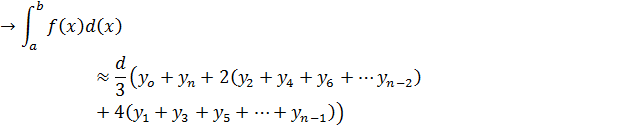
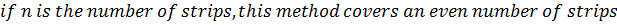
Example