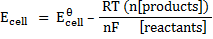Form 6 Chemistry – PHYSICAL CHEMISTRY 1.3- ELECTROCHEMISTRY

EFFECTS OF CONCENTRATION AND TEMPERATURE ON CELL POTENTIALS

We have been considering electrode potential under standard conditions of molar solution, pressure of 1 atom and 298K. When the conditions are altered he values of electrode potential changes thus we have to define the potential of the cell under non-standard conditions.

The Nernst equation shows the relationship between emf of the cell at standard conditions and emf under non-standard conditions.

Where; 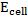 – emf of a cell at any conditions

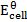 – emf of a cell under standard conditions

R – Universal gas constant (8.314 Jmol^-1K^-1)

n – Number of moles electrons being transferred

F – Faraday’s constant (96500c)

At standard temperature (298K)

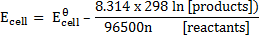
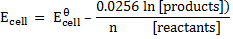
OR

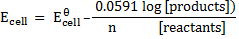
The above equation can be applied to half reactions and overall reactions

NOTE
Always write a balanced cell reaction to obtain ‘n’ and position of ions, either reactants or products together with their stoichiometry

Example

Calculate the emf of the given cell at standard temperature.

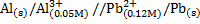
Given

Alternative Solution 1

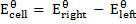
= -0.13 – (-2.56)

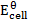= 2.43v

Alternative Solution 2

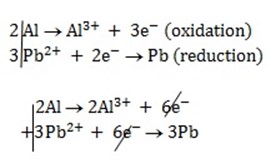
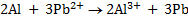
n = 6

Now;

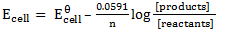
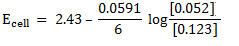
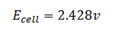
Example 2

Calculate the emf of Daniel cell at 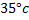 using 2M ZnSO4 solutions and 0.5M CuSO₄ solution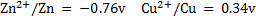   

Alternative Solution 1

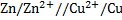
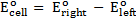
= 0.34 – (-0.76)

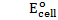 = 1.1v

Alternative Solution 2

Half reactions

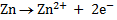(Oxidation)

 (Reduction)

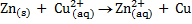
Here n = 2

Now using

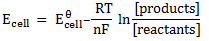
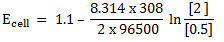
E_cell =1.08v

Example 3

Calculate the emf for the following voltaic cells

a)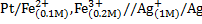     

(b)Zn/Zn²⁺(10^-3M)//Ag⁺(10^-3M)/Ag

c)     

Given

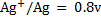
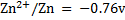
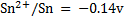
Alternative Solution 1

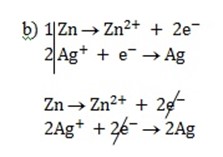
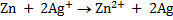
n = 2

Now;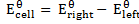

= 0.8 – (-0.76)

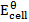= 1.56v

Alternative Solution 2

From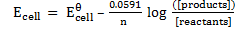

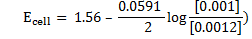
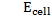= 1.47v

d)  Solution

Alternative Solution 1

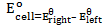
= 0.8 – (0.77)

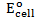= 0.03v

Alternative Solution 2

Half reactions

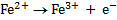
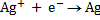
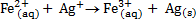
n = 1

From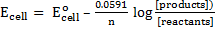

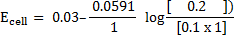
E_cell =0.0122v

c)  Solution

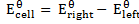
= -0.14 – (-2.56)

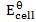= 2.42v

Half reactions

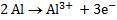
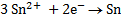
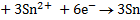
2Al + 3Sn²⁺ ® 2Al³⁺ + 3Sn

n = 6

Now;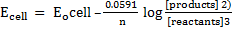

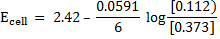
E_cell =2.418v

EQUILIBRIUM CONSTANT OF GALVANIC CELL
Consider to what happens to a Daniel’s cell if we use it to do some electrical work i.e. it can be connected to a small electric motor. After sometimes the motor will stop. The cell will run down. When this happens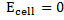 and there is no overall transfer of electricity from one half cells to the other. When there is no overall change taking place in a chemical reaction the equilibrium has been established. At equilibrium, electron density of both electrodes is equal and there is no transfer of electricity between the two half cells.

Applying the Nernst equation to a Daniel’s cell

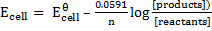
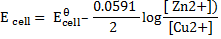
Since the reaction is at equilibrium, the ratio

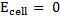
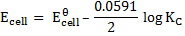
K_C = 1.67 x 10³⁷

The large value tells  us that, the equilibrium lies almost entirely in favour of copper metal and zinc ions.

Generally, the cell at equilibrium at standard temperature is given by the following expression;

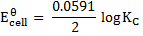
Example

Calculate K_C for the following voltaic cell

Given

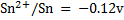
Cell reaction

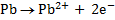
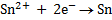
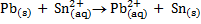
From

= -0.12 – (-0.46)

= 0.34v

Now,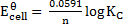

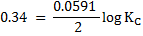
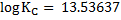
K_C = 3.20 x 10¹³

Example
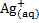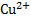What concentration of  will emf of the cell be zero at  if concentration of  is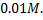

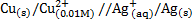
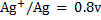
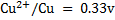
Solution

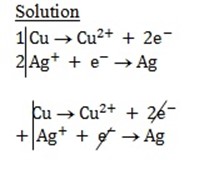
Cu + 2Ag⁺ ® Cu²⁺ + 2Ag

n = 2

From

When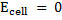

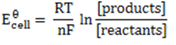
Now,

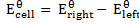
= 0.8 – (0.338)

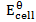  = 0.462v

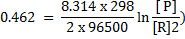
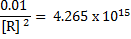
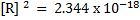
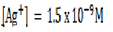
3. Given 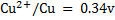 and 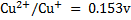   . Calculate the equilibrium constant for the reaction  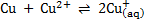 State the significance of equilibrium constant.

Solution

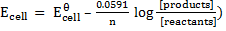
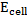 = 0

 

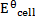
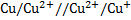
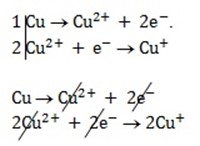
Cu + 2Cu²⁺ ® 2Cu⁺

n = 2

Using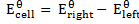

= 0.53 – 0.34

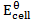 = -0.187v

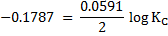
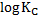 = -6.3282

K_C = 4.69 x 10^-7

Question
(a) Given the  which is thermodynamically feasible, the reduction of Cu²⁺ by Ag or reduction of Ag⁺ by Copper.

(b) Calculate the standard emf of the cell and the equilibrium constant.

CONCENTRATION CELL

A half concentration cell which consists of two half cells with identified electrode that differs in ion concentration because the electrodes are identified.   for oxidation is numerically equal and opposite in sign to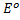 for reduction. As a result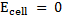

The reaction in the cell takes place in order to reduce the difference in concentration until (when the two concentrations are equal. The higher concentration is reduced and the lower concentration is increased.)

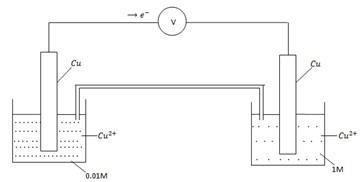
Oxidation                                                                 reduction

Cu ® Cu²⁺ + 2e^–                                                     Cu²⁺ + 2e^– ® Cu

Electrochemical cell: Anode (-)

Cathode (+)

Electrolytic cell: Anode (+)

Cathode (-)

Question

Calculate the emf of the following concentration cell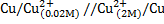

Solution

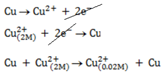
Using Nernst equation

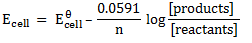
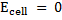
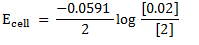
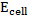= 0.0591v

3. MEASUREMENT OF pH OF A SOLUTION USING STANDARD ELECTRODE POTENTIAL

pH is the degree of alkalinity, or acidity of a substance. It is obtained by using the hydrogen ion concentration pH = –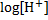

The pH of a solution is determined by using any electrode provided its standard electrode potential is known and the concentration of ions in that electrode should be 1M. This will be one of the half cells another half cell is made up hydrogen electrode dipped into the solution whose pH is to be determined

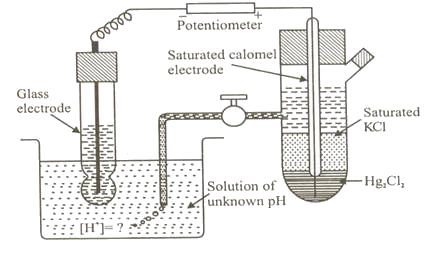
Reaction:

H_2(g) + 2 H⁺_(aq) +2e^–                       E ⁰ = 0.00v

2Ag⁺ _(aq)+ 2e^–
 Ag_(s)                   E = 0.8v

H_2(g) + 2Ag⁺_(aq) 2H⁺_(aq0+ Ag_(s)        E⁰   = 0.8V

Applying Nernst equation at standard temperature

E _cell = 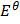 _cell –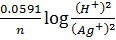  

= 0.8 –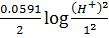

= 0.8 + 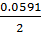2(-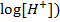

E _cell = 0.8 + 0.0591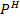

pH=   =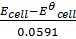

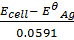
Question:    Calculate the 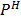 of the following cell and hydrogen ion concentration.

Zn/Zn²⁺ // H⁺ /H₂, pt

Zn²⁺ /Zn = -0.76v

E _cell = 0.115v

Solution

= 0 – (-0.760)

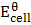 = 0.76v

 =  –

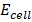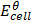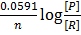
Zn_(s)   →  Z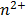_(aq)  +  2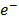

2H⁺_(aq)  +  2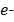  → 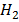 _(g)

Zn_(s) + 2H⁺_(aq)  Zn²⁺_(aq)+ 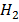_(g)

 =  –  

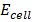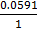
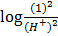
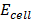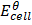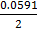 =  +  x 2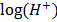

0.115 = 0.76 + 0.0591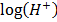

-0.0591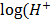) = 0.645

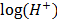– = 10.913

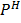 = 10.91

            pH DEPENDENCE OF REDOX POTENTIALS

Whenever a redox half equation involves H⁺ or OH ion, its redox potential depends on the 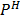 of the solution.

Example

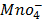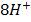 _(aq)+  _(aq)+ 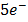  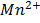 _(aq)+ 4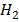O_(l)      E = 1.52V

The Nernst equation at standard temperature is

 =  –

 =  –

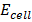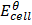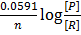
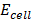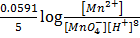
Under standard conditions, all effective concentrations are 1M

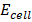 = 1.52 –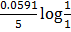

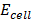 = 1.52 – 0

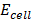 = 1.52v

Suppose the 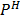 is changed from O to 5 i.e. the concentration changes from 1M to  1 x 10^-5 M

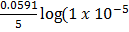 = 1.52 – )^-8

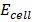 = 1.52 +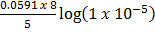

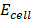 = 1.04 v

Due to change of 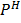 from O to 5, the electrode potential decreases from 1.52 to 1.047v.
That means, permanganate (vii) becomes a less powerful oxidizing agent when PH increases

Question1.
Calculate 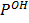 of the following cell;-

Zn/Zn²⁺ //H⁺ /H₂, pt

Zn²⁺ /Zn = -0.76v

E _cell = 0.115v

Question2.
If E for Zn /Zn²⁺//Cn²⁺/Cn is 1.1v

i.Calculate the E _cell when concentration of Zn²⁺ is 2M and Cu²⁺ is 0.5M

ii.What is E _cell when concentration of Zn is 0.4M,  = 0.1M

Question3.
Write down the expression for the cell emf for the following reaction;

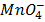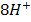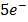
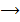
 _(aq)+  _(aq)+   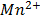 _(aq)+ 4H₂O_(l)

Briefly explain why the oxidizing power of permanganate (Vii) ion is quite sensitive to the concentration of H⁺ in the solution.