Form 6 Chemistry – PHYSICAL CHEMISTRY 1.4-CHEMICAL EQUILIBRIUM

UNITS OF EQUILIBRIUM CONSTANT

The units of equilibrium constants, K _c and K _p depends on the number of moles of reactants and products involved in the reaction

1. N_{2 (g)}   + O_{2 (g)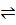}      2NO _(g)

     K _p =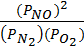      

     K _p = 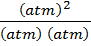  = Unit less

2. N_{2 (g)} + 3H_2(g)      2NH_{3 (g)}

       K _p =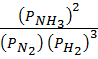  

       K _p =       

       K _p =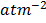

       K _{c =}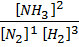

           =

      K _c =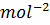

A large value of K _p or K _c means the equilibrium lies on the sides of the product and a small value of K _c and K _p means equilibrium lies on the sides of the reactants thus the equilibrium constant shows to what extent the reactant are converted to the product.

        If K _c is greater than 10³, products pre- dominate over reactants equilibrium therefore the reaction proceeds nearly to completion.

        If K _c is less than 10^-3, reactants dominate over products, the reaction proceeds to very small extent.

        If K _c is in the range of 10^-3 and 10³, appreciable concentrations of both reactants and products are present.

SOLIDS AND PURE LIQUIDS IN EQUILIBRIUM EXPRESSION

The concentration of a solid or pure liquid (but not a solution) is proportional to its density. Therefore, their densities are not affected by any gas pressure hence remain constant; hence their concentration never appear in the equilibrium expression.

Example

1. What is the equilibrium expression for the following reactions?

     i)   3Fe _(g)   + 4H₂O _(g) 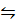   Fe₃O₄ + 4H_{2 (g)}

      Solution

       K _c =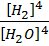          _OR     K _p =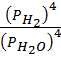  

      ii)  PCl_5
(g) 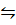   PCl_{3 (g)} + Cl _2
(g)

            K _c =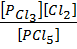 

           K _p =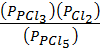

     iii)  HCl _(g) + Li H_(S) 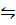   H_{2 (g)}   +LiCl_(s)

         K _c =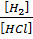  

         K _p =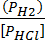

     iv)  Cu (OH) _2(s)   Cu²⁺ _(aq) + 2OH ^–_(aq)

                 K _c = [Cu ²⁺]   [OH ^–] ²

     v)   CaCO_3(s) 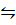 CaO_(s) + CO _2(g)

                    K _c = [CO₂]

     vi)    [Cu(NH₃)₄]²⁺_(aq)      Cu²⁺_(aq) + 4NH_3(aq)

                    

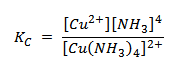
2. The equilibrium constant for the synthesis of HCl, HBr and HI are given below;

          H_{2 (g)} +Cl_{2 (g)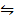}     2HCl _(g) K_C =10¹⁷

          H_{2 (g)} + Br_{2 (g)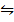}       2HBr _(g)   K_C=10⁹

          H_{2 (g)} +I _2(g) 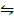      2HI _(g)    K_C=10

3.   a) What do the value of K_c tell you about the extent of each reaction?

      b) Which of these reactions would you regard as complete conversion? Why?

Answers

a) For all the 3 reactions, the equilibrium lies on the product side (i.e. RHS) and the extent of formation of HCl is greater than HBr which in turn is greater than HI.

b) For the 1^st and 2^nd reaction, it can be regarded as complete conversion because products pre-dominates over reactants at equilibrium.

Characteristics of equilibrium constant

1. Equilibrium constant is applicable only when the concentrations of reactants and products have attained their equilibrium.

2. The value of equilibrium concentration is independent of the original concentration of reactants.

3. The equilibrium constant has a definite value for every reaction at a particular temperature.

4. For a reversible reaction the equilibrium constant for the forwarded reaction is the inverse of the equilibrium constant for the backward reaction.

5. The value of equilibrium constant tells the extent to which reaction proceeds in the forward or reverse direction.

6. Equilibrium constant is independent of the presence of catalyst. This is because the catalyst affects the rate of forward and backward reaction equally.

Relationship between K _c and K _p for a gaseous equilibrium

For any given reaction, K_c or K_p is a function of the reaction itself and temperature.

Consider the following gaseous equilibrium

    aA _(g) + bB_(g) 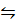    cC _(g) + dD _(g)

       K _c = 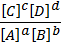    —————— (1)

       K _p = 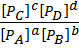 ————– (2)

From PV= nRT

          [X] =  =

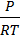
I.e. [A] = 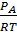    , [B] =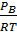

Substitute these concentration in terms of partial pressures in equation (1)

            K _c =

      =  .

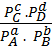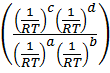
           = K _p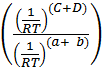

             = K _p

But;   (c+d) = total number of moles in the products.

         (a +b) = total number of moles in the reactants.

         (c +d) – (a + b) = The difference between moles of products and reactants

So,    (c +d)-(a + b) = Δn

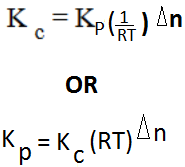
Thus, the numerical value of K _p and K _c are equal when there is the same number of moles on products and reactants side numerically.
Example:

1. What is the relationship between K _p and K _c in the following reactions?

   2H_{2 (g)} + O_{2 (g)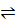}   2H₂ O _(g)

From; K _p = K _c (RT) ^Δn

         = K _c (RT) ^{(2- (1+2))}

        K _p = K_c (RT)^-1

ii) Derive the relationship between K _p and k _c for the particular reaction.

         2H_{2 (g) +} O_{2 (g)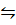}     2H ₂O _(g)

        K _c = 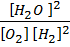  …………… (1)

        K _p = 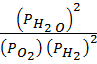  ……….. (2)

From  PV = nRT

             P = RT

             P = [X] RT

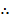
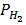   = [H ₂] RT ,  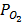 = [ 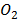] RT………etc

Substitute the partial pressure in equation (2)

        

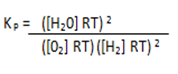
         K _p = .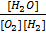

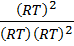
          K _p = K _c (RT) ^(2-(1+2))

                 K _p = K _c (RT)^-1

2. a) Derive the relationship between K _p and K _c for ammonic synthesis.

        N_{2 (g)} + 3H_{2 (g)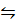}  2NH_{3 (g)}

         K _c =  ………… (1)

          K _P = 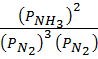 …….. (2)

From PV = nRT

           P = RT

           P = [X] RT

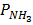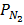  = [] RT, 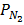= [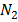] RT,   = [] RT

Substitute the partial pressure in equation (2)

       K _p =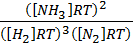

       K _P =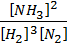 

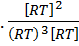
        K _p = K_C x

         K _p = K _C.(RT)^-2

b) If K_c = 0.105 mol^-2dm⁶ at 472⁰C. Calculate K _p

          [R=8.31 dm³ KPa mol^-1 K^-1]

Solution:

K _p = K _c x (RT)^-2

     = 0.105 x (8.31x 745)^-2

     = 0.105 x (6190.95)^-2

     = 2.7395x 10^-9(KPa)^-2

DETERMINATION OF EQUILIBRIUM CONSTANT

        Consider the reaction:-

           CH₃CH₂OH + CH₃COOH 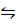  CH ₃COOCH₂ CH_{3 +} H₂O

                                                 

Example:

1. An equilibrium system for the reaction between H₂  and I₂, to form HI at 670K in 5l flask contains 0.4 moles of H₂, 0.4 moles of  I₂ and 2.4 moles of HI. Calculate the equilibrium constant K _c.

    H_{2 (g)} +I_{2 (g)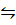}   2HI _(g)

       K _c =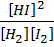 

     [HI] = 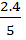  = 0.48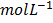

      [H₂] = 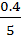= 0.08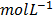

       [I₂] =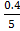  = 0.08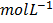

    K _c =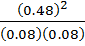  

           K _c = 36

2. A mixture of 1.0 x10^-3 moldm^-3 H ₂ and 2.0 x 10^-3 moldm^-3 I₂ are placed into a container at 450⁰C. After equilibrium was reached the HI concentration was found to be 1.87 x 10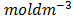^. Calculate the equilibrium constant.

                      H_{2 (g)} + I_{2 (g)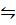}    2HI _(g)

At   t=0              a        b                   0

Equilibrium:  a-x       b-x               2x 

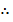2x = 1.87 x 10^-3

      X= 9.35 x 10^-4moldm ^-3

           a=1.0 x 10^-3

     a-x = 1.0 x 10^-3 – 9.35x 10^-4

            = 6.5 x 10^-5moldm^-3

       b = 2.0 x 10^-3

     b -x=2.0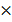10^-3– 9.35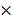10^-4

     =1.06510^-3moldm^-3

          K _c =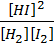

      =

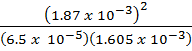
               K _c = 50.51

3. a) It was found that if 1 mole of acetic acid and half a mole of ethanol react to equilibrium at certain temperature, 0.422 moles of ethyl acetate are produced. Show that the equilibrium constant for this reaction is about 4.

                  

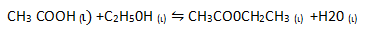
Start: –                  1mol               0.5mol                     0                                  0

Equilibrium:       1-0.422          0.5-0.422               0.422                                        x

                              0.578               0.078                   0.422                         0.422

Equilibrium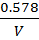                                                                   

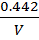
Concentration   

             K _c =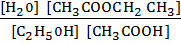  

             =           

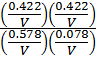
                  K _c = 3.95

              K _c ≈ 4   shown

b) From the same reaction above, 3moles of acetic acid and 5 moles of ethanol reacted. Find the amounts which will be present equilibrium.

                             CH₃COOH _(l) + C₂H₅OH _(l) 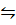        CH₃COOCH₂CH_{3 (I)} + H₂O _(I)

t= 0                              3                        5                                        0                                0

t = t                            (3-x)             (5-x)                                       x                              x

Equilibrium

Concentration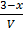                                                                                                  

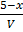
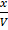
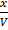
        K _c =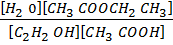   

        4 = 

       4 =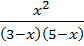

       4 =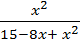          

       X²   = 60 – 32x + 4x²

         3x² – 32x + 60 = 0

      X = 8.24   or   x = 2.43

Logically;   x = 2.43

At equilibrium CH₃COOH 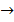     3 – 2.43 = 0.57 moles

                           C₂ H₅ OH 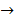      5 – 2.43 = 2.57 moles

4 .For the reaction;

CO_{2 (g)} + H_{2 (g)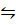}      CO _(g) +   H₂ O _(g)

The value of K _c at 552⁰C is 0.137. If 5moles of CO ₂, 5moles of H_2, 1 mole of CO and 1 mole of H₂ O are initially present, what is the actual concentration of CO₂, H_2, CO and H₂O at equilibrium?

                           CO_{2 (g)}      +    H_{2 (g)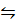}       CO_{2 (g)} +   H₂ O _(g)

At start;                      5                     1                       1               1

At equilibrium       5-x                   1-x                   1x              1x

       K _c   =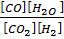

    0.137 =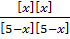

    0.137 =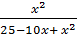

   3.425 – 1.37x + 0.137x²   = X²

  3.425 – 1.37x + 0.137 x²–x² =0

  3.425 -1.37x – 0.863x² =0

  x =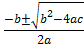

 x =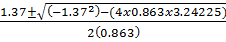    

   x =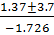   =     x =1.349

COMBINING EQUILIBRIUM REACTIONS

1. Reversing an equilibrium reaction

Consider the reaction

PCl_{5 (g)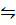}  PCl_{3 (g)} +Cl_{2 (g)}………………. (i)

K _{c (i)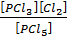} = _{…………………….. (i)}

Reversing the reaction;

         PCl_{3 (g)} + Cl_{2 (g)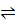}      PCl_{5 (g)}

K _{c (ii)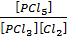} =   ………………. (2)

When reaction equation is reversed, the equilibrium constant is reciprocated i.e. from equation (1)   and (2)

     K _c(ii) =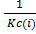

2.      Multiplying an equilibrium reaction by a number

When the stoichiometric coefficient of a balanced equation is multiplied by the same factor, the equilibrium constant for the new equation is old equilibrium constant raised to the power of the multiplied factor.

PCl_{5 (g)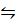}        PCl_{3 (g)} + Cl _(g)

K _{c (i)} =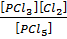 

If the equation (i) is multiplied by ½

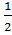PCl_{5 (g)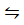}   PCl_{3 (g)} + Cl_{2 (g)}

        

 

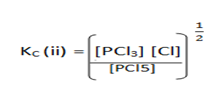
Note; if an equilibrium reaction is multiplied by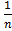     then;

   K _{c(ii )} =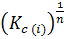        

   K _c(ii)   =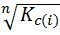

Example: The K _c for the reaction below is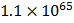

S _(s) +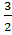 O_{2 (g)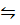}   SO_{3 (g);} what is the K _c for SO₃ Equilibriate with S + O₂

2 SO_{3 (g)}     2S_(s) + 30_2(g)

S _(s) +  O_{2 (g)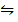}   SO_{3 (g})………………. (I)

2SO_{3 (g)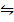}         2S_(s) + 30_2(g)…………………. (2)

Equation (2) has been reversed and multiplied by 2

When reversed

K _{c (i)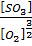} =       = 1.1×10⁶⁵

   K _{c (ii)} =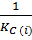    

K _{c (ii)} =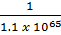     

K _{c (ii)} = 9.09 x 10^-66

When multiplied

K _{c (ii)} =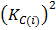

3. Adding the equilibrium. 

The equilibrium constant for the reaction

i) 2HCl_(g) 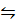   Cl_2(g) +H_2(g)

   K _{c (i)} = 4.17x 10^-34   (At 25 ⁰ c)

The equilibrium constant for reaction

ii)  I_{2 (g) +} Cl_{2 (g)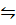}     2ICl _(g)

       K _{c (ii)} = 2.1 x 10⁵ (At 25 ⁰c)

Calculate the equilibrium constant for the reaction

iii) 2HCl _(g) + I_{2 (g)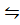}      2ICl _(g) + H_{2 (g)}

K _{c (iii)} =?

K _{c (i)} =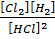

K _{c (ii}) =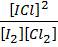  

K _{c (iii)} =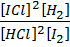  

When equation (i) + equation (ii) = equation (iii), Hence

K _{c (iii)} = K _{c (ii)} x K _{c (i)}

           = (2.1 x 10⁵) x (4.17 x 10^-34)

K _{c (iii)} = 8.757 x 10^-29
(mol dm^-3)^1/2

Question 1:

The following are reactions which occurs at 3500K

i) 2H_{2 (g)} +O_{2 (g)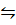}    2H₂O _(g)    K _{p (i)} = 26.4 atm^-1

ii) 2CO _(g) +O_{2 (g)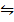}   2CO_{2 (g)} K _{p (ii)} = 0.376 atm^-1

Calculate  equilibrium constant for reaction

CO _{2 (g)} + H _{2 (g)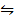}       CO _(g) + H₂O _(g)

K _{p (iii)} =?

Question 2

.Determine the Equilibrium constant for reaction;

  M_2(g) +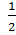O_{2 (g)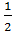} +Br_{2 (g)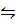}  NOBr _(g)

Given that:-

i/ 2NO _(g) 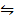  N_2(g) + O_2(g)   K _c = 2.4 x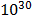

ii/ NO _(g) +  Br_2
(g) 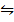 NOBr     K _c = 1.4

Answers

i) 2H_{2 (g)} + O_2
(g) 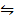    2H₂ O _(g)                                                                K _{p (i)} =26.4atm^-1

ii) 2CO _(g) + O_{2 (g)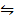}      2CO_2
(g)                                                                K _{p (ii)} =0.376 atm^-1

iii) CO_{2 (g)} + H_{2 (g)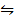}         CO _(g)   + H₂O _(g)                                        K _{p (iii)} =?

K _{p (i)} = 

K _{p (ii)} =

K _{p (iii)} =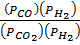  

Reverse (ii), multiply (i) and (ii) by ½

i)  (2H_{2 (g)} +O_{2 (g)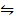}      H₂O _(g))                                    K _{p (i)} =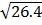  

i) H_{2 (g)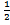} + O ₂ 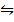           H₂O _(g)                          K _p(i) = 5.138 atm^-1

Reverse (ii)

ii) 2CO_{2 (g)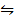}   2CO _(g) +O_{2 (g)}                                     K _{p (ii)} =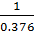    

                                                                                      = 2.6595 atm^-1

Now multiply by (ii) by ½

 (2CO_{2 (g)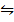}    2CO _(g) +0_2(g))                                K _{p (ii)} =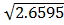       

ii) CO_{2 (g)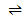}  CO _(g) +    O_{2 (g)}                                             =1.63079

Add equation (i) + (ii), then

K _{p (iii)} = K _{p (i)} x K _{p (ii)}

              = 5.138 x 1.63079

              =8.379 atm^-1

2. i) 2NO_(g) 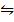         N_2(g)     +  O_2(g)                                                             K _c(i) = 2.4 x 10³⁰

   ii) NO _(g) + 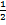Br _(g)  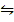         NOBr _(g)                                                           K _{c (ii)} =14

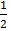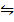   iii)  N_{2 (g)} +   O_{2 (g) +}   Br _(g)        NOBr_(g)                           K _{c (iii)} =?

Reverse ……. (i)

O_{2 (g)}   + N_{2 (g)}    2NO _(g)                                                                       K _{c (i)} =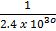          

                                                                                                                 =4.167 x 10^-31

Now multiply (i) by ½

  O_{2 (g)}   + N_{2 (g)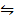}   NO _(g)                                                                   K _{c (i)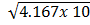} =^-31

                                                                                                                 =6.455 x 10^-16

Equation (i) + (ii) = (iii)                                                       

Therefore:

K _{c (iii)} = K
_{c (i)} x K _{c (ii)}                                                    

              = 6.455 x 10^-16 x 1.4

              = 9.0369 x 10^-16(mol dm^-3)^1/2 

3. The equilibrium constants for the reactions which have been determined at 878K are as follows:-

i) COO _(s) + H_{2 (g)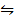}     CO_(s) + H₂O _(g)              K₁ = 67

ii) COO_(s) + CO _(g) 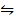        CO_(s) + CO_{2 (g)}                        K₂ = 490

Using these information, calculate K’s (at the same temperature) for;

iii) CO_{2 (g)} +H_{2 (g)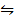}   CO_{2 (g)} + H₂O _(g)            K₃ =?

And commercially important water gas reaction

iv) CO _(g) + H₂O_(g) 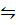    CO_2(g)+ H_2(g)                                        K_4=?

Reverse (ii)

(ii)CO_{2 (g)} + CO_(s)    CO _{(g) +} COO _(g)          K₂=2.0408 x 10^-3

Equation (i) + (ii) = (iii)

 K₃ = K ₁ x K₂

          = 67 x 2.0408 x 10^-3

          K₃ = 0.1367

To find K₄

i) COO _(s) +H ₂        CO _(s) + H₂O _(g)                          K₁= 67

ii) COO_(s) + CO _(g)        CO _(s) + CO_{2 (g)}                         K₂ = 490

iii) CO_{2 (g)} + H_{2 (g)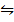}            CO _(g) + H₂O _(g)                                  K₃ = 0.1367

iv) CO _(g) + H₂O _(g) 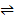      CO_{2 (g)} + H_{2 (g)}                                       K₄ =?

When equation (iii) is reversed, it is equal to equation (iv)

 K₄ =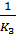   

         =

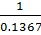
         = 7.315

4. The heterogeneous equilibrium

    i) Fe_(s) + H₂O 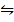       FeO_(s) + H_{2 (g)}                     

    ii) Fe_(s) + CO_{2 (g)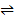}     FeO_(s) + CO _(g)

Have been studied at 800 ⁰c and 1000 ⁰c.Also the rate (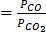) is constant = 1.81 at 800⁰c and 2.48 at 1000 ⁰c.

    i) Why are the ratios constant?

    ii) Calculate equilibrium constant at two temperatures of the reaction

    iii)  H₂O _(g)    + CO _(g) 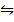             H_{2 (g)    +}     CO_{2 (g)}      

Answer:

i) The ratios are constant because for any system in equilibrium at a given temperature, the ratio of products of concentration of products to the product of concentration of reactants raised to the point of their mole ratios is constant.

ii) At 800 ⁰C

K _p1 =2

K _p2 =1.81

K _p3 =?

(i)       Fe_(s) + H₂O_(l)    Fe_(s) + H_{2 (g)}                                                 K _{p (i)} =2

Reversed (ii) CO _(g) + FeO_(s) 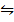                Fe_(s) + CO_{2 (g)}              K _{p (ii)} =?

Equation (i) + (ii) = (iii)    

            K_p1 x Kp₂=K_p3

            K_p3 = K_p1 x K_p2

                  =2 x 0.55

             K_p3 = 1.1

At 1000 ⁰c

K_p1 = 1.49

K _p2 =2.48

            i) Fe_(s) + H₂O _(g) 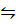          FeO_(s)   +   H_{2 (g)}                     K _p1 =1.49

Reversed     ii)     CO _(g) +   FeO_(s) 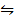        CO_{2 (g)} + Fe_(s)                  K_p2 =   

                                                                                                   =0.403

Equation (i) + (ii) = (iii)

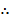           K_p3 =k_p1 x k_p2

                     = 1.49 x 0.403

              K_p3 = 0.6

 1: When 1 mole of ethanoic acid is maintained at 25 ⁰c with 1 mole of ethanol, 1/3 of ethanoic acid remain when equilibrium is attained. How much would have remained if  3/4 of 1 mole of ethanol had been used instead of 1mole at the same temperature.

                      CH₃CH₂OH + CH₃COOH 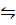   CH₃COOCH₂CH₃ + H₂O

At start:                1mol              1mol                            0                            0

At time:                 1-x                 1-x                              x                           x

At equilibrium:     11- x =                                                      

                                           

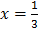
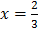
    K _c =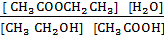     

           =              

             =                   

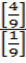
             K_c = 4

                           CH₃CH₂OH + CH₃COOH              CH₃COOCH₂CH₃ +H₂O

At start;                   1mol                   1mol                          0                           0  

At time                     1-x                       1-x                           x                          x

At equilibrium      (1 x 3/4)-x               1-x                           x                            x

K_c =                                        

4 =    =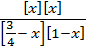

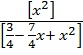
       4 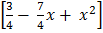=X²

         3- 7x + 4x² = x²

      3- 7X + 4X² – x² =0

        3x² + 3 – 7x = 0

        3x² -7x + 3 = 0

         a       b     c

          x =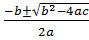

           x =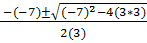

            =

        =   

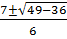
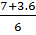
   X= 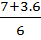           or    x =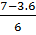

     = 1.76                    =    0.566

  X cannot be 1.76

           X = 0.566

– 0.566 = 0.184 moles or 23/125 moles

0.184 moles of ethanol would have remained

 2. The equilibrium constant (K _c) for the reaction; 2HI _(g) 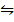     H_{2 (g)}   +I_{2 (g)} is 0.02 of 400 ⁰ c. If 2 moles of H₂ and 1 mole of I₂ were mixed together in a 1.0dm³ at 400 ⁰c, how many moles of HI, I₂ and H₂ would be present at equilibrium.

2HI _(g) 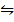        H_{2 (g)}    +   I_{2 (g)}                          K _c = 0.02

Reverse the equation above

                          H_{2 (g)}    +   I_{2 (g)}                2HI _(g)                     K_c =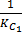  

At start                   2            1                           0                         

At time                 2-x         1-x                  2x  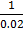                        =    = 50    

At equilibrium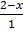                                 

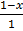
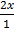
                K _c =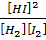   

                50 =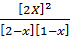   

                50 =   

          50 (2 – 3x + x²) = 4x²

         100 – 150x + 50x² = 4x²

        100 – 150x +5 0x² – 4x² = 0

         100 – 150x + 46x² = 0

       x=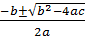

          =

         =

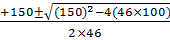
        x= 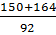                  or      x=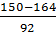  

        x= 2.33                                  x = 0.934

        x cannot be 2.33

               x = 0.934

At equilibrium:

Number of moles of H₂ = 2- 0.934

                                         =1.066moles

Number of moles of I₂= 1-0.934

                                        =0.066 moles

Number of moles of HI = 2 x 0.934

                                        =1.868 moles

3. The equilibrium constant for the reaction; H_{2 (g)} +Br_{2 (g)}             2HBr _(g) at 1024K is 1.6 x 10⁵. Find the equilibrium pressure of all gases if 10 atm of HBr is introduced into a second container at 1024K.

           H_{2 +} Br₂       2HBr