Form 6 Chemistry – PHYSICAL CHEMISTRY 1.5-SOLUBILITY

What is solubility ?
Is amount of substances dissolves in water completely so as give free ions.
Since the amount can be in gram (g)  or in moles (mol) then the S .I unit for solubility is g/L or g/dm₃
Also solubility can be expressed in mol / dm³ or mol/L .  When solubility of substances is expressed in mol / dm³ and that is called molar solubility.

What is  molar solubility ?
It is amount of solute in moles dissolve in a given dm³ of of solvent to give free ions.
When solubility is expressed in it’s S.I unit  , that is the same as concentration in g /L or g /dm³  and when it is expressed as molar solubility , that is the same as molarity.
example. a) Define the following :
i) Solubility
ii) Molarity solubility
b) Calculate the following solubility in g /L 0.0004 M Na0H :-
i) Solubility is defined as the amount of a substance dissolve in water completely to give free ions.
ii) Molar solubility is  the amount of solute dissolves in moles in a given  dm³ of to give free ions.

Solution :-
i)Na0H Solubility = solubility in mol / dm³ x Mr
= 0.0004 x 40
= 0.016 g/L
The solubility of Na0H is 0.016 g /L

Solution:
ii) 2.7 x 10^-3 mol /dm³ Ca(0H)₂

Solubility  = molar  x Mr .
= 2.7 x 10 ^-3 x 74
= 0.1998 g/ L
The Solubility of Ca(0H)2 is  0.998 g/ L .

iii) 3.24 g of sodium chloride .
Solution:
Solubility  = Molar Solubility x Mr
= 3.24 g/L x  58.5
58.5
= 3.24 g/L
These solubility of sodium chloride = 3.24 g/L

SOLUBILITY PRODUCT OF SPARINGLY SOLUBLE SALTS
Many salts which are referred to as insoluble do infact dissolve to a small/limited extent. They are called sparingly or slightly soluble salts.

In a saturated solution, equilibrium exists between the ions and undissolved salt.

              
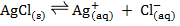
NOTE;
There is a limited number of ions that can exist together in water and this cannot be increased by adding more salts.

In a saturated solution of AgCl in contact with the ions, the equilibrium law can be applied

                      

                           

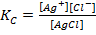
 The concentration of solid is taken as constant at constant temperature

         

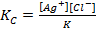
         Kc + K = [Ag⁺][Cl^–]

          Ksp = [Ag⁺][Cl^–]

          Ksp = Solubility product constant.

By definition, Ksp is the product of maximum concentration of ions of sparingly soluble salt that can exist together in a solution at a given temperature.

OR
It is the product of concentration of all the ions in a saturated solution of sparingly soluble salts.
OR
Solubility product is the product of ions concentration in mol/dm³ of a certain solution raised to their stochiometric coefficient

Solubility product is denoted by Ksp

The unit for Ksp depends on the stochiometric coefficients of the respective ions of such particular substance

How to write Ksp expressions

In writing Ksp expressions one should look on

Ionization equation should be written correctly and balanced.
Stochiometric coefficients become powers of the respective ion.

 Generally, for sparingly soluble salts

          AxBy 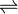 xA^y+ + yB^x-

           Ksp = [A^y+]^x[B^x-]^y

E.g. Write Ksp expression for the following equilibrium

(i)     Al(OH)₃    Al³⁺+ 3OH^–

 (ii)   Ag₂CrO₄  2Ag⁺ CrO₄^2-

Solutions:

(i)Ksp = [Al³⁺] [OH^–]³

(ii)Ksp = [Ag⁺]² [CrO₄
^2-]

(iii)(Ca₃(PO₄)₂     3Ca²⁺  +  2PO₄^3-

Ksp = [Ca²⁺ ]³  [PO₄
^3-]²

Significance of Ksp
(i) Ksp value is used in the prediction of occurrence of precipitates if ions in the solution are mixed.

If concentrations of ions are enough to reach Ksp value, salt precipitation occurs

Determination of Solubility product from solubility measurements

The Ksp value of the salt can be determined from its solubility in moles per litre (mol/L)

When concentrations are given in any other units such as g/L, they must be converted to mol/L

 Example 1
The solubility of AgI is 1.22 x 10^-8 mol/L. Calculate the Ksp for AgI

Solution

AgI_(s) 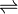       Ag⁺_(aq) + I^–_(aq)
Each 1 mole of AgI that dissolves gives 1 mole of Ag⁺ and 1 mole of I^– in solution, concentration of each ion solution is 1.22 x 10^-8 mol/L.

Hence

            AgI_(s) 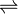     Ag⁺     +        Cl^–

                            1.22 x 10^-8          1.22 x 10^-8

                  Ksp = [Ag⁺] [Cl^–]

                         = (1.22 x 10^-8)²

            Ksp = 1.4884 x 10^-16 mol²L^-2

 Example 2
PbCl₂ dissolves to a slightly extent in water according to the equation

PbCl_2(s)
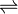   Pb²⁺_(aq)  + 2Cl^–_(aq)

Calculate the Ksp for PbCl₂ if (Pb²⁺) has been found to be 1.62 x 10 ^-2 mol l^-1.

Solution

PbCl₂          Pb²⁺                    +              2Cl^–

1.62 x 10 ^-2      1.62 x 10 ^-2          (2x 1.62 x 10^-2 ) 

      Ksp = [Pb²⁺] [Cl^–] ²

             = 1.62 x 10 ^-2 molL^-1 x 1.0497 × 10^-3 mol²L^-2
Ksp = 1.7005 x 10 ^-5 mol³L^{-3  .}

 Example 3
The solubility of Pb(CrO₄)is 4.3 x 10 ^-5 gl^-1. Calculate the Ksp of Pb(CrO₄)

(Pb =207, Cr = 52, O = 16)

Solution

PbCrO₄ 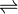       Pb²⁺     +     CrO₄
^2-

4.3 x 10 ^-5gl^-1     4.3 x 10 ^-5 gl^-1    4.3 x 10 ^-5gl^-1

To calculate the molar mass of (PbCrO4)

Pb(207) +Cr(52) +O(16)4=323gmol^-1

323g     → 1mole

4.3×10^-5 → x

x=1.33×10^-7mol

PbCrO₄        Pb²⁺     +     CrO₄
^2-

1.33 x 10 ^-7   1.33 x 10 ^-7   1.33 x 10 ^-7

 Ksp = [Pb²⁺] [CrO₄
^2-]

         = (1.33 x 10^-7)²

           Ksp = 1.76 x 10 ^-14 M²

 Example 4
100 ml sample is removed from water solution saturated with MgF₂ at 18^oC. The water is completely evaporated from the sample and 7.6mg of MgF₂ is obtained. What is the Ksp value for MgF₂ at 18^oC

Solution

V =100 ml
m= 0.076g.

       62g     →       1 mole

        0.076g  →       x

         x = 1.22 x 10 ^-3 molel^-1

MgF₂         Mg²⁺         +          2F^–

1.22 x 10 ^-3    1.22 x 10 ^-3         (2 ×1.22 x 10 ^-3 )

Ksp = [Mg²⁺] [F^–] ²

         = (1.22 x 10 ^-3) (2.44 x 10^-3)

    Ksp = 7.33 x 10 ^-9 moll^-1