Form 6 Chemistry – PHYSICAL CHEMISTRY 1.5-SOLUBILITY

DETERMINATION OF MOLAR SOLUBILITY FROM Ksp VALUE

If the Ksp value is known, the molar solubility can be obtained since Ksp shows the maximum concentration of ions which exists together in a solution.

Example 1

Calculate the molar solubility of Ag₂CrO₄ in water at 25^oC if its Ksp is 2.4 x 10^-12 M³.

      Ag₂CrO_4(s) 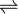        2Ag⁺ _(aq)     +    CrO₄^2-_(aq)

Let the solubility be S

Ag₂CrO_4(s) 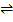   2 Ag⁺ _(aq) + CrO₄^2-_(aq)

          S                   2S               S

From Ksp = [Ag⁺] ² [CrO₄²⁺]

2.4 x 10 ^-12    = (2S) ²

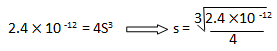
S = 8.434 x 10 ^-5 mol L^-1

 Example 2
Calculate the solubility of CaF₂ in water at 25^oC if its solubility product is 1.7 x 10 ^-10 M³

Solution
CaF₂
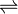    Ca ²⁺    +    2F ^–

   S              S              2S

Ksp = [Ca²⁺] [F^–] ²

             =S (2S) ²

1.7 x 10 ^-10    =   4S³

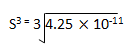
S = 3.489 x 10^-4 mol L^–

SOLUBILITY AND COMMON ION EFFECT

The solubility of sparingly soluble salts is lowered by the presence of second solute that furnishes (produce) common ions. Since the concentration of the common ion is higher than the equilibrium concentration, some ions will combine to restore the equilibrium (Le Chatelier’s principle)

Example 1
In solubility equilibrium of CaF₂, adding either Calcium ions or F^– ions will shift the equilibrium to the left reducing the solubility of CaF_2.

i.   Find the molar solubility of CaF₂ (Ksp = 3.9 x 10 ^-11 M³) in a solution containing 0.01M Ca(NO₃)₂          

Solution

Since Ca(NO₃)₂ is strong electrolyte, it will dissociates completely according to the equation.

Ca (NO₃)_{2 (s)}      Ca²⁺ _(aq)      +     2NO_3(aq)

0.01                            0.01             2(0.01)

CaF_2(s)              Ca²⁺_(aq)           +        2F^–_(aq)

  S                        S                        2S

Letting solubility of CaF₂ be S  

       CaF_2(s)              Ca²⁺ _(aq)   +      2F^–_(aq)

         S                     S             2S

                               0.01

From Ca (NO₃)₂     

In absence of   Ca(NO₃)₂

Ksp = [Ca²⁺] [F^–]²

3.9 x 10 ^-11   = S (2S) ²

3.9 x 10 ^-11   = 4S ³

S ³ = 9.75 x 10 ^-12

S = 2.136 x 10 ^-4 molL^-1

Assume the concentration of Ca²⁺ from Ca (NO₃)₂ does not affect the solubility of CaF₂ then concentration of Ca²⁺ will be 

[Ca²⁺]  = S + 0.01

              = (2.136 x 10^-4) + 0.01

  0.0102 M   ≈ 0.01

Since the Ksp value is very small, the expression 0.01 + S is approximated to 0.01

Ksp = [Ca²⁺] [F^–]²

3.9 x 10 ^-11 = 0.01 (2S) ²

3.9 x 10 ^-11   = 0.04S²

S² = 9.75 x 10 ^-10

S = 3.122 x 10 ^-5 mol/l

Conclusion
Hence, because of common ions effect, the solubility of CaF₂ has reduced from 2.13 x 10 ^-4 M to 3.122 x 10 ^-5 M

Example 2
Calculate the mass of PbBr₂ which dissolves in 1 litre of 0.1M hydrobromic acid (HBr) at 25^oC
(Ksp for PbBr₂ at 25^oC is 3.9 x 10 ^-8 M³) (Pb = 207, Br = 80)

Solution

PbBr₂ 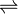      Pb²⁺    +         2Br^—

  S                  S                  2S

0.1  After adding HBr

At equilibrium

PbBr₂ 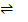   Pb²⁺    +  2Br

  S                 S       2S + 0.1

2S + 0.1     = 0.1      since Ksp is very small

Ksp   = [Pb²⁺][Br^–]²

3.9 x 10 ^-8   =   S (0.1)²

S = 3.9 x 10 ^-6 moll^-1

   

    

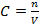
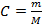
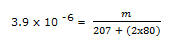
m = 1.43 x 10 ^-3 gl^-1 of PbBr₂

 Example 3
The solubility product of BaSO₄ in water is 10 ^-10 mol²l^-2 at 25^oC
(a) Calculate the solubility in water in moldm^-3

(b) 0.1 M of Na₂SO₄ solution is added to a saturated solution of BaSO₄. What is the solubility of BaSO₄ now?

Example 4

 Calculate the molar solubility of Mg (OH) ₂ in

(a) Pure water

(b) 0.05M MgBr₂

(c) 0.17 M KOH

(Ksp for Mg(OH)₂ is 7.943 x 10 ^-12 M³)

 (a)Solution

BaSO_{4 (s)}      Ba²⁺_(aq)    +      SO₄^2-_(aq)

S                      S                 S

10^-10mol²l^-2 = [Ba²⁺]  [SO₄^-2]

10^-10mol²l^-2 = S²

S = 1x 10 ^-5 mol/dm³

 (b) Solution

Na₂SO_4(s)       2Na⁺_(aq)   +         SO₄^2-_(aq)

0.1                       2 x 0.1=0.2        0.1

 BaSO_4
(s)           Ba²⁺_(aq)    +    SO₄
^2-_(aq)

S                            S                   S + 0.1                                     after adding Na₂SO₄

S + 0.1 ≈ 0.1 Ksp is very small

Ksp = [Ba²⁺][SO₄^2-]

1 x 10 ^-4 mol2/l²   =   S (0.1)

S = 1 x 10 ^-19 mol l^-1

S = 1 x 10 ^-9 mol l^-1

The value of S has reduced after adding NaSO₄

 4.  (a) Solution

Mg(OH)_2(aq) 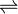        Mg²⁺_(aq)    +   2OH^–_(aq)

S                          S                     2S

Ksp = [Mg^2+][OH^-]2

7.943 x 10 ^-12   =   4S³

S³ = 1.985 x 10 ^-12

S = 1.25 x 10 ^-4 moll^-1

(b) Solution
KOH_(aq) 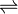           K⁺
_(aq)    +                OH^–_(aq)

0.17                      0.17                        0.17

Mg(OH)₂ 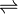     Mg²⁺      +   2OH^–

S                       S                 2S

                                            2S + 0.17

                                            2S + 0.17 = 0.17 Ksp is very small

Ksp =[Mg²⁺][OH^–]²

7.943 x 10 ^-12 M³   = S(0.17)²

S = 2.748 x 10 ^-10 moll^-1

 (c) Solution

MgBr₂ 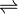       Mg²⁺         +      2Br^–

0.05                0.05              2 x 0.05 ≈ 0.1

Mg (OH)₂ 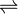          Mg²⁺          +             2OH^–

S                           S + 0.05     2S

S + 0.05   0.05    Ksp is very small

Ksp  =  [Mg²⁺][OH^–]²

7.943 x 10 ^-12 M³ = (0.05)(2S)²

S² = 3.9715 x 10 ^-11

S = 6.3 x 10 ^-6 moll^–