Form 5 Chemistry – PHYSICAL CHEMISTRY – Gases

DALTON’S LAW OF PARTIAL PRESSURE
It state that
” The total pressure of gases which are not reacting is equal to the sum of pressure of individual gases in a container”
Consider the two gases which are;
Gas A and Gas B
Each gas will create its own pressure.
Therefore the pressure of gases will be,
P_A for gas A
P_B for gas B
From Dalton’s  law of partial pressure,
P_T = P_A + P_B
Where by
PT is the total pressure of all gases in the container.

DEDUCTION OF DALTON’S  LAW OF PARTIAL PRESSURE FROM KINETIC THEORY OF GASES
From Dalton’s law for gas A and B
P_T = P_A + P_B
From kinetic theory of gases
PV = Nm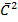
Since the volume is common.
For gas A
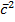P_AV = N_Am_A A
Since the volume is common.
For gas B
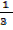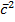P_BV = N_Bm_B B

If  P_t is the total pressure
V is the common volume
N_t is the total number of molecules
M  is the total mass of molecules
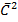is the sum of 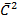of A and B
P_tV= N_t m
N_t =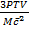

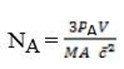
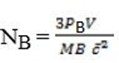
But N_t = N_A + N_B

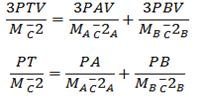
Since K. E is conserved ( It is the same before and after )
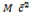= M_A
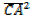= M_B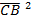
P_T = P_A + P_B,   Hence Dalton law deduced

QUESTION
Deduced the Avogadro’s law from kinetic theory of gases

THE IDEAL GAS EQUATION
This is the equation which is obeyed by all ideal gases.

Formulation of ideal gas equation
The ideal gas equation is formed from the combination of two gas law . These are
i) Charles’s law
ii) Boyle’s law

i)  Charle’s law
V 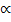T

ii)  Boyle’s law
V

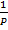
Combining

V

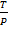
V =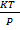

V = kT

k  represent universal gas constant which is denoted by R.

PV = RT
This is exactly for one mole of a gas.
For n moles of the gas
PV = nRT
Where
P is the pressure of the gas
V is the volume of the gas
n is the number of the moles of the gas
R is the universal constant
T is the absolute temperature

Units for R
R can be written as;
i)  R = 0.0821 atm moles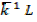
ii)  R = 8.314 ^-1 mol ^-1
Some questions  need  just general gas equation.
Recall

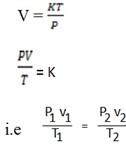
DEVIATION OF REAL GASES FROM IDEAL BEHAVIOUR
From kinetic theory of gases it has been observed that gases which do obey all assumption are termed as ideal gases.
For an ideal gas PV is exactly = 1
PV = nRT
For one mole of a gas.
PV = RT
The ratio of PV to RT is exactly 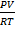1.0
= 1.0
Real gases do deviate from this behaviour at high pressure and low pressure.Therefore the variation of pressure cause the fluctuation on the value of    and this bring about the deviation of real gases from ideal behaviour. This deviation is graphically represent when the graph of   v/s  Pressure is plotted.
The graph of 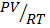            v/s   P (Amagat curve)

TERMS

• Critical temperature

 

edu.uptymez.com

It is the temperature above which the gas cannot be liquified  without further cooling.

• Critical pressure

 

edu.uptymez.com

It is the pressure at which the gas start to liquefy.

APPLICATION OF IDEAL GAS EQUATION
Ideal gas equation is applied in the following aspects;
1. Determination of moral mass of the gas.
From ideal gas equation
PV = nRT
But,  n is the number of moles
n =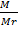
PV = 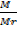RT ×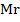

=
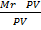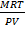
Mr  =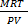 

Example 1
a) Define the following terms
i) Critical pressure
ii) Ideal gas
iii) Real gas
iv) Critical temperature
b) “Some gases are ideal while other are not
c) 1.27 of sample of oxide of nitrogen believed  to be either NO or NO₂  occupy the volume of 1.07 dm³ at 25⁰c and pressure of 737 mmHg.  Explain what oxide is it and why? R = 0.0821 atm mol ^-1 k ^-1 L.

Solution
Mass = 1. 27g
Volume = 1.07 dm³
Temperature = 737 mmHg
R = 0.0821
Unit conversion
1 dm³ = 1.0 L
T = 273 + 25 = 298k
1 atm = 760 mmHg
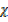= 0.97 atm
Mr =
Mr =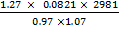
Mr = 29.9g/mol

Theoretical molar mass

NO₂ = 14 + 32 = 46

NO = 30

∴  The gas is NO because the molar mass is 30 g/mol.

2.  Determination of densities of gaseous materials
From ideal gas equation

PV = nRT

But n =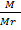

PV = RT

Mr =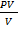

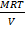
MrP =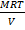

But, =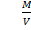 

Example 1
At what temperature would the oxygen gas be if the pressure is kept constant at 745 mmHg . If the density of the gas is 1.00g/dm^3. Given that
R is 0.0821 atm mol ^-1 k^-1 L

Solution
From O₂

Mr = ^.32
Pressure = 745
R = 0.0821
Density = 1.00g/dm³
T = ?
 = 

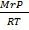
T  =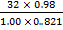 

= 381.9k
.^..  The temperature required = 381.9k

Example 2
What is the volume occupied by 13.7g of chlorine gas at 45^oc and 745 mmHg
R = 0.0821 atom mol^-1 k^-1 L

Solution
M = 13.7g
T = 45^oc
P = 745mmHg
R = 0.0821
Mr = 71

Conversion of units

T = 45 + 273 = 318K

P = 1 atm = 760mmHg

T = 745

P = 0.98 atm

From
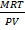
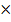PV Mr = PV

=

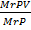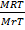
V =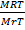

V =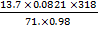

V = 5.14 Liters
∴  The volume of chlorine gas is 5.14dm³